小世界模型简介

小世界模型

“小世界现象”源于社会心理学家Stanley Milgram在20世纪60年代所做的试验。Milgram设计了一个实验，他在美国内布拉斯加州奥马哈市或者堪萨斯州戚奇托市，随机选取了一些用户，给在波士顿的日标用户送信。 只 有送信者和收信者之间非常熟悉才能直接将信送出。否则，送信者需要把信先发给那些有可能熟 知目标用户的人。 结果表明，这些信平均经过**5.5~6次**转手才能最终到达波士顿的目标用户手中。

提出的原因：

随机图模型正确模拟真实世界网络中的平均路径长度，但是低估了聚类系数。

为解决这个问题，Duncan J. Watts和Steven Strogatz 于1998年提出了小世界模型。

Watts D J , Strogatz S H . Collective dynamics of ‘small-world’ networks[J]. Nature, 1998.

小世界模型时介于规则格和随机图之间的一种模型，我们先来看一下规则格。

规则格的概念：

我们假设真实世界网络中有一个平等的模型，其中人们有相同数量的邻居(朋友)。

这显然也不现实，但可以更准确地模拟真实世界网络中的聚类系数。
在图理论中，这个假设等同于在一个规则网络中模拟这些个体。

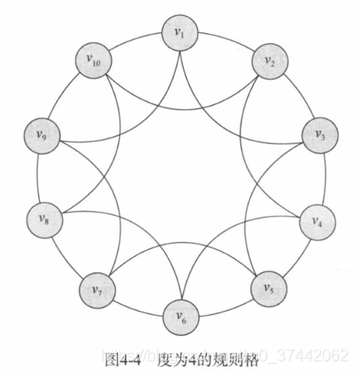
规则格是规则网络的一种特殊形式，其中存在着一种特殊的规则对具有连接关系的结点进行排序。
在一个度是?的规则格中，结点与它们的前?/?个邻居和后?/?个邻居进行连接。
形式上，对于结点集合?={?_?,?_?,?_?,…,?_?}，边存在于结点?_?和?_?之间，当且仅当?≤???(?−|(?−|?−?|,|?−?|)|)≤?/?.

缺点：
1.平均路径长度太长（约为?/??);
2.聚类系数约为3/4，定值，不能根据真实网络世界的聚