差错检测 — 循环冗余校验CRC

　　现实中通信链路都不会是理想的，比特在传输的过程中可能会出现差错，1可能变成0，0也可能变成1，这就叫做比特差错。比特差错是传输差错的一种，因此为了保证数据传输的可靠性，在计算网络传输数据时，必须采用各种检验措施来处理比特差错。目前在数据链路层广泛使用了循环冗余的CRC的检错技术。

• 帧检验序列FCS（Frame Check Sequence）：为了进行差错检验而添加的冗余码。
• 模2运算：即按位异或运算，不考虑进位与借位，相同为0，不同为1（做除法时每一步余数的首位逢一商一 逢零商零）
• 发送方和接收方事先商定的长度为（n+1）位的除数P，用多项式 P(x) 表示更为方便，又称生成多项式。
• 由（k-1）次多项式表示的 k 位比特消息 M(X)，每一比特位的值为 对应其每项多项式的系数，且从为高位比特开始。如一个8比特10011010对应的多项式为 M(x)=x^7 +x^4 +x^3 +x^1。
• n位冗余码：用二进制的模2运算进行2^n乘以M 的运算，相当于在M的后面添加n个0。

循环冗余检验的原理：在发送端，先把数据划分成组，假定每组k个比特并作为M，CRC运算就是在数据M的后面添加供差错检测用的n位冗余码，然后构成一个帧（k+n）位 并发送出去。将得到的（k+n）位的数除以收发双方事先商定的（n+1）位的除数P，得出的商是Q，而余数是R（n位，比P少一位）。在接收端把接受到的数据以帧为单位进行CRC检验：即把收到的每一个帧都除以P（模2运算），然后检查得到的余数R，如果传输无差错，那么R肯定是0，就接受；如果R≠0，则判定这个帧有差错（无法确定是哪几位出现差错），就丢弃。

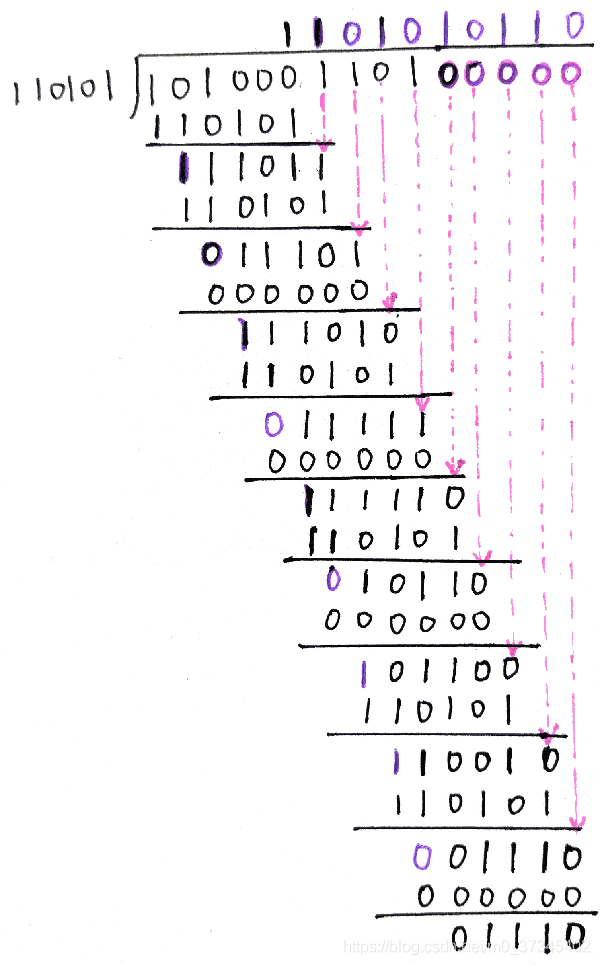
有效信息为1010001101，生成多项式p(x)=110101 , 求其CRC编码? 

答：如图所示（模2运算）

余数为01110，CRC编码为101000110101110