opengl 球体

理论：球的参数方程

https://baike.baidu.com/item/%E7%90%83%E9%9D%A2/5889102?fr=aladdin

不过我这里是y 与z的参数方程交换了关系式。即y=Rcos(φ)，注意我这里代码没有实现计算法向量数组，如果后期我用到了再加。（个人笔记，不喜勿喷）

效果：

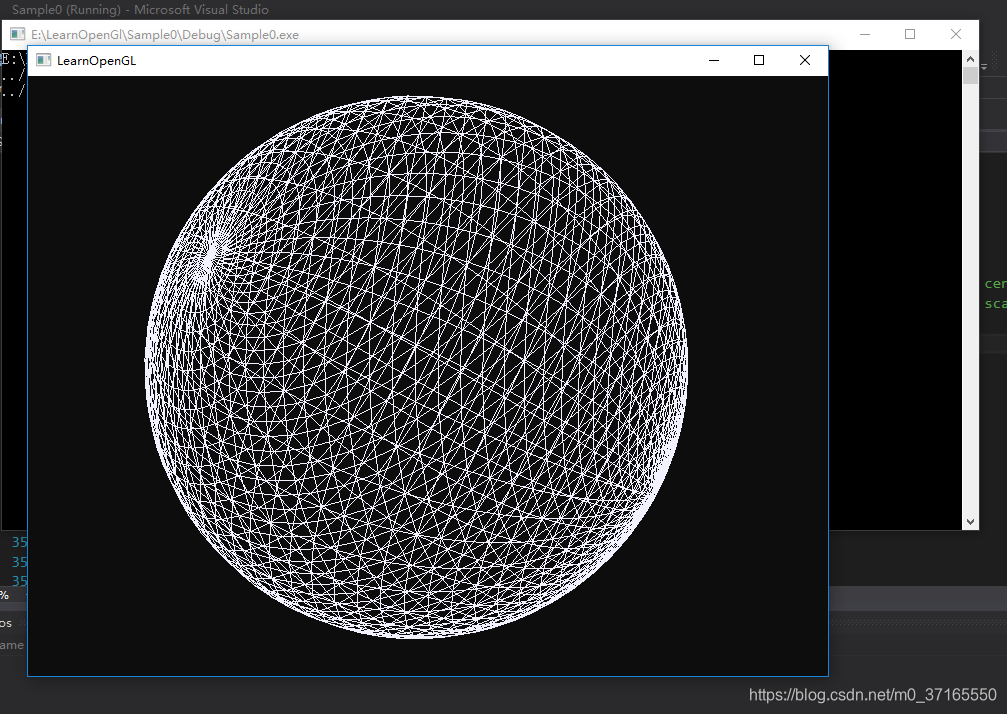
 画球代码：

int H=40, V=40;//H x-z平面圆分成多少份，V是y轴分成多少份 
const float PI = 3.141592653;
float HR =2*PI / H;
float VR = PI / V;

float R = 0.5;   //圆半径
int vSize = (V - 1)*H + 2;    //顶点数量
int indexSize = (2 * (V - 2)*H + 2 * H) * 3;//索引 ，glDrawElements使用

struct VertexM
{
	float X;
	float Y;
	float Z;
};


vector<VertexM> vertexs;//顶点数组
vector<unsigned int> indexs; //索引 ，glDrawElements使用

void drawSphere() {
	vertexs.clear();
	indexs.clear();

	for (size_t i = 0; i <= V; i++)
	{
		if (i==0)
		{
			VertexM vertex;
			vertex.X = 0;
			vertex.Y = R;
			vertex.Z = 0;
			vertexs.push_back(vertex);
			continue;
		}
		else if (i==V)
		{
			VertexM vertex;
			vertex.X = 0;
			vertex.Y = -R;
			vertex.Z = 0;
			vertexs.push_back(vertex);

			for (int t = H-1; t>=0 ; t--)
			{
				//球次最后各顶点与最后一个顶点的三角形索引
				indexs.push_back(vSize - 1);
				unsigned int temIndex = ((i - 2) * H + 1 + t);
				indexs.push_back(temIndex);

				if (t == 0)
				{
					indexs.push_back(temIndex + H - 1);
				}
				else
				{
					indexs.push_back(temIndex - 1);
				}
			
			}

			continue;
		}
	
		float theta = VR*i;
		for (size_t j = 0; j < H; j++)
		{
			float temX, temY, temZ,beta;
			beta = HR*j;
		
			temX = R*sin(theta)*sin(beta);
			temY = R*cos(theta);
			temZ = R*sin(theta)*cos(beta);


			VertexM vertex;
			vertex.X = temX;
			vertex.Y = temY;
			vertex.Z = temZ;

			vertexs.push_back(vertex);


			//index
			if (i==1)
			{
				indexs.push_back(0);
				indexs.push_back(j + 1);
				if (j==H-1)
				{
				 indexs.push_back(1);
				}
				else
				{
					indexs.push_back(j + 2);
				}
			}
			else
			{
				//三角形1
				unsigned int tem1 = H*(i - 2) + 1 + j;
				unsigned int tem2 = H*(i - 1) + 1 + j;
				unsigned int tem3 = H*(i - 2) + 2 + j;
				unsigned int tem4 = H*(i - 2) + 1;

				indexs.push_back(tem1);
				indexs.push_back(tem2);
				if (j == H - 1)
				{
					indexs.push_back(tem4);
				}
				else
				{
					indexs.push_back(tem3);
				}
				//三角形2
				unsigned int tem5 = tem2;
				unsigned int tem6 = H*(i - 1) + 2 + j;
				unsigned int tem7 = tem3;
				unsigned int tem8 = H*(i - 1) + 1;
				unsigned int tem9 = H*(i - 2) + 1;

				indexs.push_back(tem5);

				if (j == H - 1)
				{
					indexs.push_back(tem8);
					indexs.push_back(tem9);
				}
				else
				{
					indexs.push_back(tem6);
					indexs.push_back(tem7);
				}

			}
		
		}
	}
	unsigned int ad1 = vertexs.size();
	unsigned int ad2= indexs.size();
}

 VA0,VB0,EBO:

unsigned VAO, VBO, EBO;
	glGenVertexArrays(1,&VAO);
	glBindVertexArray(VAO);
	glGenBuffers(1,&VBO);
	glBindBuffer(GL_ARRAY_BUFFER,VBO);
	glBufferData(GL_ARRAY_BUFFER,vertexs.size()* sizeof(VertexM),&vertexs[0],GL_STATIC_DRAW);
	glGenBuffers(1,&EBO);
	glBindBuffer(GL_ELEMENT_ARRAY_BUFFER,EBO);
	glBufferData(GL_ELEMENT_ARRAY_BUFFER,indexs.size()* sizeof(unsigned int),&indexs[0],GL_STATIC_DRAW);
	glVertexAttribPointer(0,3,GL_FLOAT,GL_FALSE,3*sizeof(float),(void*)0);
	glEnableVertexAttribArray(0);
	glBindBuffer(GL_ARRAY_BUFFER,0);
	glBindVertexArray(0);

draw:

        glBindVertexArray(VAO);
		glDrawElements(GL_TRIANGLE_STRIP, indexSize, GL_UNSIGNED_INT, 0);
		glBindVertexArray(0);