1.小批量梯度下降mini-batch
1.1 概念
- 小批量梯度下降,顾名思义,指的是:
- 假如有一个训练集,大小为1,000,000,每次运行梯度下降,都需要整体遍历一遍数据集之后才能够运行一步。
- 小批量梯度下降,则将这一百万个样本,分成多份,每1000个样本(可以是其他数字)成为一个小批量。每次运行一个小批量样本时,梯度更新一次。那么,遍历整体一百万个样本时,梯度会更新1000次,即走1000步。
- 小批量维度:
Xt∈(Xn,1000)X^{t}∈(X_n,1000)Xt∈(Xn,1000)
Yt∈(1,1000)Y^t ∈ (1,1000)Yt∈(1,1000)

1.2 常用小批量份数
- 一般来说,当样本数量 ≤≤≤ 2000时,直接采用梯度下降算法
- 当样本数量$>$2000时,采取小批量梯度下降
- 每一组的样本数可以分为: 64,128,256,51264,128,256,51264,128,256,512等等,都是以2的幂次方为准
- 所有的X{t} Y{t}都是要放在CPU/GPU中的,这和你的配置,以及一个训练样本的大小都有关系,但是如果你使用的mini-batch超过了 CPU/GPU 内存的容量,不管你怎么做 你都会发现,结果会突然变得很糟 。
1.3 执行过程
和梯度下降类似,只不过梯度下降的X变成了X{t}。
repeat (for i = 1 to m/mtm/m_tm/mt):
前向传播→→→计算Z,A值→→→反向传播→→→计算梯度→→→更新梯度。
1.4 噪声影响
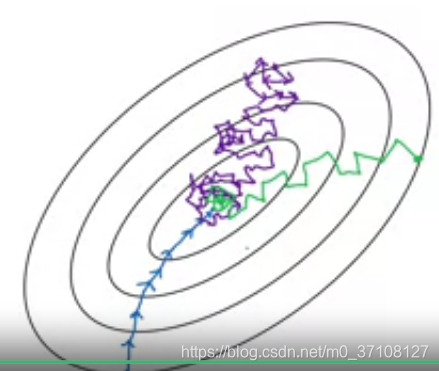
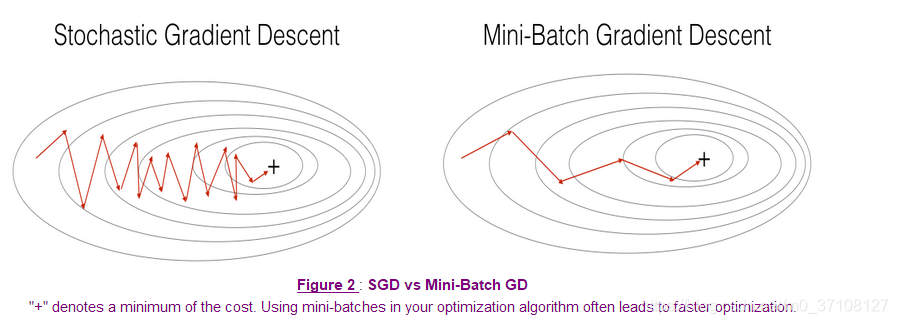
- 小批量梯度会产生噪声影响,因此会沿着一条弯弯扭扭的线条往最优化中心(最低点)移动。
- 同时,小批量梯度(绿色)和随机批量梯度(紫色,一个样本为一个mini-batch)都不会直接在中心停留,而是在周围不断徘徊。
2.指数加权平均
2.1 概念
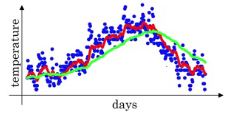
以温度为例。
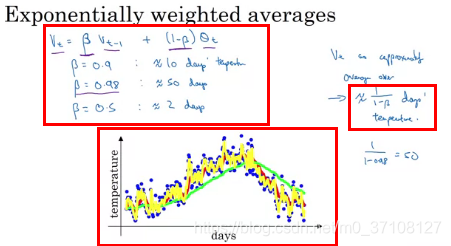
公式:Vt=βVt−1+(1−β)θtV_t=βV_{t-1} + (1-β)θ_tVt=βVt−1+(1−β)θt
≈1/(1−β)天的平均气温≈1/(1-β) 天的平均气温≈1/(1−β)天的平均气温
- 减少β会给画图的曲线增加噪音(因为以前的权值变小,最新的权值变大,导致曲线变动会更加及时,参照10天温度平均值)
- 增加β会让曲线向右移动,并且更平滑(因为以前的权值变大,最新的权值变小,曲线变动会比较缓慢,也就是很久之后才生效,参照50天温度平均值)
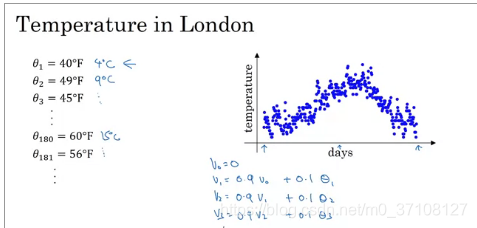
红色是以10天的平均温度画的曲线
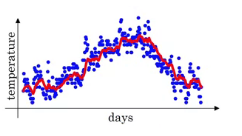
绿色的是以50天的平均温度画的曲线。更加平滑,并且向右移动。
这是因为以50天平均温度时,β取的0.98,那么由公式来看,则会以Vt−1V_{t-1}Vt−1为主,那么温度的即时变化则会反应的相对较慢。
黄色的是以2天平均温度画的曲线。
2.2 代码
代码比较高效,只用一个初始化值和一行代码即可给出平均值(其他算法给的平均值更准确,但是没有这个高效)。
Vθ=0V_θ = 0Vθ=0
repeat:
Vθ:=βV+(1−β)θtV_θ := βV + (1-β)θ_tVθ:=βV+(1−β)θt
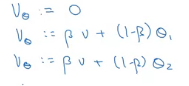
2.3 偏差修正
即用 Vt(1−βt)\frac{V_t}{(1-β^t)}(1−βt)








 本文详细介绍了深度学习中改善神经网络超参数的方法,包括小批量梯度下降的概念、常用小批量份数及其影响,动量梯度下降、RMSprop及Adam优化算法的原理和使用方法。此外,还讨论了学习速率衰减的概念和策略。
本文详细介绍了深度学习中改善神经网络超参数的方法,包括小批量梯度下降的概念、常用小批量份数及其影响,动量梯度下降、RMSprop及Adam优化算法的原理和使用方法。此外,还讨论了学习速率衰减的概念和策略。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章
















 929
929

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








