[C++ 学习笔记] 二叉搜索树-BST_c++ bst 求排名-优快云博客

本文链接：https://blog.youkuaiyun.com/lzl20220405/article/details/135141891

1. 基本知识

BST(Binary Search Tree)，二叉搜索树，又叫二叉排序树，是一棵空树或满足以下几种性质的树

若左子树不空，则左子树上所有节点的值均小于根节点的值
若右子树不空，则右子树上所有节点的值均大于根节点的值
左、右子树也分别为二叉搜索树
没有权值相等的节点

对于任一棵非空二叉搜索树，容易发现，其中序遍历单调递增

2. 初始化二叉搜索树

一般二叉搜索树的一个节点有如下属性：

当前节点的权值
左孩子的下标
右孩子的下标
计数器，代表当前的值出现了几次
子树大小（包括自己） => 这个属性用来求节点的 “排名”

于是可以得到节点的代码：

struct Node{
    int val;    // 权值
    int lhs;    // 左孩子下标
    int rhs;    // 右孩子下标
    int cnt;    // 计数器
    int siz;    // 子树大小
}BST[1000005];

3. 添加节点

对于要添加的节点的值 (不妨设为 $val$ )，按照以下的步骤添加节点：

比较 $val$ 与当前节点的值
如果 $val$ > 当前节点的值，则搜索当前节点的右子树（若没有右子树就直接赋为右孩子）
如果 $val$ < 当前节点的值，则搜索当前节点的左子树（若没有左子树就直接赋为左孩子）

图例：

目标：将权值为 4 的点插入到给出的二叉搜索树中

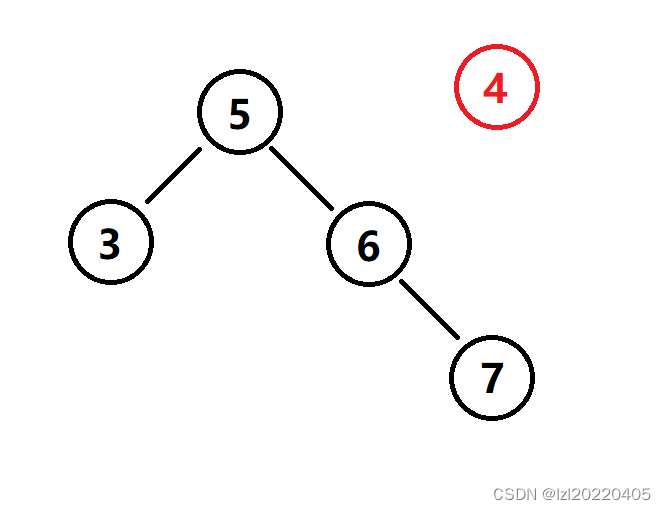
1. 将 4 与根节点的值 5 比较，发现 4<5，于是搜索其左子树

2. 将 4 与左子树的根节点的值 3 比较，发现 4>3，于是搜索其右子树

3. 发现当前节点没有右子树，于是将其右子树指向要插入的节点

插入完毕！

于是可以得到插入的代码：

void insert_node(int val, int pos) {    // 要插入节点的权值，当前递归到的节点的位置
	BST[pos].siz++;    // 查到了这个节点，说明这个节点的子树包含要插入的节点，因此 siz++

	if (BST[pos].val == val) {    // 如果节点已经存在，则 cnt++
		BST[pos].cnt++;
		return;
	}

	if (BST[pos].val < val) {    // 如果要插入的权值大于当前节点权值，向右子树搜索
		if (BST[pos].rhs == 0) {    // 没有右子树，则直接让右子树指向新节点
			recent_pos++;    // recent_pos 指当前一共有多少个节点
			BST[recent_pos].cnt = 1;
			BST[recent_pos].siz = 1;
			BST[recent_pos].val = val;
			BST[pos].rhs = recent_pos;
			return;
		}

		insert_node(val, BST[pos].rhs);    // 递归右子树
	} else {    // 如果要插入的权值小于当前节点权值，向左子树搜索
		if (BST[pos].lhs == 0) {    // 没有左子树，则直接让左子树指向新节点
			recent_pos++;
			BST[recent_pos].cnt = 1;
			BST[recent_pos].siz = 1;
			BST[recent_pos].val = val;
			BST[pos].lhs = recent_pos;
			return;
		}

		insert_node(val, BST[pos].lhs);    // 递归左子树
	}
}

4. 找给定权值的前驱

前驱定义为，小于当前权值且最大的数

大体思路与插入相同，具体注释可以看代码：

int find_pre(int val, int pos, int ans) {    // 要找前驱的权值，当前节点的下标，当前找到的比 val 小的最大值
	if (BST[pos].val >= val) {    // 如果当前节点权值大于 val，则向左子树寻找
		if (BST[pos].lhs == 0) {    // 若当前节点没有左子树，说明在当前节点的子树上没有比 val 更小的数了，那么当前 ans 即为答案，直接返回找到的 ans
			return ans;
		}

		return find_pre(val, BST[pos].lhs, ans);    // 若当前节点有左子树，则向左子树寻找
	}

    // 如果当前节点权值小于 val, 则向右子树寻找

	if (BST[pos].rhs == 0) {    // 若当前节点没有右子树，说明当前节点的子树上没有节点的权值 大于当前节点 且 小于要找前驱的权值，那么当前节点即为答案，直接返回当前节点的权值
		return BST[pos].val;
	}

	return find_pre(val, BST[pos].rhs, BST[pos].val);    // 若当前节点有右子树，则向右子树寻找
}

5. 找给定权值的后继

后继定义为，大于当前权值且最小的数

大体思路与找前驱相同，具体注释可以看代码：

int find_nxt(int val, int pos, int ans) {    // 要找后继的权值，当前节点的下标，当前找到的比 val 大的最小值
	if (BST[pos].val <= val) {    // 如果当前节点权值小于 val，则向右子树寻找
		if (BST[pos].rhs == 0) {    // 若当前节点没有右子树，说明在当前节点的子树上没有比 val 更大的节点了，那么先前找到的 ans 即为答案，直接返回 ans
			return ans;
		}

		return find_nxt(val, BST[pos].rhs, ans);    // 若当前节点有右子树，则向右子树寻找
	}
   
    // 如果当前节点权值大于 val，则向左子树寻找

	if (BST[pos].lhs == 0) {    // 若当前节点没有左子树，说明在当前节点的子树上没有满足 大于val 且 小于当前节点权值 的节点了，那么当前节点权值即为答案，直接返回当前节点权值    
		return BST[pos].val;    
	}

	return find_nxt(val, BST[pos].lhs, BST[pos].val);    // 若当前节点有左子树，则向左子树寻找
}

6. 找给定权值的排名

排名定义为，比当前权值小的权值的个数 +1（注意重复的也算哦）

因此，找排名就是找比当前节点权值小的权值的个数

那么，我们可以整理出大致的思路：

如果当前节点的权值大于要找排名的权值，那么往当前节点的左子树上找
如果当前节点的权值等于要找排名的权值，那么容易发现，当前节点子树上所有小于当前节点权值的权值个数正好为当前节点左子树的大小，那么直接返回当前节点左子树的大小
如果当前节点的权值小于要找排名的权值，那么容易发现，当前节点的权值与当前节点左子树的所有节点的权值必然都小于要找排名的权值，且要找排名的权值必然在当前节点的右子树上，那么往当前节点的右子树上找，并将结果加上当前节点的出现次数以及当前节点左子树的大小

于是可以得到找排名的代码：

int val_find_rank(int val, int pos) {    // 要找排名的权值，当前节点的位置
	if (pos == 0) {    // 没有排名，即找到的是空节点
		return 0;
	}

	if (val == BST[pos].val) {   // 如果当前节点的权值 等于 要找排名的权值
		return BST[BST[pos].lhs].siz;    // 返回当前节点左子树的大小
	}

	if (val < BST[pos].val) {    // 如果当前节点的权值 大于 要找排名的权值
		return val_find_rank(val, BST[pos].lhs);    // 向当前节点的左子树找
	}

	// 如果当前节点的权值 小于 要找排名的权值
    // 向当前节点的右子树找，并将结果加上 当前节点的出现次数 与 当前节点左子树的大小

    return val_find_rank(val, BST[pos].rhs) + BST[BST[pos].lhs].siz + BST[pos].cnt;
}

7. 找给定排名的权值

容易发现，一个节点的左子树上节点的排名一定小于当前节点的排名

一个节点的右子树上节点的排名一定为其的排名+当前节点的出现次数+当前节点左子树的大小

那么，其实根据排名找权值的思路与根据权值找排名的思路大致相反：

如果当前节点左子树的大小 大于等于 要查找排名的大小，那么往当前节点的左子树搜索
如果当前节点左子树的大小加上当前节点的出现次数 大于等于 要查找排名的大小，那么当前节点即为要找的点，直接返回当前节点的值（在判断过步骤 1 的基础上）
如果当前节点左子树的大小加上当前节点的出现次数小于要查找排名的大小，那么往当前节点的右子树搜索，并将排名减去 (当前节点左子树的大小+当前节点的出现次数)

于是可以得到找权值的代码：

int rank_find_val(int rank, int pos) {
	if (pos == 0) {    // 如果找的点不存在
		return 2147483647;
	}

	if (BST[BST[pos].lhs].siz >= rank) {    // 如果当前节点左子树的大小 大于等于 要找的排名
		return rank_find_val(rank, BST[pos].lhs);    // 向当前节点的左子树搜索
	}

	if (BST[BST[pos].lhs].siz + BST[pos].cnt >= rank) {    // 如果当前节点左子树的大小 加上 当前节点的出现次数 大于等于 要找的排名
		return BST[pos].val;    // 直接返回当前节点的权值
	}

    // 否则，向右子树搜索，并将要查找的排名 减去 (当前节点左子树的大小+当前节点的出现次数)

	return rank_find_val(rank - BST[BST[pos].lhs].siz - BST[pos].cnt, BST[pos].rhs);
}