LA 4123

LA 4123 Glenbow Museum
题目链接：LA 4123
题目大意（摘自lrj的训练指南）：对于一个平行于坐标轴的多边形，我们可以用一个由R和O组成的序列来描述它，从某个顶点开始按照逆时针方向走，碰到一个90°的内角（也就是左转）记R，碰到一个270°的内角（右转）记O。将这样的序列称为角度序列。给定正整数L，问有多少长度为L的角度序列可以对应都少个星型多边形（即多边形中存在一点可以看到多边形边界上的所有点）。
题目分析：最容易想到的符合题意的多边形应该是下面这样的：
我们可以发现，如果我们把一个多边形分成四份，即左上，右上，左下和右下，每一部分都是由形如RORO……ROR的样式，因此在总共的序列中R比O一定多了4个。因此我们可以算出R共有（n+4）/2个，O共有（n-4）/2个。进一步我们发现序列中的O是不会相邻的，否则一定不会构成一个封闭图形，因此我们可以利用排列组合算出答案，先将R排好，然后将O插入到R形成的空中，共有（n+4）/2+1个空，然后再去掉首尾都是O的情况，最终答案为：

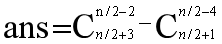
最后附上完整代码：

#include<stdio.h>
#include<algorithm>
#include<string.h>
#define LL long long
int n,Case,m;
LL ans;
LL cc(int a,int b){
	LL tmp=1;
    for(int i=a+1;i<=b;++i)
  		tmp*=i;
	tmp/=120;
    return tmp;
}
int main()
{
//	freopen("1.txt","r",stdin);
	while(scanf("%d",&n)){
		if(n==0)break;
		ans=0;
		ans=cc(n/2-2,n/2+3)-cc(n/2-4,n/2+1);
		if(n%2)printf("Case %d: 0\n",++Case);
		else printf("Case %d: %I64d\n",++Case,ans);
	}
	return 0;
 }