统计学习方法笔记与习题解答(Chapter7)(二)

支持向量机

SMO算法

问题描述

$$\begin{array}{rl}\underset{\alpha }{\min }& \frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_{j}K(x_i,x_j)-\sum _{i=1}^N{\alpha }_i\\ s.t.& \sum _{i=1}^N{\alpha }_i{y}_i=0\\ & 0⩽{\alpha }_i⩽C,i=1,2,\dots ,N\end{array}$$

这个问题中，变量是$\alpha$，一个变量${\alpha }_i$对应一个样本点$(x_i,y_i)$，变量总数等于$N$

KKT 条件

• KKT条件是该最优化问题的充分必要条件
• 简单来说，约束最优化问题包含$⩽0$，和$=0$两种约束条件
  $$\begin{array}{rl}\underset{x\in R^n}{\min }& f(x)\\ s.t.& c_i(x)⩽0,i=1,2,\dots ,k\\ & h_j(x)=0,j=1,2,\dots ,l\end{array}$$
• 引入广义拉格朗日函数

$$L(x,\alpha ,\beta )=f(x)+\sum _{i=0}^k{\alpha }_i{c}_i(x)+\sum _{j=1}^l{\beta }_j{h}_j(x)$$

• 在KKT的条件下，原始问题和对偶问题的最优值相等
  $$\begin{gathered} {\nabla }_{x}L(x^{\ast },{\alpha }^{\ast },{\beta }^{\ast })=0 \\ {\nabla }_{\alpha }L(x^{\ast },{\alpha }^{\ast },{\beta }^{\ast })=0 \\ {\nabla }_{\beta }L(x^{\ast },{\alpha }^{\ast },{\beta }^{\ast })=0 \\ {\alpha }_i^{\ast }{c}_i(x^{\ast })=0,i=1,2,\dots ,k \\ {c}_i(x^{\ast })\le 0,i=1,2,\dots ,k \\ {\alpha }_i^{\ast }\ge 0,i=1,2,\dots ,k \\ {h}_j(x^{\ast })=0,j=1,2,\dots ,l \end{gathered}$$
• 前面三个条件是由解析函数的知识，对于各个变量的偏导数为0，后面四个条件就是原始问题的约束条件以及拉格朗日乘子需要满足的约束,第四个条件是KKT的对偶互补条件

算法内容

整个SMO算法包括两部分：

1. 求解两个变量二次规划的解析方法
2. 选择变量的启发式方法

$$\begin{array}{rl}\underset{\alpha }{\min }& \frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_{j}K(x_i,x_j)-\sum _{i=1}^N{\alpha }_i\\ s.t.& \sum _{i=1}^N{\alpha }_i{y}_i=0\\ & 0⩽{\alpha }_i⩽C,i=1,2,\dots ,N\end{array}$$

Part I

• 两个变量二次规划求解
• 选择两个变量${\alpha }_1,{\alpha }_2$，由等式约束可以得到${\alpha }_1=-y_1\sum _{i=2}^N{\alpha }_i{y}_i$，所以这个问题等价于一个单变量优化问题

$$\begin{array}{rl}\underset{{\alpha }_1,{\alpha }_2}{\min }W({\alpha }_1,{\alpha }_2)=& \frac{1}{2}{K}_{11}{\alpha }_1^2+\frac{1}{2}{K}_{22}{\alpha }_2^2+y_1{y}_2{K}_{12}{\alpha }_1{\alpha }_2\\ & -({\alpha }_1+{\alpha }_2)+y_1{\alpha }_1\sum _{i=3}^N{y}_i{\alpha }_i{K}_{il}+y_2{\alpha }_2\sum _{i=3}^N{y}_i{\alpha }_i{K}_{i2}\\ s.t.& {\alpha }_1{y}_1+{\alpha }_2{y}_2=-\sum _{i=3}^N{y}_i{\alpha }_i=\varsigma \\ & 0⩽{\alpha }_i⩽C,i=1,2\end{array}$$

• 上面存在两个约束：

1. 线性等式约束
2. 边界约束

• 根据简单的线性规划可以得出等式约束使得$({\alpha }_1,{\alpha }_2)$在平行于盒子$[0,C]\times [0,C]$的对角线的直线上

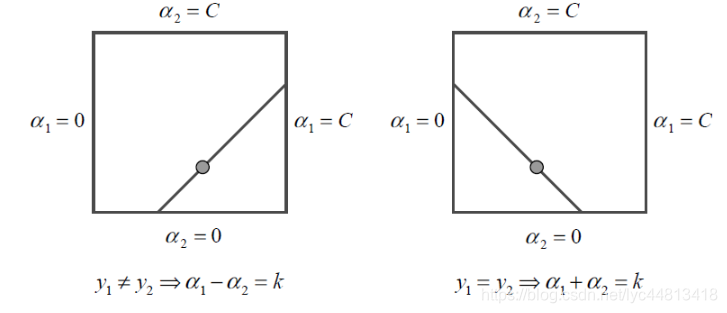
• 首先求沿着约束方向未经剪辑，即不考虑约束$0⩽{\alpha }_i⩽C$时${\alpha }_2$的最优解，然后再求剪辑后的解
  $$E_i=g(x_i)-y_i=(\sum _{j=1}^N{\alpha }_j{y}_{j}K(x_i,x_j)+b)-y_i,i=1,2$$
  $E_i$为函数$g(x)$对输入的预测值与真实输出$y_i$的差

Part II

• 变量的选择方法

1. 第一个变量${\alpha }_1$外层循环，寻找违反KKT条件最严重的样本点
2. 第二个变量${\alpha }_2$内层循环，希望能使${\alpha }_2$有足够大的变化
3. 计算阈值$b$和差值$E_i$

输入：训练数据集$T=(x_1,y_1),(x_2,y_2),\dots ,(x_N,y_N)$，其中 x i ∈ X = R n , y i ∈ Y = { − 1 , + 1 } , i = 1 , 2 , … , N x_i\in\mathcal X=\bf R^n, y_i\in\mathcal Y=\{-1,+1\}, i=1,2,\dots,N xi​∈X=Rn,yi​∈Y={−1,+1},i=1,2,…,N,精度$ϵ$

输出：近似解$\hat{\alpha }$

1. 取初值${\alpha }_0=0$，令$k=0$

2. 选取优化变量${\alpha }_1^{(k)},{\alpha }_2^{(k)}$，解析求解两个变量的最优化问题，求得最优解${\alpha }_1^{(k+1)},{\alpha }_2^{(k+1)}$，更新$\alpha$为${\alpha }^{k+1}$

3. 若在精度$ϵ$范围内满足停止条件
   ∑ i = 1 N α i y i = 0 0 ⩽ α i ⩽ C , i = 1 , 2 , … , N y i ⋅ g ( x i ) = { ⩾ 1 , { x i ∣ α i = 0 } = 1 , { x i ∣ 0 &lt; α i &lt; C } ⩽ 1 , { x i ∣ α i = C } g ( x i ) = ∑ j = 1 N α j y j K ( x j , x i ) + b \sum_{i=1}^{N}\alpha_iy_i=0\\ 0\leqslant\alpha_i\leqslant C,i=1,2,\dots,N\\ y_i\cdot g(x_i)= \begin{cases} \geqslant1,\{x_i|\alpha_i=0\}\\ =1,\{x_i|0&lt;\alpha_i&lt;C\}\\ \leqslant1,\{x_i|\alpha_i=C\} \end{cases}\\ g(x_i)=\sum_{j=1}^{N}\alpha_jy_jK(x_j,x_i)+b i=1∑N​αi​yi​=00⩽αi​⩽C,i=1,2,…,Nyi​⋅g(xi​)=⎩⎪⎨⎪⎧​⩾1,{xi​∣αi​=0}=1,{xi​∣0<αi​<C}⩽1,{xi​∣αi​=C}​g(xi​)=j=1∑N​αj​yj​K(xj​,xi​)+b
   则转4,否则，$k=k+1$转2

4. 取$\hat{\alpha }={\alpha }^{(k+1)}$

习题解答

• 1.比较感知机的对偶形式与线性可分支持向量机的对偶形式

  • 感知机的对偶形式
    $f(x)=sign\left({\sum }_{j=1}^N{\alpha }_j{y}_j{x}_j\cdot x+b\right),\alpha =({\alpha }_1,{\alpha }_2,\cdots ,{\alpha }_N{)}^T$
  • 线性可分支持向量机的对偶形式
    $f(x)=sign\left({\sum }_{i=1}^N{\alpha }_i^{\ast }{y}_i{x}_i\cdot x+b^{\ast }\right),{\alpha }^{\ast }=({\alpha }_1^{\ast },{\alpha }_2^{\ast },\cdots ,{\alpha }_N^{\ast }{)}^T$
    感知机学习算法的原始形式和对偶形式与线性可分支持向量机学习算法的原始形式和对偶形式相对应。在线性可分支持向量机的对偶形式中,$w$也是被表示为实例 $x_i$和标记$y_i$的线性组合的形式
    $$w=\sum _{i=1}^N{\alpha }_i{y}_i{x}_i$$
    而它们的偏置$b$的形式不同，前者$b={\sum }_{i=1}^N{\alpha }_i{y}_i$,而后者$b^{\ast }=y_j-{\sum }_{i=1}^N{\alpha }_i^{\ast }{y}_i(x_i\cdot x_j)$

• 2.已知正例点$x_1=(1,2{)}^T$，$x_2=(2,3{)}^T$，$x_3=(3,3{)}^T$,负例点$x_4=(2,1{)}^T$，$x_5=(3,2{)}^T$，
  试求最大间隔分离超平面和分类决策函数，并在图上画出分离超平面、间隔边界及支持向量

  • 根据书中算法，计算可得$w_1=-1$,$w_2=2$,$b=-2$,即最大间隔分离超平面为
    $$-x^{(1)}+2x^{(2)}-2=0$$
    分类决策函数为
    $$f(x)=sign(-x^{(1)}+2x^{(2)}-2)$$
    

• 3.线性支持向量机还可以定义为以下形式：

$$\begin{gathered} \underset{w,b,\xi }{\min }\frac{1}{2}\Vert w{\Vert }^2+C\sum _{i=1}^N{\xi }_i^2 \\ s.t.y_i(w\cdot x_i+b)\ge 1-{\xi }_i,i=1,2,\cdots ,N \\ {\xi }_i\ge 0,i=1,2,\cdots ,N \end{gathered}$$
试求其对偶形式

• 首先求得原始化最优问题的拉格朗日函数是：
  $L(w,b,\alpha ,\xi ,\mu )=\frac{1}{2}{\Vert w\Vert }^2+C{\sum }_{i=1}^N{\xi }_i^2-{\sum }_{i=1}^N{\alpha }_i(y_i(w\cdot x_i+b-1)+{\xi }_i)-{\sum }_{i=1}^N{\mu }_i{\xi }_i$
• 对偶问题是拉格朗日的极大极小问题。首先求$L(w,b,\alpha ,\xi ,\mu )$对$w,b,\xi$的极小,即对该三项求偏导，得
  $$\begin{gathered} w=\sum _{i=1}^N{\alpha }_i{y}_i{x}_i \\ \sum _{i=1}^N{\alpha }_i{y}_i=0 \\ 2C{\xi }_i-{\alpha }_i-{\mu }_i=0 \end{gathered}$$
  将上述带入拉格朗日函数，得
  $$\begin{gathered} -\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j(x_i\cdot x_j)-C\sum _{i=1}^N{\xi }_i^2+\sum _{i=1}^N{\alpha }_i \\ -\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j(x_i\cdot x_j)-\frac{1}{4C}\sum _{i=1}^N({\alpha }_i+{\mu }_i{)}^2+\sum _{i=1}^N{\alpha }_i \end{gathered}$$
• 4.证明内积的正整数幂函数$K(x,z)=(x\cdot z{)}^p$是正定核函数，这里$p$是正整数，$x,z\in R^n$

  • 要证明正整数幂函数是正定核函数，只需证明其对应得Gram矩阵$K=[K(x_i,x_j){]}_{m\times m}$是半正定矩阵

  • 对任意$c_1,c_2\dots c_m\in R$,有

    $$\begin{array}{rl}\sum _{i,j=1}^m{c}_i{c}_{j}K(x_i,x_j)& \\ =& \sum _{i,j=1}^m{c}_i{c}_j(x_i\cdot x_j{)}^p\\ =& (\sum _{i=1}^m{c}_i{x}_i)(\sum _{j=1}^m{c}_j{x}_j)(x_i{x}_j{)}^{p-1}\\ =& ||\sum _{i=1}^m{c}_i{x}_i|{|}^2(x_i{x}_j{)}^{p-1}\end{array}$$

    • 由于p大于等于1，该式子也大于等于0，即Gram矩阵半正定，所以正整数的幂函数是正定核函数