深度学习笔记

最新推荐文章于 2023-09-14 22:34:58 发布

老肥码码码

最新推荐文章于 2023-09-14 22:34:58 发布

阅读量952

点赞数 2

CC 4.0 BY-SA版权

分类专栏： MachineLearning

本文链接：https://blog.youkuaiyun.com/lyc44813418/article/details/89438990

MachineLearning 专栏收录该内容

15 篇文章

订阅专栏

神经网络

激活函数

sigmoid函数
- $σ(x)=1/(1+e^{-x})$
- 落伍原因：
  1.梯度饱和问题（sigmoid saturate and kill gradients），即如果神经元的激活值很大，返回的梯度几乎为零，因此反向传播的时候，也会阻断（or kill）从此处流动的梯度。此外初始化的时候，也要注意，如果梯度很大的话，也很容易造成梯度饱和。
  2.Sigmoid函数的输出不是零中心的（sigmoid outputs are not zero-centered），因为输出结果在 [0,1] 之间，都是整数，所以造成了某些维度一直更新正的梯度，某些则相反。就会造成 zig-zagging 形状的参数更新。不过利用 batch sgd 就会缓解这个问题，没有第一个问题严重。
- 代码实现

     import numpy as np
     def sigmoid(x):
         return 1 / (1 + np.exp(-x))

在这里插入图片描述

tanh函数
- $t a n h (x) = 2 σ (2 x) - 1$
- $tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$ 可以看作放大平移的sigmoid函数，值域为（-1，1）
- tanh non-linearity 虽然也有梯度饱和问题，但是起码是 zero-centered，因此实际中比 sigmoid 效果更好。
- 代码实现
```
    import numpy as np
    def tanh(x):
        return 2*sigmoid(2*x)-1 
```
ReLU函数
- Rectified Linear Unit，校正线性单元， f(x)=max(0,x)
- 优点1：相较于sigmoid和tanh函数，ReLU对于随机梯度下降的收敛有巨大的加速作用，这是由它的线性，非饱和的公式导致的
- 优点2：sigmoid和tanh神经元含有指数运算等耗费计算资源的操作，而ReLU可以简单地通过对一个矩阵进行阈值计算得到。
- 缺点：在训练的时候，ReLU单元比较脆弱并且可能“死掉”。举例来说，当一个很大的梯度流过ReLU的神经元的时候，可能会导致梯度更新到一种特别的状态，在这种状态下神经元将无法被其他任何数据点再次激活。通过合理设置学习率，这种情况的发生概率会降低。
- 代码实现

     import numpy as np
     def relu(x):
         return np.maximum(0, x)

在这里插入图片描述

Leaky ReLU函数
- 为了修复 “dying ReLU” 问题,该函数不是单纯的把负数置零，而是加一个很小的 slope，比如 0.01
- $f (x) = 1 (x < 0) (α x) + 1 (x \geq 0) (x)$
- 如果 α 作为参数，即每个神经元的 slope 都不一样，可以自学习的话，就是 PReLU
Maxout函数
- Maxout是对ReLU和leaky ReLU的一般化归纳.
- 它的函数是： $max(w_1^Tx+b_1,w_2^T+b_2)$
- ReLU和Leaky ReLU都是这个公式的特殊情况（比如ReLU就是w1=b1=0的时候）。这样Maxout神经元就拥有ReLU单元的所有优点（线性操作和不饱和），而没有它的缺点（死亡的ReLU单元）。
- 然而和ReLU对比，它每个神经元的参数数量增加了一倍，这就导致整体参数的数量激增。*

在实践中，用 ReLU 较多，学习率要调小一点，如果 dead units 很多的话，用 PReLU 或者 Maxout 试一下。

数据预处理

均值减法（Mean subtraction）
- 它对数据中每个独立特征减去平均值，在numpy中，该操作可以通过代码
  X -= np.mean(X, axis=0)实现。
- 而对于图像，更常用的是对所有像素都减去一个值，可以用 X -= np.mean(X) 实现，也可以在3个颜色通道上分别操作。
归一化（Normalization）
- 将数据的所有维度都归一化，使其数值范围都近似相等。有两种常用方法可以实现归一化。
- 第一种是先对数据做零中心化（zero-centered）处理，然后每个维度都除以其标准差，实现代码为 X /=np.std(X, axis=0) 。
- 第二种方法是对每个维度都做归一化，使得每个维度的最大和最小值是1和-1。
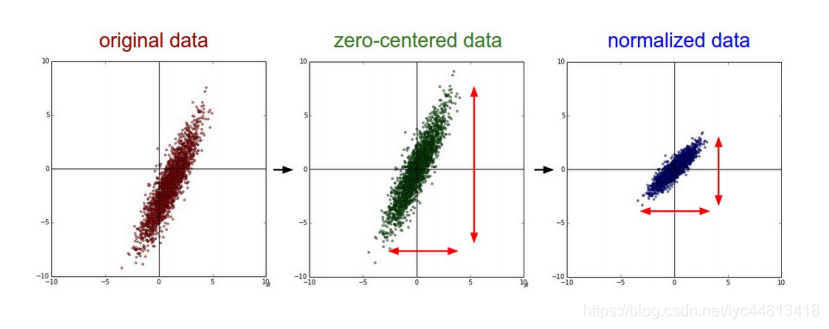
- 一般数据预处理流程：左边 :原始的2维输入数据。中间 :在每个维度上都减去平均值后得到零中心化数据，现在数据云是以原点为中心的。右边 : 每个维度都除以其标准差来调整其数值范围。红色的线指出了数据各维度的数值范围，在中间的零中心化数据的数值范围不同，但在右边归一化数据中数值范围相同。

PCA

先对数据进行零中心化处理，然后计算协方差矩阵，它展示了数据中的相关性结构

 #假设输入数据矩阵X的尺寸为[N x D]
 import numpy as np
 X ‐= np.mean(X, axis = 0) # 对数据进行零中心化(重要)
 cov = np.dot(X.T, X) / X.shape[0] # 得到数据的协方差矩阵
 U,S,V = np.linalg.svd(cov) #奇异值分解
 Xrot = np.dot(X,U) # 对数据去相关性
 Xrot_reduced = np.dot(X, U[:,:100]) # Xrot_reduced 变成 [N x 100]

通常使用PCA降维过的数据训练线性分类器和神经网络会达到非常好的性能效果，同时还能节省时间和存储器空间。

白化（whitening）
- 白化操作的输入是特征基准上的数据，然后对每个维度除以其特征值来对数值范围进行归一化。该变换的几何解释是：如果数据服从多变量的高斯分布，那么经过白化后，数据的分布将会是一个均值为零，且协方差相等的矩阵。

import numpy as np
# 对数据进行白化操作:
# 除以特征值
Xwhite = Xrot / np.sqrt(S + 1e‐5)

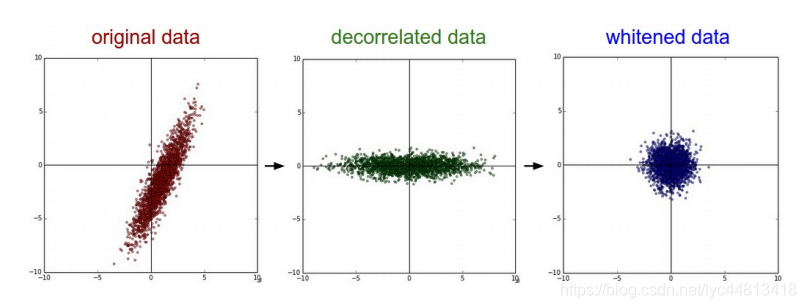
在这里插入图片描述

PCA/白化。左边是二维的原始数据。中间 : 经过PCA操作的数据。可以看出数据首先是零中心的，然后变换到了数据协方差矩阵的基准轴上。这样就对数据进行了解相关（协方差矩阵变成对角阵）。右边 : 每个维度都被特征值调整数值范围，将数据协方差矩阵变为单位矩阵。从几何上看，就是对数据在各个方向上拉伸压缩，使之变成服从高斯分布的一个数据点分布。
注意点：应该先分成训练/验证/测试集，只是从训练集中求图片平均值，然后各个集（训练/验证/测试集）中的图像再减去这个平均值。

输出层

神经网络可以用在分类问题和回归问题上，不过需要根据情况改变输出层的激活函数。一般而言，回归问题要用恒等函数，分类问题要用softmax函数。

softmax函数
- 该式在计算机的运算上有溢出问题，指数函数的值容易变得非常大，因此在分子分母上都乘上一个常数C，不改变运算结果。
- 代码实现
```
     import numpy as np
     def softmax(a):
         c=np.max(a)
         exp_a=np.exp(a-c)  #避免溢出
         sum_exp_a=np.sum(exp_a)
         y=exp_a/sum_exp_a
         return y
```
- softmax函数输出是0.0到1.0之间的实数，并且输出总和为1。

权重初始化

全零初始化
- 这种方式并不适用，因为如果网络中的每个神经元都计算出同样的输出，然后它们就会在反向传播中计算出同样的梯度，从而进行同样的参数更新。换句话说，如果权重被初始化为同样的值，神经元之间就失去了不对称性的源头。
小随机数初始化
- 权重初始值要非常接近0又不能等于0。解决方法就是将权重初始化为很小的数值，以此来打
  破对称性。其思路是：如果神经元刚开始的时候是随机且不相等的，那么它们将计算出不同的更新，并将自身变成整个网络的不同部分。
- 小随机数权重初始化的实现方法是： W = 0.01 * np.random.randn(D,H) 。其中 randn 函数是基于零均值和标准差的一个高斯分布来生成随机数的。
- 但是并不是小数值一定会得到好的结果。例如，一个神经网络的层中的权重值很小，那么在反向传播的时候就会计算出非常小的梯度（因为梯度与权重值是成比例的）。这就会很大程度上减小反向传播中的“梯度信号”，在深度网络中，就会出现问题。
Xavier初始化
- 为了使各层的激活值呈现出具有相同广度的分布，推导了合适的权重尺度。如果前一层的节点数为n，则初始值使用标准差为 $\frac{1}{\sqrt{n}}$ 的分布。
- 代码实现

import numpy as np
node_num=100
w=np.random.randn(node_num,node_num)/np.sqrt(node_num)

Xavier初始值是以激活函数是线性函数为前提而推导出来的。因为sigmoid和tanh左右对称，且中央附近可以视作线性函数，所以适合使用Xavier初始值。但当激活函数是ReLU时，一般推荐使用He初始值。当前一层的节点数为n时，He初始值使用标准差为 $\sqrt\frac{2}{{n}}$ 的高斯分布，因为ReLU的负值区域的值为0，为了使它更有广度，所以需要2倍的系数。

损失函数

神经网络以某个指标为线索寻找最优权重参数，该指标成为损失函数。这个损失函数可以使用任意函数，但一般使用均方误差和交叉熵误差等

均方误差（mean squared error）
- $E=\frac{1}{2}(\sum(y_k-t_k)^2)$
- $y_k$ 表示神经网络的输出， $t_k$ 表示监督数据， $k$ 表示数据的维数
- 代码实现

import numpy as np
def mean_squared_error(y,t):
    return 0.5*np.sum((y-t)**2)

交叉熵误差（cross entropy error）
- $E=-\sum(t_klogy_k)$
- $t_k$ 中只有正确解标签的索引为1，其他均为0（one-hot表示）
- 所有训练数据的损失函数总和： $E=-\frac{1}{N}(\sum\limits_{n}\sum\limits_{k}t_{nk}logy_{nk})$
- 从全部数据中选出一部分，作为所有数据的近似，mini-batch(小批量)
- mini-batch版交叉熵误差代码实现（数据为标签形式）
```
   import numpy as np
   def cross_entropy_error(y,t):
       if y.ndim==1:    #y的维度为一，即求单个数据的交叉熵误差
           t=t.reshape(1,t.size)
           y=y.reshape(1,y.size)
       if t.size == y.size:
           t = t.argmax(axis=1)
       batch_size=y.shape[0]
       return -np.sum(np.log(y[np.arange(batch_size),t]+1e-7))
```

梯度下降

在梯度法中，函数的取值从当前位置沿着梯度方向前进一定距离，然后再新的地方重新求梯度，再沿着新梯度方向前进。像这样，通过不断地沿梯度方向前进，逐渐减小函数值地过程就是梯度法。寻找最小值地梯度法称为梯度下降法。

数值梯度

代码实现

def numerical_gradient(f, x):
    h = 1e-4 # 0.0001
    grad = np.zeros_like(x)  #生成和x形状相同地数组
    for idx in range(x.size):
        tmp_val=x[idx]
        x[idx]=tmp_val + h
        fxh1 = f(x) # f(x+h)

        x[idx] = tmp_val - h 
        fxh2 = f(x) # f(x-h)
        grad[idx] = (fxh1 - fxh2) / (2*h)

    return grad
   ```

梯度下降

代码实现

def gredient_descent(f, init_x,lr=0.01,step_num=100):
    x=init_x
    for i in range(step_num):
        grad=numerical_gradient(f,x)
        x -=lr*grad

   return x

像学习率这样的参数称为超参数。这是一种和神经网络的参数（权重和偏置）性质不同的参数（从数据中根据学习算法自动获得），学习率这样的超参数是人为设定的。

反向传播

正确理解误差反向传播法主要有两种，一是基于数学式，二是基于计算图。计算图将计算过程用图形表示出来以助于理解。

简单层的实现

层的实现中主要有两个共通的接口forward()和backward()。
乘法层和加法层的代码实现

 import numpy as np
  #乘法层的简单实现
 class Mullayer:  
     def __init__(self):
         self.x=None
         self.y=None
      
     def forward(self,x,y):
         self.x=x
         self.y=y
         out=x*y
         return out
  
     def backward(self,dout):
         dx=dout*self.y
         dy=dout*self.x
         return dx,dy
  
 #加法层
 class Addlayer:
  
     def __init__(self):
         self.x=None
         self.y=None
      
     def forward(self,x,y):
         self.x=x
         self.y=y
         out=x+y
         return out
  
     def backward(slef,dout):
         dx=dout*1
         dy=dout*1
         return dx,dy

激活函数层的实现

#Rectified Linear Unit
class ReLU:
   
    def __init__(self):
        self.mask=None
       
    def forward(self,x):
        self.mask=(x<=0)
        out=x.copy()
        out[self.mask]=0
        return out
   
    def backward(self,dout):
        dout[self.mask]=0
        dx=dout
        return dx
   
class sigmoid:
   
    def __init__(self):
        self.out=None
       
    def forward(self,x):
        out=1/(1+np.exp(-x))
        self.out=out
        return out
   
    def backward(self,dout):
        dx=dout*(1-self.out)*self.out
        return dx

Affine/Softmax层的实现

class Affine:
    def __init__(self,W,b):
        self.W=W
        self.b=b
        self.x=None
        self.dW=None
        self.db=None
       
    def forward(self,x):
        self.x=x
        out=np.dot(x,self.W)+self.b
        return out
   
    def backward(self,dout):
        dx=np.dot(dout,self.W.T)
        self.dW=np.dot(self.x.T,dout)
        self.db=np.sum(dout,axis=0)
       
        return dx

参数更新

神经网络的学习的目的时找到使损失函数的值尽可能小的参数，解决这个问题的过程称为最优化(optimization).使用参数的梯度，沿梯度方向更新参数，并重复这个步骤多次，从而逐渐靠近最优参数，这个过程称为随机梯度下降(stochastic gradient descent),即SGD。

SGD
- $W=W-η\frac{\partial{L}}{\partial{W}}$
- 这里把需要更新的权重参数记为 $W$ ,把损失函数关于 $W$ 的梯度记为 $\frac{\partial{L}}{\partial{W}}$ ,η表示学习率，实际上会取0.01或0.001这些事先决定好的值。
- 代码实现

import numpy as np
#stochastic gradient descent
class SGD:
    def __init__(self,lr=0.01):
        self.lr=lr       
    def update(self,params,grads):
        for key in params.keys():
            params[key]-=self.lr*grads[key]

SGD缺点：如果函数的形状非均向，比如呈延伸状，搜索的路径就会非常低效，其低效的根本原因是梯度的方向并没有指向最小值的方向
Momentum
- $v=αv-η\frac{\partial{L}}{\partial{W}}$
- $W = W + v$
- $α v$ 这一项表示物体再不受任何力时，承担使物体逐渐减速的任务，对应物理上的摩擦阻力。
- 代码实现

class Momentum:
    def __init__(self,lr=0.01,momentum=0.9):
        self.lr=lr
        self.momentum=momentum
        self.v=None
        
    def update(self,params,grads):
        if self.v is None:
            self.v={}
            for key,val in params.items():
                self.v[key]=np.zeros_like(val)
        
        for key in params.keys():
            self.v[key]=self.momentum*self.v[key]-self.lr*grads[key]
            params[key]+=self.v[key]

AdaGrad
- AdaGrad会为参数的每个元素适当地调整学习率，与此同时进行学习。
- $h=h+\frac{\partial{L}}{\partial{W}}·\frac{\partial{L}}{\partial{W}}$
- $W=W-η\frac{1}{\sqrt{h}}\frac{\partial{L}}{\partial{W}}$
- 新的变量h保存了以前所有梯度值地平方和。再更新参数时，通过乘以 $\frac{1}{\sqrt{h}}$ ,调整学习地尺度。这意味着，参数的元素中变动较大的元素学习率将变小。
- 代码实现

class AdaGrad:
    def __init__(self,lr=0.01):
        self.lr=lr
        self.h=None
       
    def update(self,params,grads):
        if self.h is None:
            self.h={}
            for key,val in params.items():
                self.h[key]=np.zeros_like(val)
               
        for key in params.keys():
            self.h[key]+=grads[key]*grads[key]
            params[key]-=self.lr*grads[key]/(np.sqrt(self.h[key])+1e-7)

正则化

$L_2$ 正则化比较常用，一般得到的权重会比较分散（diffuse）
$L_1$ 正则化，会引导稀疏化权重 sparse
可以把两个正则化都用上。如果不做特征选择时，不建议用 $L_1$
Max norm constraints 给一个上限，要求 $w∥_2<c$ ，注意这个和 RNN 的梯度裁剪不一样。这个是给权重加上界，那个是梯度。
Dropout 只有 p 的概率会激活，否则会置零。加在激活函数之前或者之后都是一样的。
Dropout的代码实现

import numpy as np

class Dropout:
    def __init__(self,dropout_ratio=0.5):
        self.dropout_ratio=dropout_ratio
        self.mask=None
    def forward(self,x,train_flg=True):
        if train_flg:
            self.mask=np.random.rand(*x.shape)>self.dropout_ratio
            return x*self.mask
        else:
            return x*(1.0-self.dropout_ratio)
     
    def backward(self,dout):
        return dout*self.mask