DP成魔之路

最新推荐文章于 2025-08-19 15:08:56 发布
最新推荐文章于 2025-08-19 15:08:56 发布
阅读量1k 收藏 15
点赞数 22
CC 4.0 BY-SA版权
文章标签： 笔记 算法
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/lxy___lxy/article/details/145257848

DP手的诞生

DP是这样的，出题人只要出题就好了，而做题的就要想很多了

喜欢和自己博弈，所以我要选DP

我有一道DP，你要不试试

又菜又爱，码垛

关注我，教我彻底学会DP

DP题集收纳

外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

背包——背不出来

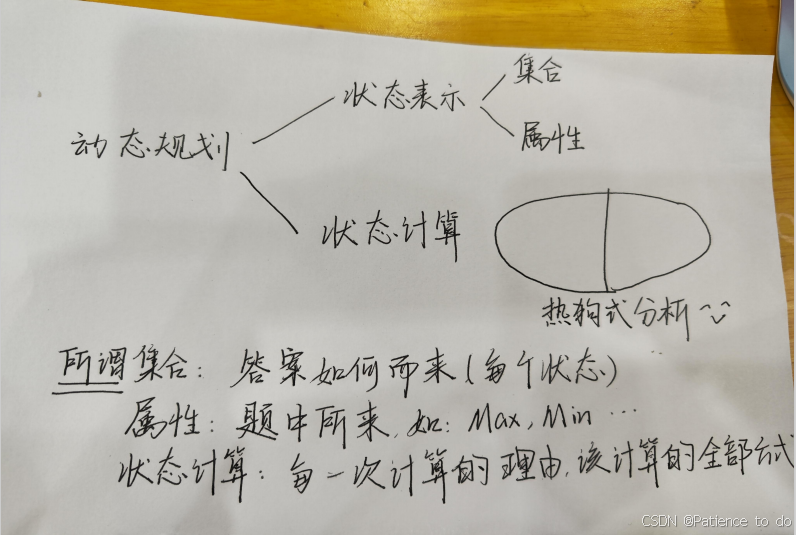
三状态背包

目标状态有三，你要怎么用，用谁，转换方程怎么写

**Problem：**n个食物，每个食物有a，b两个属性，你的胃两个属性的最大值分别是x，y，问最多能糟踏多少食物（咬一口也算糟蹋了）？

传送门：E - Maximum Glutton (atcoder.jp)

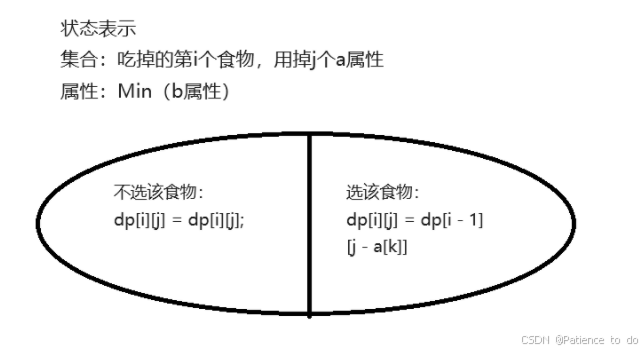
Ideas： （错误思路：正常来讲，我会直接把他当作一个普通的01背包，然后去贪心看看（分别用a,b属性对食物排序），果不其然wa了，后来就在想，用最小的替换掉大的，第i个物品作为二维数组变量1，a属性作为二维数组变量2，b属性作为二维数组的值1，个数作为值2，但是细想之后还是不对，因为用哪个来排序都行）（那就来说说正解：前文提到，二维数组有四个状态，但是b和个数谁来排序都不对，那么应该怎么做？前文是不是有个可有可无的变量呢？第几个物品，重要吗？好像，嗯…没用上啊那删掉，现在我总不能再拿b属性作为二维数组的变量1吧，那时间复杂度就超了，把个数当作变量1怎么样？然后只剩b数组作为值，斯，那这么说，如果个数能装到，并且使用a属性的时候让b属性尽可能小，那么，出现过的个数属性就是答案了！！！

理论形成，转换开始：

外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

Code：

#include <bits/stdc++.h>
#define int long long
#define endl "\n"

using namespace std;

const int N = 10010;

typedef long long LL;
typedef pair<int, int> PII;

int n;
int a[N], b[N];
int dp[100][N];
int x, y;

void solve() {
	cin >> n;
	cin >> x >> y;
	for(int i = 1; i <= n; i++) cin >> a[i] >> b[i];
	
	memset(dp, 0x3f, sizeof dp);
	dp[0][0] = 0;
	for(int i = 1; i <= n; i++) {
		for(int j = n; j; j--) {
			for(int k = a[i]; k <= x; k++) {
				if(dp[j - 1][k - a[i]] + b[i] <= y) dp[j][k] = min(dp[j][k], dp[j - 1][k - a[i]] + b[i]);
				
			}
		}
	}
	
	for(int i = n; i >= 0; i--) {
		for(int j = 0; j <= x; j++) {
			if(dp[i][j] <= 1e9) {
				cout << i + (i == n ? 0 : 1) << endl;
				return ;
			}
		}
	} 
}

signed main()
{
	ios::sync_with_stdio(false), cin.tie(0);
	cout.tie(0);
	
	int t = 1;
	// cin >> t;
	while(t--) {
		solve();
	}
}

10.16(1题）三角形的最大面积

Problem： 给定一个数组，问使用该数组构成的三角形的面积最大为多少

传送门：P1284 三角形牧场 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

Ideas： 存储两条边，然后通过总边长计算即可

#include <bits/stdc++.h>
#define int long long
#define endl "\n"

using namespace std;

const int N = 410;

typedef long long LL;
typedef pair<int, int> PII;

int n, sum;
int a[N];
int dp[N][N]; 

void solve() {
	cin >> n;
	for(int i = 1; i <= n; i++) cin >> a[i];
	dp[0][0] = 1;
	for(int i = 1; i <= n; i++) {
		sum += a[i];
		for(int j = 400; j >= 0; j--) {
			for(int k = 400; k >= 0; k--) {
				if(j >= a[i] && dp[j - a[i]][k] == 1) dp[j][k] = 1;
				if(k >= a[i] && dp[j][k - a[i]] == 1) dp[j][k] = 1;
			}
		}
	}
	int res = 0;
	int q = sum / 2;
	for(int j = 1; j <= 400; j++) {
		for(int k = 1; k <= 400; k++) {
			if(!dp[j][k]) continue;
			res = max(res, (int)(100 * sqrt(q * (q - j) * (q - k) * (q - (sum - j - k)))));
		}
	}
	cout << res << endl;
}

signed main()
{
	ios::sync_with_stdio(false), cin.tie(0);
	cout.tie(0);
	
	int t = 1;
//	cin >> t;
	while(t--) {
		solve();
	}
}

10.16（2题）奶牛智商和情商都不可为负数的和最大值

Problem： n头奶牛，s,f两个值代表智商和情商，问和皆为正数的和的最大值是多少

传送门： [P2340 USACO03FALL] Cow Exhibition G - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

Ideas： 存储一个智商，然后考虑到会存在负数的情况下标会越界，先给智商从大到小排序，然后进行背包即可

#include <bits/stdc++.h>
#define int long long
#define endl "\n"

using namespace std;

const int N = 4e6 + 10;

typedef long long LL;
typedef pair<int, int> PII;

int n;
struct P {
	int a, b;
} a[N];
int dp[N];

void solve() {
	cin >> n;
	for(int i = 1; i <= n; i++) cin >> a[i].a >> a[i].b;
	sort(a + 1, a + 1 + n, [&](const P &a, const P &b) {
		return a.a > b.a;
	});
	memset(dp, -0x3f, sizeof dp);
	
	dp[0] = 0;
	int ma = 0;
	for(int i = 1; i <= n; i++) {
		ma += abs(a[i].a);
		if(a[i].a >= 0)
			for(int j = ma; j >= 0; j--) {
				if(j >= a[i].a && j + a[i].a >= 0 && dp[j - a[i].a] >= -4000000) {
					dp[j] = max(dp[j], dp[j - a[i].a] + a[i].b);
				}
			}
		else {
			for(int j = 0; j <= ma; j++) {
				if(j >= a[i].a && j - a[i].a <= ma && dp[j - a[i].a] >= -4000000) {
					dp[j] = max(dp[j], dp[j - a[i].a] + a[i].b);
				}
			}
		}
	} 
	int res = 0;
	for(int i = 0; i < ma; i++) {
		if(dp[i] >= 0) res = max(res, i + dp[i]);
	}
	cout << res << endl;
}

signed main()
{
	ios::sync_with_stdio(false), cin.tie(0);
	cout.tie(0);
	
	int t = 1;
	// cin >> t;
	while(t--) {
		solve();
	}
}

10.16（3题） 背包之取物后问情况数量

Problem： n个物品，每个物品有自己的重量，你有一个背包的容量是m，问你分别把每个物品都去除后背包刚好被装满的方式有多少种？输出分别取出n个物品后该背包容量从1~m的末位。

传送门： P4141 消失之物 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

Ideas： 首先把所有的物品都用上，然后分别对每个物品处理，他的转换就是通过消除这个物品的影响然后传递下去。

错误原因：数据溢出

#include <bits/stdc++.h>
#define int long long
#define endl "\n"

using namespace std;

const int N = 4010;

typedef long long LL;
typedef pair<int, int> PII;

int n, m;
int a[N];
int dp[N];

void solve() {
	cin >> n >> m;
	for(int i = 1; i <= n; i++) cin >> a[i];
	
	dp[0] = 1;
	for(int i = 1; i <= n; i++) {
		for(int j = N - 5; j >= 0; j--) {
			if(j >= a[i]) dp[j] += dp[j - a[i]];
			dp[j] %= 10;
		}
	}

	for(int i = 1; i <= n; i++) {
		int dp2[N];
		memcpy(dp2, dp, sizeof dp2);
		for(int j = 1; j <= m; j++) {
			if(j - a[i] >= 0 && dp2[j - a[i]]) dp2[j] -= dp2[j - a[i]];
			cout << (dp2[j] % 10 + 10) % 10;
		}
		cout << endl;
	}
}

signed main()
{
	ios::sync_with_stdio(false), cin.tie(0);
	cout.tie(0);
	
	int t = 1;
	// cin >> t;
	while(t--) {
		solve();
	}
}

10.18-10.20（3题）两状态背包，但只能存一个状态，另一个状态用优先队列处理

Problem： 有n个物品，你有m块钱，你有k次免费获得物品的机会，每个物品有两个属性，一个是价格，一个是满意度，你想要获得更多的满意度

传送门： Problem - G - Codeforces

Ideas： 先按照价格排序用01背包解决钱的问题，然后用优先队列存储k个物品价值大的

#include <bits/stdc++.h>
#define int long long
#define endl "\n"

using namespace std;

const int N = 5e3 + 10, M = 1e4 + 10;

typedef long long LL;
typedef pair<int, int> PII;

int n, m, s;
struct {
	int w, v;
} a[N];
int dp[M];

void solve() {
	cin >> n >> m >> s;
	for(int i = 1; i <= n; i++) cin >> a[i].w >> a[i].v;
	
	sort(a + 1, a + 1 + n, [&](const auto &A, const auto &B) {
		return A.w < B.w;
	});
	
	
	int res = 0;
	for(int i = 1; i <= n; i++) {
		int ans = 0;
		for(int j = m; j >= 0; j--) {
			if(j >= a[i].w) dp[j] = max(dp[j], dp[j - a[i].w] + a[i].v);
			ans = max(ans, dp[j]);
		}
		priority_queue<int> q;
		while(q.size()) q.pop();
		for(int j = i + 1; j <= n; j++) {
			q.push(a[j].v);
		}
		int k = s;
		while(k-- && q.size()) {
			ans += q.top(); q.pop();
		}
		res = max(res, ans);
		// cout << ans << endl;
	}
	cout << res << endl;
}

signed main()
{
	ios::sync_with_stdio(false), cin.tie(0);
	cout.tie(0);
	int t = 1;
	// cin >> t;
	while(t--) {
		solve();
	}
}

序列和矩阵DP优化

三状态转移

Problem: 给定一个矩阵，要求每一行都选择一个区间，并在相邻行的区间有交，最大化选中的数字和

碎碎念：赛时的时候想到了状态转移的方法，但是没有想清楚状态转移的方程，还是太菜了

传送门： I-Intersecting Intervals_2024牛客暑期多校训练营6 (nowcoder.com)

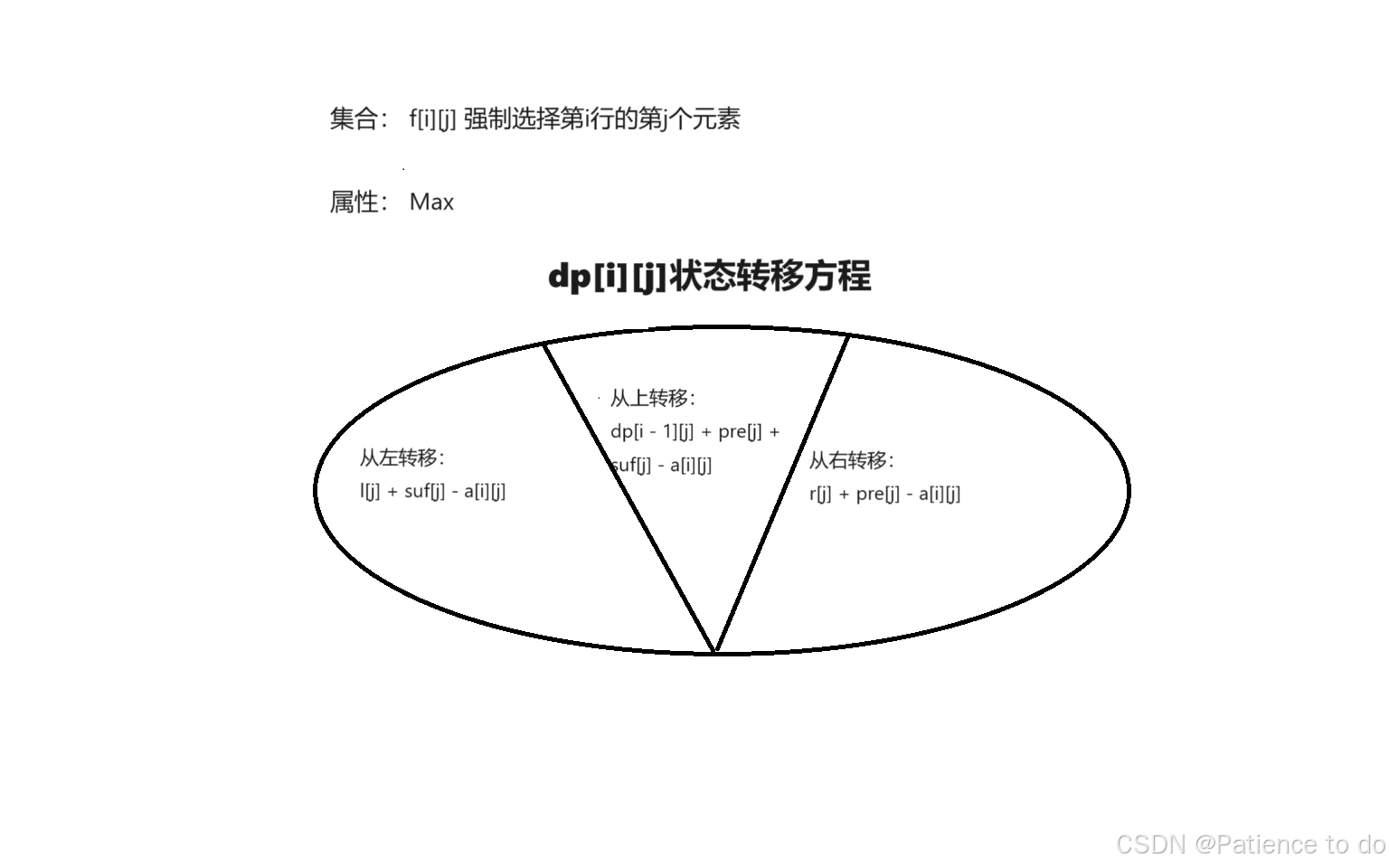
Ideas： 对于dp[i][j] 的定义为第i行强制选择第j个作为最大化的值，那么，不难发现，它可以从三个方向进行状态转移。上面，左边，右边。另外需要两个数组，pre表示该行以j作为结尾的最大子序列pre[j] = max(pre[j - 1] + a[i][j], a[i][j])，suf表示以改行以j作为开始的最大子序列 suf[j] = max(suf[j + 1] + a[i][j], a[i][j]) ，那么，从上面的转移就很清楚了，dp[i][j] = d[i - 1][j] + pre[j] + suf[j] - a[i][j] ，那么，左边的转移又怎么处理？用一个l数组表示该行以j结尾的最大子序列，去存储不考虑该行j~m的值，因为suf[j] 里面存储了右边的最大连续子序列，那么l[j] = max(l[j - 1] + a[i][j], dp[i - 1][j] + pre[j]); 对于dp[i][j] 来说的转移就是 dp[i][j] = max(dp[i][j], l[j] + suf[j] - a[i][j]); 右边同理。

外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

Code：

void solve() {
	int n, m;
	cin >> n >> m;
	vector<vector<int>> a(n + 2, vector<int> (m + 2));
	vector<vector<int>> dp(n + 2, vector<int> (m + 2));
	
	for(int i = 1; i <= n; i++) {
		vector<int> pre(m + 2), suf(m + 2);
		vector<int> l(m + 2), r(m + 2);
		pre[0] = 0, suf[m + 1] = 0;
		for(int j = 1; j <= m; j++) {
			cin >> a[i][j];
		}
		for(int j = 1; j <= m; j++) {
			pre[j] = max(pre[j - 1] + a[i][j], a[i][j]);
		}
		for(int j = m; j >= 1; j--) {
			suf[j] = max(suf[j + 1] + a[i][j], a[i][j]);
		}
		l[0] = -1e18, r[m + 1] = -1e18;
		for(int j = 1; j <= m; j++) {
			l[j] = max(l[j - 1] + a[i][j], dp[i - 1][j] + pre[j]);
			dp[i][j] = l[j] + suf[j] - a[i][j];
		}
		for(int j = m; j >= 1; j--) {
			r[j] = max(r[j + 1] + a[i][j], dp[i - 1][j] + suf[j]);
			dp[i][j] = max(dp[i][j], r[j] + pre[j] - a[i][j]);
		}
	}
	
	int res = -1e18;
	for(int i = 1; i <= m; i++) {
		res = max(res, dp[n][i]);
	}
	cout << res << endl;
}

子序列转换问题

序列乘积个位数为6个数问题

**Problem：**对于一个数组，求有多少个子序列的fi中个位数是6的数字个数

传送门：E-小红的序列乘积2.0_牛客周赛 Round 55 (nowcoder.com)

Ideas： 把每一个状态记录下来，记录到第i个数中从1~9的个位数的个数记录后，通过每一次乘上a[i]获得新的状态转换，如果产生了乘积的求余为6，那么就一定会对后面的每一种情况都产生一种排列计数，那么通过快速幂进行乘法计算即可，转换过程通过for循环去依次遍历1到9，然后每一个都乘以a[i]即可

#include <bits/stdc++.h>
#define int long long
#define endl "\n"

using namespace std;

const int N = 2e5 + 10, mod = 1e9 + 7;

typedef pair<int, int> PII;
typedef long long LL;

int n;
int a[N];
int dp[15][2];

int qmi(int a, int k) {
	int res = 1;
	while(k) {
		if(k & 1) res = res * a % mod;
		k >>= 1;
		a = a * a % mod;
	}
	return res;
}

void solve() {
	cin >> n;
	for(int i = 1; i <= n; i++) cin >> a[i];
	
	int res = 0;
	dp[1][0] = 1;
	int last = 1, now = 0;
	for(int i = 1; i <= n; i++) {
		swap(last, now);
		for(int j = 0; j <= 9; j++) dp[j][now] = dp[j][last];
		
		for(int j = 0; j <= 9; j++) {
			dp[j * a[i] % 10][now] += dp[j][last];
			dp[j * a[i] % 10][now] %= mod;
			if(j * a[i] % 10 == 6) res += dp[j][last] * qmi(2, n - i), res %= mod;
		}
		
		// for(int j = 0; j <= 9; j++) cout << dp[j][now] << ' ';
		// cout << endl;
	}
	cout << res << endl;
}

signed main()
{
	ios::sync_with_stdio(false), cin.tie(0);
	cout.tie(0);
	
	int t = 1;
	// cin >> t;
	while(t--) {
		solve();
	}
}

10.14（1题） 子序列的a[i]&a[i - 1]!=0

Problem： 给定一个数组，求k的最大值，满足a[i]&a[i - 1]!=0（2<=i<=k)

传送门：P4310 绝世好题 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

Ideas： 按位拆分，后对每一位进行分割

#include <bits/stdc++.h>
#define int long long
#define endl "\n"

using namespace std;

const int N = 1e5 + 10;

typedef long long LL;
typedef pair<int, int> PII;

int n;
int a[N];
int dp[50];

void solve() {
	cin >> n;
	for(int i = 1; i <= n; i++) cin >> a[i];
	memset(dp, 0, sizeof dp);
	int x = a[1];
	int j = 0;
	while(x) {
		dp[++j] = x % 2;
		x /= 2;
	}
	
	int res = 0;
	int now = 0, last = 1;
	for(int i = 2; i <= n; i++) {
		int x = a[i];
		int dp2[50];
		memcpy(dp2, dp, sizeof dp2);
		vector<int> st; st.clear();
		
		for(int j = 1; x; j++) {
			if(x & 1) st.push_back(j);
			x /= 2;
		}
		for(auto A : st) {
			for(auto B : st) {
				dp[B] = max(dp[B], dp2[A] + 1);
			}
		}
	}
	for(int i = 1; i < 49; i++) res = max(res, dp[i]);
	cout << res << endl;
	
}

signed main()
{
	ios::sync_with_stdio(false), cin.tie(0);
	cout.tie(0);
	
	int t = 1;
//	cin >> t;
	while(t--) {
		solve();
	}
}

子串问题

10.14（2题）子串的匹配问题

Problem： (),[]匹配子串，问最长能够匹配的子串是哪个子串？

传送门： P1944 最长括号匹配 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

Ideas： dp存储的是以当前位置结尾能够匹配的最大子串长度，转移来自于本身加上前面可以连贯的长度

{总结：这个题目没想到，看到题解提示了一句以当前位置结尾才顿悟了，这个思维得有}

#include <bits/stdc++.h>
#define int long long
#define endl "\n"

using namespace std;

const int N = 1e6 + 10;

typedef long long LL;
typedef pair<int, int> PII;

string s;
int dp[N];

void solve() {
	cin >> s;
	int n = s.size();
	s = " " + s;
	int res = 0;
	for(int i = 1; i <= n; i++) {
		if(s[i] == '(' || s[i] == '[') dp[i] = 0;
		else if(s[i] == ')') {
			if(s[i - dp[i - 1] * 2 - 1] == '(') {
				dp[i] = dp[i - 1] + 1 + dp[i - 2 - 2 * dp[i - 1]];
			}
			else {
				dp[i] = 0;
			}
		}
		else {
			if(s[i - dp[i - 1] * 2 - 1] == '[') {
				dp[i] = dp[i - 1] + 1 + dp[i - 2 - 2 * dp[i - 1]];
			}
			else {
				dp[i] = 0;
			}
		}
	}
	int mx = 1;
	for(int i = 1; i <= n; i++) {
		if(dp[mx] < dp[i]) mx = i;
//		cout << dp[i] << " ";
	}
//	cout << endl;
	for(int i = mx - 2 * dp[mx] + 1; i <= mx; i++) cout << s[i];
	cout << endl;
}

signed main()
{
	ios::sync_with_stdio(false), cin.tie(0);
	cout.tie(0);
	
	int t = 1;
//	cin >> t;
	while(t--) {
		solve();
	}
}

树形&换根

10.17（1题）最大子树和（换根）

Problem： 找到子树和的最大值，要求至少保留一根树枝，其次树枝必须通过边连着

传送门： P1122 最大子树和 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

Ideas： 直接树形dp跑一边，然后另外用一个数组换根dp求一边答案就在后一个数组中，取Max即可，但要注意不能忘记必须要至少保留一根树枝

#include <bits/stdc++.h>
#define int long long
#define endl "\n"

using namespace std;

const int N = 16010;

typedef long long LL;
typedef pair<int, int> PII;

int n;
int a[N];
int dp[N], dp2[N];
vector<int> h[N];
int res = -1e18;

void dfs(int u, int fa) {
	dp[u] = a[u];
	for(auto A : h[u]) {
		if(A == fa) continue;
		
		dfs(A, u);
		if(dp[A] >= 0) dp[u] += dp[A];
	}
}

void dfs2(int u, int fa) {
	dp2[u] = a[u];
	for(auto A : h[u]) {
		if(A == fa) continue;
		
		dfs2(A, u);
		if(dp[A] >= 0) dp2[u] += dp[A];
	}
	res = max(res, dp2[u]);
}

void solve() {
	cin >> n;
	for(int i = 1; i <= n; i++) cin >> a[i];
	for(int i = 1; i < n; i++) {
		int x, y;
		cin >> x >> y;
		h[x].push_back(y);
		h[y].push_back(x);
	}
	
	dfs(1, 0);
	dfs2(1, 0);

	cout << res << endl;
}

signed main()
{
	ios::sync_with_stdio(false), cin.tie(0);
	cout.tie(0);
	
	int t = 1;
	// cin >> t;
	while(t--) {
		solve();
	}
}

10.17（2题）没有上司的舞会

Problem： 上司参加舞会，下属就不会参加，每个人都有一个快乐指数，问邀请那些职员的最大快乐指数是多少？

传送门： P1352 没有上司的舞会 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

Ideas： 直接树形dp，每个点存储两个信息，一个自己不去，一个自己去，答案在树顶的两个值中的Max

#include <bits/stdc++.h>
#define int long long
#define endl "\n"

using namespace std;

const int N = 6e3 + 10;

typedef long long LL;
typedef pair<int, int> PII;

int n;
int a[N];
int dp[N][2];
vector<int> h[N];

void dfs(int u, int fa) {
	dp[u][0] = a[u];
	
	for(auto A : h[u]) {
		if(A == fa) continue;
		dfs(A, u);
		dp[u][0] += dp[A][1];
		dp[u][1] += max(dp[A][0], dp[A][1]);
	}
}

void solve() {
	cin >> n;
	for(int i = 1; i <= n; i++) cin >> a[i];
	for(int i = 1; i < n; i++) {
		int x, y;
		cin >> x >> y;
		h[x].push_back(y);
		h[y].push_back(x);
	}
	
	dfs(1, 0);
	cout << max(dp[1][0], dp[1][1]) << endl;
}

signed main()
{
	ios::sync_with_stdio(false), cin.tie(0);
	cout.tie(0);
	
	int t = 1;
	// cin >> t;
	while(t--) {
		solve();
	}
}

10.17（3题）一条边至少有一个点被选中

Problem： 一个无根树，n个节点和n-1条边，问最少选中多少个节点可以让所有的边的两端至少有一段被选中。

传送门： P2016 战略游戏 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

Ideas： 两个状态，分别存储该节点被选和不被选，但要注意他的起始位置是从0开始的

#include <bits/stdc++.h>
#define int long long
#define endl "\n"

using namespace std;

const int N = 1510;

typedef long long LL;
typedef pair<int, int> PII;

int n;
vector<int> h[N];
int dp[N][2];

void dfs(int u, int fa) {
	dp[u][0] = 1;
	
	for(auto A : h[u]) {
		if(A == fa) continue;
		
		dfs(A, u);
		dp[u][0] += min(dp[A][0], dp[A][1]);
		dp[u][1] += dp[A][0];
	}
}

void solve() {
	cin >> n;
	for(int i = 1; i <= n; i++) {
		int x, q;
		cin >> x >> q;
		for(int j = 1; j <= q; j++) {
			int y;
			cin >> y;
			h[x].push_back(y);
			h[y].push_back(x);
		}
	}
	
	dfs(0, -1);
	cout << min(dp[0][0], dp[0][1]) << endl;
}

signed main()
{
	ios::sync_with_stdio(false), cin.tie(0);
	cout.tie(0);
	
	int t = 1;
	// cin >> t;
	while(t--) {
		solve();
	}
}

其他DP

10.18-10.20（1题）通过矩阵的方块求最大值

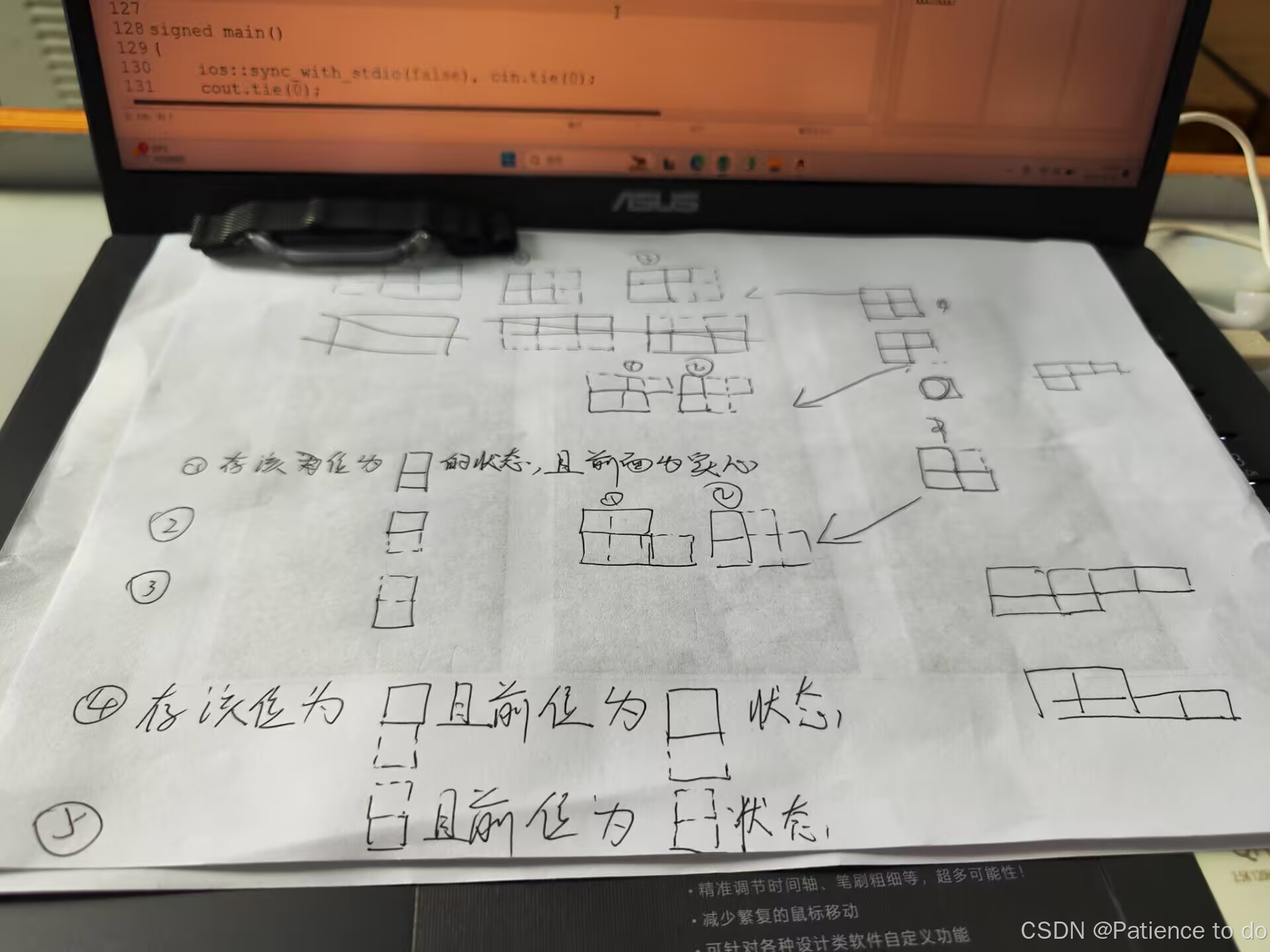
Problem： 给定一个2*n的矩阵，每个方块有A或J两个值，需要划分连续的三个格子，如果格子有>=2个A，则总数+1，问总数最大是多少？

传送门：Problem - C - Codeforces

Ideas： 本题的转换比较麻烦，我开了五个dp数组，存储不同的状态，具体见下图

外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

#include <bits/stdc++.h>
#define int long long
#define endl "\n"

using namespace std;

const int N = 1e5 + 10;

typedef long long LL;
typedef pair<int, int> PII;

int n;
string a, b;
int dp1[N]; // 两
int dp2[N]; // 上
int dp3[N]; // 下
int dp4[N]; // 两个连续的上
int dp5[N]; // 两个连续的下

void solve() {
	a = b = "";
	cin >> n >> a >> b;
	a = " " + a, b = " " + b; 
	for(int i = 0; i <= n; i++) dp1[i] = dp2[i] = dp3[i] = dp4[i] = dp5[i] = 0;
	
	for(int i = 1; i <= n; i++) {
		//dp1 
		// ①
		if(i >= 3) {
			int q = 0, q2 = 0, sum = 0;
			for(int j = i - 2; j <= i; j++) {
				if(a[j] == 'A') q++;
				if(b[j] == 'A') q2++;
			}
			if(q >= 2) sum++;
			if(q2>= 2) sum++;
			dp1[i] = max(dp1[i], dp1[i - 3] + sum);
		}
		// ②
		if(i >= 3) {
			int q = 0, sum = 0;
			if(a[i - 1] == 'A') q++; 
			if(a[i] == 'A') q++;
			if(b[i] == 'A') q++;
			if(q >= 2) sum++;
			dp1[i] = max(dp1[i], dp3[i - 1] + sum);
		}
		// ③
		if(i >= 3) {
			int q = 0, sum = 0;
			if(b[i - 1] == 'A') q++; 
			if(a[i] == 'A') q++;
			if(b[i] == 'A') q++;
			if(q >= 2) sum++;
			dp1[i] = max(dp1[i], dp2[i - 1] + sum);
		}
		
		// dp2
		// ①
		if(i >= 3) {
			int q = 0, sum = 0;
			for(int j = i - 2; j <= i; j++) {
				if(a[j] == 'A') q++;
			}
			if(q >= 2) sum++;
			dp2[i] = max(dp2[i], dp5[i - 1] + sum);
		}
		
		// ②
		if(i >= 2) {
			int q = 0, sum = 0;
			if(a[i - 1] == 'A') q++; 
			if(a[i] == 'A') q++;
			if(b[i - 1] == 'A') q++;
			if(q >= 2) sum++;
			// cout << i << ' ' << q << endl;
			dp2[i] = max(dp2[i], dp1[i - 2] + sum);
		}
		
		// dp3
		// ①
		if(i >= 3) {
			int q = 0, sum = 0;
			for(int j = i - 2; j <= i; j++) {
				if(b[j] == 'A') q++;
			}
			if(q >= 2) sum++;
			dp3[i] = max(dp3[i], dp4[i - 1] + sum);
		}
		
		// ②
		if(i >= 2) {
			int q = 0, sum = 0;
			if(b[i - 1] == 'A') q++; 
			if(a[i - 1] == 'A') q++;
			if(b[i] == 'A') q++;
			if(q >= 2) sum++;
			dp3[i] = max(dp3[i], dp1[i - 2] + sum);
		}
		
		// dp4
		if(i >= 4) {
			int q = 0, sum = 0;
			for(int j = i - 2; j <= i; j++) {
				if(a[j] == 'A') q++;
			}
			if(q >= 2) sum++;
			dp4[i] = max(dp4[i], dp3[i - 2] + sum);
		}
		// dp5
		if(i >= 4) {
			int q = 0, sum = 0;
			for(int j = i - 2; j <= i; j++) {
				if(b[j] == 'A') q++;
			}
			if(q >= 2) sum++;
			dp5[i] = max(dp5[i], dp2[i - 2] + sum);
		}
	}	
	cout << dp1[n] << endl;
}

signed main()
{
	ios::sync_with_stdio(false), cin.tie(0);
	cout.tie(0);
	
	int t = 1;
	cin >> t;
	while(t--) {
		solve();
	}
}

10.18-10.20（2题）一个属性可以添加到两个属性的情况

Problem： 你有一些自由属性点，给你一个数组，如果是0则表示你获得了一个自由属性点，如果是>0的数，则表示力量，如果你的力量值达到则总数+1，<0的数表示智商，如果智商达到则总数+1，问你的总数最大能达到多少

传送门： Problem - D - Codeforces

Ideas： 开一个dp数组，对于每个0都进行转换，时间复杂度为m*m（m<5000)，存储的信息为：当前位置力量为i的情况下获得的最大收益

#include <bits/stdc++.h>
#define int long long
#define endl "\n"

using namespace std;

const int N = 5010, M = 2e6 + 10;

typedef long long LL;
typedef pair<int, int> PII;

int n, m;
int a[M];
int dp[N]; // 当前位置下的正数个数的最大值
int b[N], c[N]; // 正数， 负数

void solve() {
	cin >> n >> m;
	for(int i = 1; i <= n; i++) cin >> a[i];
	a[++n] = 0;
	int sum = 0;
	for(int i = 1; i <= n; i++) {
		if(a[i] == 0) {
			for(int j = 1; j <= sum; j++) b[j] += b[j - 1];
			for(int j = 1; j <= sum; j++) c[j] += c[j - 1];

			for(int j = sum; j >= 0; j--) {
				if(j >= 1) dp[j] = max(dp[j] + c[sum - j] + b[j], dp[j - 1] + b[j] + c[sum - j]);
				else dp[j] = dp[j] + c[sum - j];
			}
			
			sum++;
			for(int j = 0; j <= m + 5; j++) b[j] = c[j] = 0;
		}
		else {
			if(a[i] > 0 && a[i] <= sum) b[a[i]]++;
			if(a[i] < 0 && abs(a[i]) <= sum) c[abs(a[i])]++;
		}
	}
	
	int res = 0;
	for(int i = 0; i <= m; i++) {
		res = max(res, dp[i]);
	}
	cout << res << endl;
}

signed main()
{
	ios::sync_with_stdio(false), cin.tie(0);
	cout.tie(0);
	
	int t = 1;
	// cin >> t;
	while(t--) {
		solve();
	}
}

10.22（1题）拼接串，位运算DP

Problem： 给定一个长度为n的正整数串a,先可以把两个没有重叠的连续子串前后拼接起来，但要求拼接之后的数串中每个正整数都不能出现超过一次，问最大长度。

Ideas： 这个题目很容易陷入思维惯例，就会设置一个dp数组，存储当前位置的最大长度的拼接，但是不行，正确的做法应该是通过题目给定的18位，然后开辟数组dp长度为2^18，将其每一位的放置变成考虑到每一个数字的放法，然后通过每一个位从后循环18位，就能够获取该dp数组，然后通过一种方式去得到两个拼接串。

外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

#include <bits/stdc++.h>
#define int long long
#define endl "\n"

using namespace std;

const int N = 1e6 + 10;

int n;
int a[N];
int dp[N];

void solve() {
	cin >> n;
	for(int i = 1; i <= n; i++) cin >> a[i];
	
	for(int i = 1; i <= n; i++) {
		bool st[20];
		int s = 0;
		memset(st, false, sizeof st);
		for(int j = i; j <= i + 18; j++) {
			if(st[a[j]] || j > n) break;
			st[a[j]] = true;
			s += 1 << (a[j] - 1);
			dp[s] = max(dp[s], j - i + 1);
		}
	}
	
	int res = 0;
	int q = 1 << 18;
	for(int i = 1; i <= q; i++) {
		for(int j = i; j > 0; j = i&j-1) {
			res = max(res, dp[j] + dp[i ^ j]);
		}
		
	}
	cout << res << endl;
}

signed main()
{
	ios::sync_with_stdio(false), cin.tie(0);
	cout.tie(0);
	
	
	solve();
}

10.23（1题）单调队列维护dp

Problem： 输入一个长度n的序列，找出一段长度不超过m的连续子序列，使得子序列中所有数的和最大。

Ideas： 通过维护一个单调上升的队列，存放的是位置下标，维护的是原序列的前缀和。

#include <cstring>
#include <iostream>
#include <algorithm>
#include <limits.h>

using namespace std;

const int N = 300010;

int n, m;
int s[N];
int q[N];

int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i ++ ) scanf("%d", &s[i]), s[i] += s[i - 1];

    int res = 1e-18;
    int hh = 0, tt = 0;

    for (int i = 1; i <= n; i ++ )
    {
        if (q[hh] < i - m) hh ++ ;
        res = max(res, s[i] - s[q[hh]]);
        while (hh <= tt && s[q[tt]] >= s[i]) tt -- ;
        q[ ++ tt] = i;
    }

    printf("%d\n", res);

    return 0;
}

12.23（2题）数塔

Problem： 免费馅饼，你站在数轴为五的位置，每一秒可以移动一格或者原地不动，现在有n组馅饼，属性分别是a代表下落在数轴的位置，b代表下落的秒数，你不能让馅饼落地，问最多能够接多少个饼？

Ideas： 数塔

【A2DP】深入解析A2DP协议中的音频流处理
[byte轻骑兵] 的技术小窝！
03-12 4827
A2DP 应用层通过严谨的音频流设置流程和高效的音频流传输过程，实现了高质量音频在蓝牙设备间的稳定传输。深入理解这些流程和要求，能够更好地优化设备性能，提升用户体验，确保设备在复杂的蓝牙音频环境中稳定运行，满足不断增长的音频应用需求。
蓝魔法师（树形DP）
Ray.C.L的博客
08-05 320
思路：树上求方案，dp[i][j]表示以i的子树里连通块个数为j的方案数（j<=k）这里我们有2个选择， 1.删除当前边,此时节点u与他的的子节点v所能构成的方案数就是dp[u][x]乘上dp[v][1——x] dp[u][x]=dp[u][x]∗∑i=1xdp[v][i]dp[u][x]= dp[u][x]*\sum_{i=1}^xdp[v][i]dp[u][x]=dp[u][x]∗∑i=1x​dp[v][i] 2.不删除当前边,此时节点u与节点v构成i+j（i为u的连通块个数,j为v的连通块个数.
DP成魔之路——梦开始的地方
lxy___lxy的博客
07-29 373
我有很多道DP，你要不试试
小小的dp魔法
apricot0402的博客
03-12 683
至此，我们解答了问题1和问题2的不同，那么内外循环的换序为什么可以从统计集合变为统计序列呢（当两个set互相拥有对方所有拥有的元素则相同，当array中对应元素相同才相同）我们继续使用上一个例子。而在外循环逆序遍历和数，那么目标数N一开始状态就被锁死在0了，因为我们假设dp[i - j]已经被计算好了，但逆序遍历的话当前dp[i - j]还没遍历到呢？如果我们先遍历零数集合的可能性（1，2），也就是把M放外圈，那么我们现在先把1取出来，让内圈数字（1~5）用这个数字来构成自己。外循环不再有，内循环常停留。
树形 DP：编程世界的神奇魔法树之旅
你猜我是谁？
11-16 1517
哇哦！树形 DP 那可绝对是编程算法世界里一颗亮瞎眼的魔法之星啊！它就像宇宙中心那团最耀眼的火焰，光芒万丈，神奇得一塌糊涂。它的厉害之处可不只是能把树形结构相关的问题轻松搞定这么简单，那简直就是小菜一碟儿，它真正牛气哄哄的地方在于藏在其中那独特得像来自外星球的思维方式和算法设计理念。你瞧，它就像一位从远古魔法时代穿越而来的魔法导师，那身上的神秘气息都能把周围的空气变得闪闪发光。
YBTOJ：魔法数字（数位dp）
BUG_Creater_jie的博客
07-21 446
文章目录题目描述解析 题目描述 解析 迷惑。。。 首先，比较容易想到用二进制状态压缩记录1-9是否在十进制中出现过 然后就是整除的问题 如果记录余数，它的模数又有9个 开九维余数直接爆炸。。。 怎么办嘞？ 有一个结论： 若ｋ为p1、p2…pn的公倍数 那么(x%k)%pi=x%pi 因为k是p的质数，所以这个结论还是挺显然的 那么本题就可以找到1-9的最小公倍数（为2520） 使它作为模数最后再进行判断即可 时间复杂度：18（位数）*512（状态压缩）*2520（取模结果）*10（每次dp枚举）=23
hdu 4545 魔法串 dp
zyh
04-21 558
题目链接： http://acm.hdu.edu.cn/showproblem.php?pid=4545 思路：设dp[i][j]为s1长度为i，s2长度为j能否成功匹配，状态出来后，详细的转移方程看代码 #include #include #include using namespace std; char s1[1005], s2[1005]; int m
H 施魔法 区间dp
qq_44335608的博客
02-09 186
H 施魔法 题意：给你n个物品，每个物品有各自的权值，你每次至少选择k个物品作为一组，选择后这一组就会产生max(ai…ak) - min(ai…ak) 的贡献，要求你将n件物品分为x组后，总贡献最小。 题解：首先肯定排序，这没有什么好解释的。 设dp[i]代表i件物品的最小花费。 那么dp[i] = min{ dp[j] + a[i] - a[j+1] } ( 1<= j <= i-...
冰封魔法 DP
Bell的博客
10-31 452
冰封魔法 终于，feluamn 通过了蛮人族族长的考核。又是数个月穿梭于黑暗中，feluamn 终于站在了光明之巅前。 而黑暗之心蒙蔽了光明，通往光明之巅的路已经化为泥泞。 feluamn 这么干净漂亮的女孩子当然是不愿意跨入泥泞的。 但是 feluamn 也 有她的办法。feluamn 动用了她的冰系魔法…… feluamn 面前是一条长度为 n 的泥泞道路。 feluamn 可以花费 x 点魔力释放冰系魔法来冻住 x − 1 到 x （x 为整数）的位置。 同时，在某些位置，由于能触动自然界中的冰元素，
vijos 1417 魔法塔防 - DP
Mys_C_K的博客
08-03 465
传送门 题解：显然红塔放在最后。 dp[i][j]表示前i座塔放了几个绿塔，剩下的放红塔。 这样是O(n^2)的。 此题显然可以做到O(gb+n)的复杂度。 可以通过形如n 发现可以优化空间。 //vijos 1411 #include #include #include #include #define lint long long #define N 1100 using nam
哈理工2249开锁魔法 概率dp
u013268685的专栏(有一种幸福叫AC，有一种期待叫AK)
04-11 932
开锁魔法II Time Limit: 3000 MS Memory Limit: 256000 K Total Submit: 23(18 users) Total Accepted: 18(16 users) Rating:  Special Judge: No Description 一日，
PolygonGame:DP 多边形游戏可视化
05-18
在编程领域，尤其是算法设计中，动态规划（Dynamic Programming, DP）是一种极其重要的解决复杂问题的方法。它通过将问题分解为子问题，并存储子问题的解以避免重复计算，从而达到优化求解效率的目的。本文将探讨一...
2020牛客寒假算法基础集训营2——H.施魔法【DP】
NIRVANA REBIRTH
02-06 756
题目传送门 题目描述 牛可乐有 n 个元素( 编号 1…n )，第 i 个元素的能量值为 aia_iai​ 。 牛可乐可以选择至少k 个元素来施放一次魔法，魔法消耗的魔力是这些元素能量值的极差。形式化地，若所用元素编号集合为 S，则消耗的魔力为 max⁡i∈S{ai}−min⁡i∈S{ai}\max_{i\in S}\{a_i\}-\min_{i\in S}\{a_i\}maxi∈S​{ai​}...
个人笔记SpringMVC
weixin_73886232的博客
08-18 927
SpringMVC。
cursor+mcp轻松实现小红书笔记自由
2403_88996352的博客
08-17 310
跟着小妖，让你们赢在起跑线上！好用的功能太多太多，有兴趣的可以自行尝试。有提供免费的授权码可体验～有提供免费的授权码可体验～有提供免费的授权码可体验～私信小妖，获取体验码~国内可直接使用~
机试备考笔记 14/31
m0_73354184的博客
08-17 997
2025年8月14日小结：（17号整理14号的笔记，这辈子真是有了w(ﾟДﾟ)w）昨天摔了跤大的，今天好妈妈在家，松弛。省流：6道中等，明天只学了10分钟嘻嘻。
【数据库】Oracle学习笔记整理之五：ORACLE体系结构 - 参数文件与控制文件（Parameter Files & Control Files）
FixPng的博客
08-16 718
格式：分为两种类型SPFILE（服务器参数文件）：二进制格式，不可直接编辑（可 strings 查看）；PFILE（文本初始化文件）：纯文本格式，可通过文本编辑器修改。默认目录：Unix/Linux系统中默认路径为；常见名称（如）、spfile.ora（默认名称）；（如格式：二进制文件，不可通过文本编辑器直接修改；默认目录：路径由参数文件的参数指定（如常见名称：通常命名为（按副本序号区分）。
SVN服务器建站笔记（一）：公司SVN服务器部署，一版本多仓库、多版本多仓库和客户端测试
长沙红胖子Qt的技术博客
08-18 1236
本文详细介绍了在Linux服务器上搭建SVN版本控制系统的完整步骤，包括安装SVN、创建版本库、配置账号密码权限、设置authz文件、开放端口以及实现系统自启动SVN服务。重点讲解了单版本库多文件夹与多版本库两种管理方式的区别，并提供了客户端拉取代码的实用指导。文章还特别强调了SVN版本号的更新机制和权限管理的实时生效特性，为团队协作开发提供了可靠的技术支持。通过本文的指引，读者可以快速搭建并管理企业级SVN代码仓库。
Bot 流量“假阳性”调优笔记
最新发布
@云安全小杜
08-19 342
这次实验最大的收获是：与其在规则里“猜”爬虫长什么样，不如把判断逻辑外置到一个能持续学习的边缘节点。群联的清洗中心提供了实时封禁 API，让我们可以把模型结果直接落地，而不用改一行业务代码——这比传统“先打日志、再人工加黑名单”的节奏快了整整一个量级。
蓝桥杯dp蜗牛Java解析通俗
03-31
好的，用户想了解蓝桥杯动态规划题目中的“蜗牛”问题的Java解析，需要通俗易懂。首先，我需要回忆一下这道题的具体内容。通常蓝桥杯的题目名字可能不唯一，但根据常见的... dp[i] = Math.min(dp[i - 1] + a, dp[i - ...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值