1.边缘检测原理
图像边缘是图像最基本的特征,边缘在图像分析中起着重要的 作用。所谓边缘(edge)是指图像局部特征的不连续性。灰度或结构 信息的突变称为边缘,例如:灰度级的突变、颜色的突变、纹理结 构的突变。边缘是一个区域的结束,也是另一个区域的开始,利用该 特征可以分割图像。边缘检测基本思想是先检测图像中的边缘点,再按照某种策略将边缘点连接成轮廓,从而构成分割区域。由于边缘是所要提取目标和背景的分界线,提取出边缘才能将目标和背景区分开,因此边缘检测对于图像处理十分重要。
- 边缘检测算子的总结
1.Sobel算子
其主要用于边缘检测,在技术上它是以离散型的差分算子,用来运算图像亮度函数的梯度的近似值, Sobel算子是典型的基于一阶导数的边缘检测算子,由于该算子中引入了类似局部平均的运算,因此对噪声具有平滑作用,能很好的消除噪声的影响。Sobel算子对于象素的位置的影响做了加权,与Prewitt算子、Roberts算子相比因此效果更好。
Sobel算子包含2个模板,之与图像作平面卷积,即可分别得出横向及纵向的亮度差分近似值。实际使用中,常用如下两个模板来检测图像边缘。

图像的每一个像素的横向及纵向梯度近似值可用以下的公式结合,来计算梯度的大小。
G=![]()
G代表梯度,Gx为横向模板和领域的卷积,Gy为纵向模板和领域卷积。
- Roberts算子
图像空间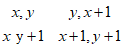
模板 

![]()
GX为横向模板和领域的卷积,Gy为纵向模板和领域卷积。
- 拉普拉斯高斯算子(LOG)
LOG算子:是高斯和拉普拉斯的双结合,即集平滑和边沿于一身的算子模型!注意这个模型跟前面的一个滤波器很相似,就是各向异性滤波器!只不过是各向异性滤波器是高斯一阶导函数,而LOG可以看做是二阶导函数!这两个模型来源最初都是因为求导导致模板对噪声干扰敏感性比较强!
可以分开求,先求出拉普拉斯边缘检测,再用高斯滤波来减少噪点。
拉普拉斯相当于二阶微分。
公式如下
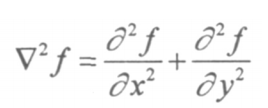
高斯卷积,函数如下
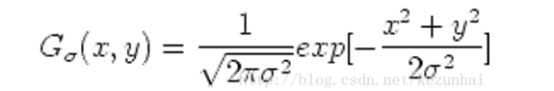
利用高斯函数可以求出高斯模板 也可以用现有模板3*3模板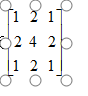
再用拉普拉斯算子边缘检测 就可以完成拉普拉斯高斯算子边缘检测
也可以结合高斯函数和拉普拉斯算子结合得出公式
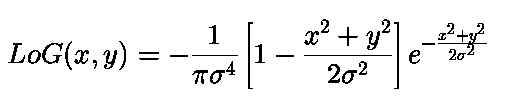
- 处理的效果展示

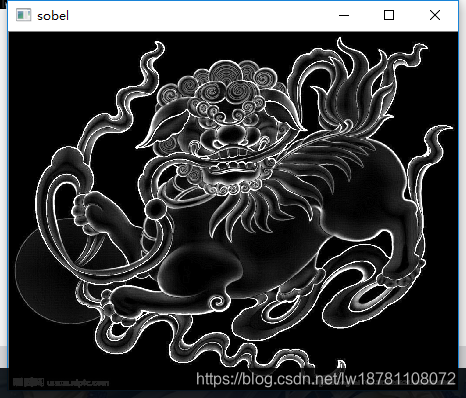

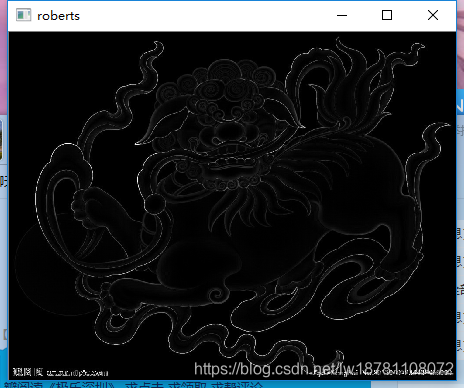




 本文深入探讨了边缘检测在图像分析中的重要性,介绍了Sobel、Roberts和LOG等经典边缘检测算子的工作原理及应用。Sobel算子通过离散型差分算子检测图像亮度函数的梯度,Roberts算子则直接计算图像空间的梯度变化,而LOG算子结合了高斯平滑和拉普拉斯边缘检测,有效减少了噪声影响。
本文深入探讨了边缘检测在图像分析中的重要性,介绍了Sobel、Roberts和LOG等经典边缘检测算子的工作原理及应用。Sobel算子通过离散型差分算子检测图像亮度函数的梯度,Roberts算子则直接计算图像空间的梯度变化,而LOG算子结合了高斯平滑和拉普拉斯边缘检测,有效减少了噪声影响。
















 9406
9406

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








