Matching In Multiplication（HDU 6073）

Matching In Multiplication

Time Limit: 6000/3000 MS (Java/Others)    Memory Limit: 524288/524288 K (Java/Others)

Total Submission(s): 1658    Accepted Submission(s): 500

Problem Description

In the mathematical discipline of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V (that is, U and V are each independent sets) such that every edge connects a vertex in U to one in V. Vertex sets U and V are usually called the parts of the graph. Equivalently, a bipartite graph is a graph that does not contain any odd-length cycles. A matching in a graph is a set of edges without common vertices. A perfect matching is a matching that each vertice is covered by an edge in the set.



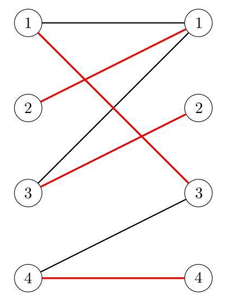
Little Q misunderstands the definition of bipartite graph, he thinks the size of U is equal to the size of V, and for each vertex p in U, there are exactly two edges from p. Based on such weighted graph, he defines the weight of a perfect matching as the product of all the edges' weight, and the weight of a graph is the sum of all the perfect matchings' weight.

Please write a program to compute the weight of a weighted ''bipartite graph'' made by Little Q.

 

Input

The first line of the input contains an integer T(1≤T≤15), denoting the number of test cases.

In each test case, there is an integer n(1≤n≤300000) in the first line, denoting the size of U. The vertex in U and V are labeled by 1,2,...,n.

For the next n lines, each line contains 4 integers vi,1,wi,1,vi,2,wi,2(1≤vi,j≤n,1≤wi,j≤109), denoting there is an edge between Ui and Vvi,1, weighted wi,1, and there is another edge between Ui and Vvi,2, weighted wi,2.

It is guaranteed that each graph has at least one perfect matchings, and there are at most one edge between every pair of vertex.

 

Output

For each test case, print a single line containing an integer, denoting the weight of the given graph. Since the answer may be very large, please print the answer modulo 998244353.

 

Sample Input

1
2
2 1 1 4
1 4 2 3

 

Sample Output

16

 //题意：一张二分图，左边每个点都是2个出度（即左边每个点都和右边的点有2条边），右边就不一定了。每2个点连一条边（一个点在左边，一个点在右边），若包含左右所有顶点，就是完美匹配。一个完美匹配的值是各边权值的乘积。现在要求所有完美匹配的值之和。

//思路：很显然，如果一个点只有1条边连向它，那么要构成完美匹配的话，这条边就一定是其中一条，（即这个点的配对点是唯一的）。且这种点一定出现在右边。先把这种情况都找出来，对于后面所有情况来说，都要包含这条边。

设满足这个条件的所有边的乘积为res。

把上述条件的那些边删去后，剩下的每个点（包括左右）必定有2条边经过。但现在的图中可能有多个环。但我们知道，在一个环中只有2种情况，设一种情况的值是v1,另一种是v2，那这个环的值就是v1+v2。我们要找出所有环，把所有环的值相乘，设为ans。

那么答案就是（ans*res）%mod。

给几组我调试的数据：

3
1 1 2 2
1 3 3 4
1 5 3 6
输出：76

4
1 4 2 1
1 4 2 3
3 4 4 1
3 4 4 3
输出：256

4
1 2 2 2
2 1 3 2
2 1 4 2
2 1 4 2
输出：16

6
1 2 2 3
2 1 3 2
2 2 3 4
3 3 4 2
5 1 6 4
5 3 6 2
输出：448

3
1 2 2 3
2 4 3 5
1 6 3 7

输出：146

#include <iostream>
#include <cstdio>
#include <cstring>
#include <string>
#include <cmath>
#include <vector>
#include <queue>
#include <algorithm>
using namespace std;

const int MAX = 600005;
const int mod = 998244353;

typedef struct {
	int val, to;
}Point;

int n;
long long sum;
vector<Point>map[MAX];
int vis[MAX];
int vis2[MAX];
int point[MAX];

void work()
{
	for (int i = 1; i <= n; i++)
		vis[i] = 1;

	//计算并删去只有1条边经过的点的情况
	int ok;
	while (true)
	{
		int i;
		ok = 0;
		for (i = n + 1; i <= 2 * n; i++)
		{
			if (map[i].size() == 1)
			{
				ok = 1;
				int v = map[i][0].to;
				vis[v] = 0;
				sum = (sum * 1LL * map[i][0].val) % mod;
				map[i].clear();
				for (int j = 0; j < map[v].size(); j++)
				{
					if (map[v][j].to != i)
					{
						int u = map[v][j].to;
						for (int k = 0; k < map[u].size(); k++)
						{
							if (map[u][k].to == v)
							{
								map[u].erase(map[u].begin() + k);
								break;
							}
						}
						break;
					}
				}
				map[v].clear();
			}
		}
		if (ok == 0)
			break;
	}


	while (true)
	{
		queue<int>q;
		long long ans = 0, cnt;
		int w, i;

		for (i = 1; i <= n; i++)
		{
			if (vis[i] == 1)
			{
				w = i;
				vis[i] = 0;
				break;
			}
		}
		if (i == n + 1)
			break;

		//找环
		int num = 0;
		point[num++] = w;
		q.push(w);
		memset(vis2, 0, sizeof(vis2));
		while (!q.empty())
		{
			int now = q.front();
			q.pop();
			for (i = 0; i < map[now].size(); i++)
			{
				if (map[now][i].to <= n && vis[map[now][i].to]==1)
				{
					vis[map[now][i].to] = 0;
					point[num++] = map[now][i].to;
					q.push(map[now][i].to);
				}
				else if (map[now][i].to > n && vis2[map[now][i].to - n] == 0)
				{
					vis2[map[now][i].to - n] = 1;
					q.push(map[now][i].to);
				}
			}
		}

		//计算环值
		for (i = 0; i < map[point[0]].size(); i++)
		{
			cnt = 1;
			cnt = (cnt * 1LL * map[point[0]][i].val) % mod;
			int xx = map[point[0]][i].to;
			int aim = point[0];
			while (true)
			{
				int now, temp;
				for (int j = 0; j < map[xx].size(); j++)
				{
					if (map[xx][j].to != aim)
					{
						now = map[xx][j].to;
						break;
					}
				}
				if (now == point[0])
					break;
				for (int j = 0; j < map[now].size(); j++)
				{
					if (map[now][j].to != xx)
					{
						cnt = (cnt * 1LL * map[now][j].val) % mod;
						temp = map[now][j].to;
					}
				}
				aim = now;
				xx = temp;
			}
			ans = (ans + cnt) % mod;
		}

		sum = (sum*ans) % mod;
	}
}

int main()
{
	int T;
	scanf("%d", &T);
	while (T--)
	{
		scanf("%d", &n);
		for (int i = 0; i <= 2*n; i++)
			map[i].clear();
		int v1, w1, v2, w2;
		for (int i = 1; i <= n; i++)
		{
			scanf("%d%d%d%d", &v1, &w1, &v2, &w2);

			//边是无向边，右边的点设为n+i
			Point a;
			a.val = w1;
			a.to = v1 + n;
			map[i].push_back(a);
			a.to = i;
			map[v1 + n].push_back(a);

			a.val = w2;
			a.to = v2 + n;
			map[i].push_back(a);
			a.to = i;
			map[v2 + n].push_back(a);

		}
		sum = 1;
		work();
		printf("%lld\n", sum%mod);
	}
	return 0;
}