【文献阅读】The HTM Spatial Pooler—A Neocortical Algorithm for Online Sparse Distributed Coding-优快云博客

The HTM Spatial Pooler—A Neocortical Algorithm for Online Sparse Distributed Coding

Yuwei Cui, Subutai Ahmad* and Jeff Hawkins
Numenta, Inc., Redwood City, CA, United States

摘要

层级时间记忆（HTM）提供了一个理论框架，可模拟新皮质的若干关键计算原理。本文中，我们分析了HTM的一个重要组件——HTM空间池化器（SP）。SP模拟神经元如何学习前馈连接并形成高效的输入表征，它结合竞争性赫布学习规则和稳态兴奋性控制，将任意二进制输入模式转换为稀疏分布式表征（SDRs）。我们阐述了SP的多项关键特性，包括对输入统计量变化的快速适应、通过学习提升的噪声鲁棒性、细胞的高效利用以及对细胞死亡的耐受性。为量化这些特性，我们提出了一组可直接通过SP输出计算的指标，并通过针对性的人工模拟验证了这些特性的满足情况。随后，我们在完整的端到端真实世界HTM系统中验证了SP的价值，并探讨了其与神经科学及以往稀疏编码研究的关联。HTM空间池化器是一种受神经启发的算法，能够以在线方式从含噪数据流中学习稀疏表征。

关键词：层级时间记忆；空间池化器；稀疏编码；竞争性学习；赫布学习；在线学习；稀疏分布式表征

引言

我们的大脑通过外周传感器持续接收大量关于外部世界的信息，这些传感器将光亮度、声压和皮肤形变的变化转化为数百万个尖峰序列。每个皮质神经元都需要通过与部分突触前神经元形成突触连接，来理解大量时变输入。神经元群体的集体激活模式参与构成了我们的感知和行为。神经科学的核心问题之一是，单个皮质神经元如何学习对特定输入尖峰模式做出响应，以及神经元群体如何以灵活、动态且稳健的方式共同表征输入的特征。

层级时间记忆（HTM）是一个模拟新皮质多项结构和算法特性的理论框架（Hawkins等人，2011）。HTM网络采用包含非线性活性树突的真实神经元模型（Antic等人，2010；Major等人，2013），该模型具有数千个突触（Hawkins和Ahmad，2016），能够以连续在线的方式学习基于时间的序列。应用于流数据时，HTM网络在异常检测（Lavin和Ahmad，2015；Ahmad等人，2017）和序列预测任务（Cui等人，2016a）中实现了最先进的性能。

HTM的成功依赖于稀疏分布式表征（SDRs）的使用（Ahmad和Hawkins，2016）。这种稀疏编码是局部编码和密集编码之间的理想折中（Földiák，2002），既能同时表征不同项目且干扰极小，又能保持较大的表征容量（Kanerva，1988；Ahmad和Hawkins，2015）。已有研究证实，SDRs存在于听觉、视觉和体感皮质区域（Vinje和Gallant，2000；Weliky等人，2003；Hromádka等人，2008；Crochet等人，2011）。HTM空间池化器（SP）是HTM网络的核心组件，能够将感觉输入流持续编码为SDRs。该术语最初在Hawkins等人（2011）的研究中提出，之所以称为“空间池化器”，是因为具有大量共激活神经元（即空间相似）的输入模式会被分组为共同的输出表征。近年来，人们对HTM空间池化器的数学特性（Pietron等人，2016；Mnatzaganian等人，2017）及其基于机器学习的应用（Thornton和Srbic，2013；Ibrayev等人，2016）的兴趣日益浓厚。本文中，我们将探索HTM空间池化器的若干尚未被系统分析的功能特性。

HTM空间池化器融合了新皮质的多项计算原理，包括竞争性赫布学习（Hebb，1949）、稳态兴奋性控制（Davis，2006）、感觉皮质的连接拓扑（Udin和Fawcett，1988；Kaas，1997）以及活性依赖的结构可塑性（Zito和Svoboda，2002）。HTM空间池化器的设计目标是实现一组支持下游SDR计算的特性，具体包括：（1）通过将相似输入映射到相似输出来保留输入空间的拓扑结构；（2）持续适应输入流的统计量变化；（3）形成固定稀疏度的表征；（4）具有噪声鲁棒性；（5）具有容错性。作为HTM的核心组件，SP的输出易于被下游神经元识别，有助于提升端到端HTM系统的性能。

本文的主要目标是深入探讨HTM空间池化器的计算特性，并验证其在端到端HTM系统中的价值。文章结构如下：首先介绍HTM空间池化器算法；详细讨论其计算特性，并提出量化这些特性的指标；通过特定的独立模拟和端到端HTM系统场景，验证这些特性的满足情况；最后探讨潜在的神经机制以及与现有稀疏编码技术的关联。

模型

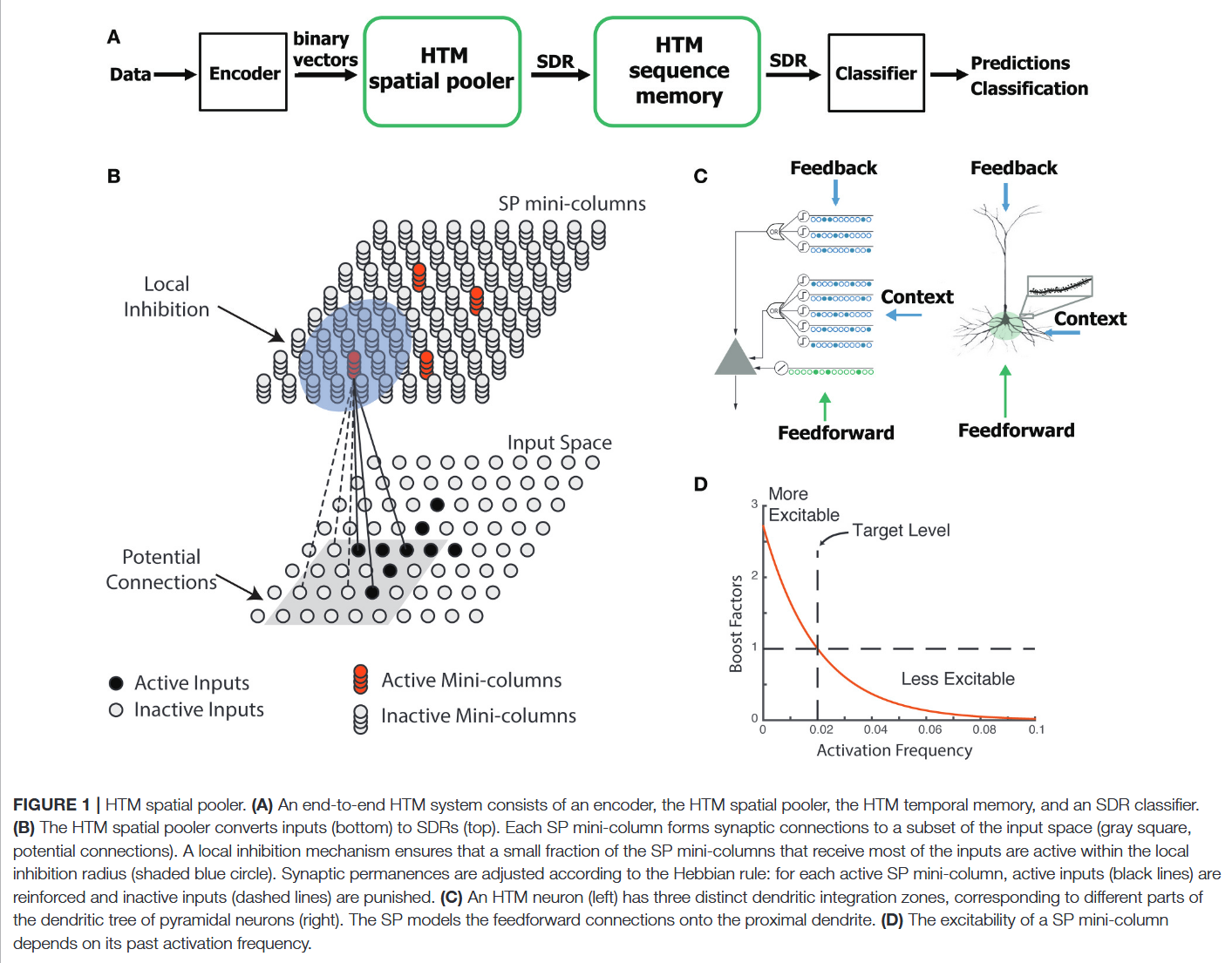
在这里插入图片描述

SP是HTM网络的核心组件（图1A）。在端到端HTM系统中，SP以连续在线的方式将输入模式转换为SDRs。HTM时间记忆学习这些SDRs的时间序列，并对未来输入进行预测（Cui等人，2016a；Hawkins和Ahmad，2016）。HTM网络的单个层级由一组迷你柱构成，每个迷你柱包含多个细胞（图1B）。HTM神经元模型融合了新皮质锥体细胞的树突特性（Spruston，2008），其中HTM神经元的近端和远端树突段具有不同功能（图1C）（Hawkins和Ahmad，2016）。近端树突检测到的模式会引发动作电位，定义神经元的经典感受野；远端突触识别的模式则通过使细胞去极化（但不直接引发动作电位）发挥预测作用。

在HTM理论中，同一迷你柱内的不同细胞在不同时间语境下表征前馈输入。SP模拟近端树突段的突触生长，由于同一迷你柱内的细胞共享相同的前馈经典感受野（Buxhoeveden，2002），SP模拟了这种共同感受野如何从输入中学习。SP的输出表征迷你柱对前馈输入的激活情况；HTM时间记忆模拟细胞的远端树突段，并通过根据时间语境激活不同细胞组来学习SDRs的转换（Hawkins和Ahmad，2016），其输出表征所有迷你柱中单个细胞的激活情况。

SP模拟相邻迷你柱之间的局部抑制，这种抑制实现了k-胜者全取计算（Majani等人，1988；Makhzani和Frey，2015）。在任意时刻，只有输入激活最强的一小部分迷你柱会处于激活状态。每个时间步长内，活跃细胞的前馈连接会根据赫布学习规则进行调整。稳态兴奋性控制机制则在较慢的时间尺度上运作，该机制在Hawkins等人（2011）的研究中被称为“增强（boosting）”，因为它能提高激活不足的迷你柱的相对兴奋性，鼓励连接不足的神经元激活并参与输入表征。

每个SP迷你柱与一组输入神经元形成突触连接。假设输入神经元在输入空间中按拓扑结构排列，用 $x_{j}$ 表示第j个输入神经元的位置，用二进制变量 $z_{j}$ 表示其激活状态。输入空间的维度取决于具体应用：例如，输入为图像时维度为二维，输入为标量时维度为一维。已有多种编码器可用于处理不同数据类型（Purdy，2016）。输出神经元同样在不同空间中按拓扑结构排列，用 $y_{i}$ 表示第i个SP迷你柱的位置。

SP中采用HTM神经元模型（图1B），该模型的设计动机和支持证据详见Hawkins和Ahmad（2016）的研究。该模型的学习规则受神经科学中活性依赖突触发生研究的启发（Zito和Svoboda，2002）。第i个SP迷你柱的突触位于输入空间中以 $x_{i}^{c}$ 为中心、边长为γ的超立方体内，每个SP迷你柱与该区域内的部分输入形成潜在连接。之所以称为“潜在”连接，是因为只有当突触持久性超过连接阈值时，突触才会实际连接。第i个迷你柱的潜在输入连接初始化如下：
$Πi={j∣I(xj;xic,γ)andZij<p}\Pi_{i}=\left\{j | I\left(x_{j} ; x_{i}^{c}, \gamma\right) and Z_{i j}<p\right\}$
其中， $I(xj;xic,γ)I(x_{j} ; x_{i}^{c}, \gamma)$ 是指示函数，仅当 $x_{j}$ 位于以 $x_{i}^{c}$ 为中心、边长为γ的超立方体内时返回1； $Z_{i j} ~ U(0,1)$ 是[0,1]区间内均匀分布的随机数；p是超立方体内成为潜在连接的输入比例。潜在连接仅初始化一次，在学习过程中保持固定。

我们用标量持久性值表征每个突触，当持久性值高于连接阈值时，认为突触处于连接状态。用二进制矩阵W表示连接突触的集合：
$Wij={1ifDij≥θc0otherwiseW_{i j}=\left\{\begin{array}{c}1 if D_{i j} \geq \theta_{c} \\ 0 otherwise \end{array}\right.$
其中， $D_{i j}$ 表示第j个输入到第i个SP迷你柱的突触持久性，其取值范围为0到1。潜在突触的持久性初始化为[0,1]区间内的独立同分布均匀随机数：
$Dij={U(0,1)ifj∈Πi0otherwiseD_{ij}=\left\{\begin{array}{cc} U(0,1) & if j \in \Pi_{i} \\ 0 & otherwise \end{array}\right.$

所有实验中，连接阈值 $θc\theta_{c}$ 均设为0.5，因此初始时50%的潜在突触处于连接状态。SP的性能对连接阈值参数不敏感。

相邻SP迷你柱通过局部抑制机制相互抑制，第i个SP迷你柱 $y_{i}$ 的邻域定义为：
$Ni={j∣∥yi−yj∥<ϕ,j≠i}N_{i}=\left\{j |\left\| y_{i}-y_{j}\right\| <\phi, j \neq i\right\}$
其中， $∥yi−yj∥\left\|y_{i}-y_{j}\right\|$ 是迷你柱i和j之间的欧氏距离。局部抑制在输入空间具有拓扑结构（即相邻输入神经元表征输入空间相似子区域的信息）时尤为重要。抑制半径会动态调整，以确保局部抑制作用于接收同一输入区域信息的迷你柱——平均感受野尺寸增大时，φ也会增大。具体而言，φ由所有SP迷你柱的平均连接输入跨度与每个输入对应的迷你柱数量的乘积决定。若SP输入和迷你柱维度相同，初始时 $ϕ=γ\phi=\gamma$ 。在实际应用中，我们也会处理无自然拓扑结构的输入空间（如分类数据）（Purdy，2016），此时输入无自然排序，我们使用无穷大的φ实现全局抑制。

给定输入模式z，SP迷你柱的激活状态通过以下步骤确定：首先计算每个迷你柱的前馈输入（称为输入重叠）：
$oi=bi∑jWijzjo_{i}=b_{i} \sum_{j} W_{i j} z_{j}$
其中， $b_{i}$ 是控制每个SP迷你柱兴奋性的正增强因子。

当前馈输入高于刺激阈值 $θstim\theta_{stim}$ 且属于其邻域内前s%的迷你柱时，该SP迷你柱被激活：
$ai={1ifoi≥Z(Vi,100−s)andoi≥θstim0otherwisea_{i}=\left\{\begin{array}{c}1 if o_{i} \geq Z\left(V_{i}, 100-s\right) and o_{i} \geq \theta_{stim } \\ 0 otherwise \end{array}\right.$

通常将 $θstim\theta_{stim}$ 设为较小的正值，以防止输入不足的迷你柱被激活。 $Z (X, p)$ 是百分位函数，返回数据向量X中对应百分比p（区间[0,100]）的分位数； $V_{i}$ 是第i个迷你柱所有相邻迷你柱的重叠值集合：
$Vi={oj∣j∈Ni}V_{i}=\{ o_{j}|j\in N_{i}\}$
s是目标激活密度（通常设为2%）。激活规则（公式6-7）在局部邻域内实现k-胜者全取计算，已有研究表明，这种计算可通过具有精确尖峰时序的整合-发放神经元模型实现（Billaudelle和Ahmad，2015）。本研究中，为加快模拟速度，我们采用离散时间步长。

前馈连接通过赫布规则学习：对于每个活跃的SP迷你柱，活跃的输入连接通过增加 $p^{+}$ 的突触持久性得到强化，而不活跃的连接则通过减少 $p^{-}$ 的突触持久性受到抑制。突触持久性被限制在0和1的范围内。

增强因子的更新方式为：将每个迷你柱的近期活性与其邻域的近期活性进行比较。计算每个迷你柱在过去T个输入上的时间平均激活水平：
$a‾i(t)=(T−1)∗a‾i(t−1)+ai(t)T\overline{a}_{i}(t)=\frac{(T-1) * \overline{a}_{i}(t-1)+a_{i}(t)}{T}$
其中， $a_{i}(t)$ 是第i个迷你柱在时间t的当前活性；T控制增强因子的更新速度。由于活性具有稀疏性，需要多个步骤才能获得有意义的激活水平估计，通常选择T=1000。公式（8）中的时间平均激活水平可通过对电压信号或细胞内钙浓度进行低通滤波近似，类似计算已用于以往的稳态突触可塑性模型（Clopath等人，2010；Habenschuss等人，2013）。

迷你柱邻域的近期活性计算如下：
$<a‾i(t)>=1∣Ni∣∑j∈Nia‾j(t)<\overline{a}_{i}(t)>=\frac{1}{\left|N_{i}\right|} \sum_{j \in N_{i}} \overline{a}_{j}(t)$

最后，基于 $a‾i(t)\overline{a}_{i}(t)$ 与 $<a‾i(t)><\overline{a}_{i}(t)>$ 的差值更新增强因子 $b_{i}$ （图1D）：
$bi=e−β(a‾i(t)−<a‾i(t)>)b_{i}=e^{-\beta\left(\overline{a}_{i}(t)-<\overline{a}_{i}(t)>\right)}$

其中，β是控制适应效应强度的正参数。上述增强机制受神经元兴奋性稳态调节研究的启发（详见Davis，2006的综述），通过提高平均发放率不足的迷你柱的增益，鼓励迷你柱的高效利用。具体公式并非关键，我们选择公式（10）是因其简洁性。

在这里插入图片描述

结果

HTM空间池化器的特性

本节将阐述HTM空间池化器的一组理想特性，这些特性确保了对统计量变化的输入流进行灵活且稳健的表征，对下游神经计算至关重要。

SP的第一个特性是形成固定稀疏度的输入表征。为支持下游神经计算，SP的输出必须能被下游神经元识别。皮质神经元通过引发非线性树突尖峰（Major等人，2013）或体细胞动作电位（Bean，2007）识别突触前输入模式，其阈值取决于细胞的内在特性。已有研究表明，若突触前输入具有固定的稀疏度水平，突触前激活模式的识别将更稳健可靠（Ahmad和Hawkins，2016）。但若稀疏度高度可变，高激活密度的输入模式更可能引发下游神经元的树突尖峰或动作电位，而低激活密度的模式则难以被检测，这将导致高密度模式的假阳性错误和低密度模式的假阴性错误。固定稀疏度的优势在于，它能确保所有输入模式都能被平等检测。

第二个理想特性是系统应利用所有可用资源学习输入的最优表征。从信息论角度来看，几乎始终活跃或对任何输入模式都无响应的神经元，对输入的信息传递贡献极小。在神经元数量有限的情况下，理想状态是每个神经元对一部分输入做出响应，从而所有神经元都参与输入空间的表征。SP中的增强机制（公式8-10）正是为实现这一目标而设计，我们通过熵指标量化该特性（详见下文）。

第三个理想特性是输出表征应对输入噪声具有稳健性。现实世界中的数据往往存在噪声，传感器噪声、数据传输错误和设备固有局限性都可能导致数据不准确或缺失。在大脑中，感觉神经元对特定刺激的响应可能存在显著差异（Tolhurst等人，1983；Faisal等人，2008；Masquelier，2013；Cui等人，2016b）。因此，SP必须具备良好的噪声鲁棒性，确保输入的微小变化不会显著影响输出表征。

第四个特性是系统应具有灵活性，能够适应输入统计量的变化。新皮质具有高度的灵活性和可塑性，其区域能通过调整以表征输入数据变化后的不同输入。若输入数据的统计量发生变化，SP应通过调整突触连接快速适应新数据。该特性在处理统计量快速变化的连续数据流应用中尤为重要（Cui等人，2016a）。

最后一个特性是系统应具有容错性。若新皮质的部分区域受损（如中风或创伤性脑损伤），感知能力和运动功能通常会先出现缺陷，但在损伤后的数周至数月内会显著恢复（Nudo，2013）。已有研究表明，传入输入的限制性损伤（如视网膜损伤）后，感觉神经元的感受野会发生重组（Gilbert和Wiesel，1992；Baker等人，2005）。因此，当网络中出现输入或输出神经元丢失等系统故障时，SP应仍能正常运作。

空间池化器指标

除了评估端到端HTM系统的性能外，我们还希望量化SP作为独立组件的表现。由于SP是一种旨在实现多项特性的无监督算法，我们提出了一组可直接基于SP输入和输出计算的统计指标。这些指标在SP配置导致端到端HTM系统性能不佳时尤为实用。

指标1：稀疏度

定义群体稀疏度为：
$st=1N∑i=1Naits^{t}=\frac{1}{N} \sum_{i=1}^{N} a_{i}^{t}$
其中， $a_{i}^{t}$ 是第i个迷你柱在时间步t的活性，N是SP迷你柱的数量。该指标反映每个时间步长内活跃神经元的百分比，由于我们采用二进制激活（公式6），稀疏度的计算较为直接。该指标与其他用于标量值激活的群体稀疏度指标原理一致（Willmore和Tolhurst，2001）。通过观察不同时间稀疏度的标准差，可量化SP实现固定稀疏度的效果。

指标2：熵

给定M个输入的数据集，每个SP迷你柱的平均激活频率为：
$P(ai)=1M∑t=1MaitP\left(a_{i}\right)=\frac{1}{M} \sum_{t=1}^{M} a_{i}^{t}$

第i个SP迷你柱的熵由二进制熵函数给出：
$S_{i}=-P(a_{i}) log_{2} P(a_{i})-(1-P(a_{i}))log _{2}(1-P(a_{i}))$

按照惯例，若 $P(a_{i})$ 等于0或1，则设 $S_{i}=0$ 。定义空间池化器的熵为：
$S=∑i=1NSiS=\sum_{i=1}^{N} S_{i}$

由于SP的平均稀疏度几乎恒定，当所有SP迷你柱的激活频率相等时，熵达到最大值。若少数SP迷你柱频繁激活而其余迷你柱几乎不激活，SP的熵将较低。因此，熵指标可量化SP对所有迷你柱的利用效率。

指标3：噪声鲁棒性

通过测量SP表征对不同输入噪声水平的敏感性来测试噪声鲁棒性。将干净输入和受噪声污染的输入分别记为 $z_{i}$ 和 $z_{i}'(k)$ （k表示添加到输入中的噪声量），对应的SP输出分别记为 $a_{i}$ 和 $a_{i}'(k)$ 。模拟中，我们随机将k%的活跃输入位翻转为不活跃，并将相同数量的不活跃输入位翻转为活跃——该过程在保持输入稀疏度恒定的同时使输入随机化。噪声水平在0%到100%之间变化，测量SP输出中共享活跃迷你柱的比例（对M个输入取平均）。噪声鲁棒性指数定义为：
$R=1M∑i=1M∫k=01∥ai∘ai′(k)∥0∥ai∥0dkR=\frac{1}{M} \sum_{i=1}^{M} \int_{k=0}^{1} \frac{\left\| a_{i} \circ a_{i}'(k)\right\| _{0}}{\left\| a_{i}\right\| _{0}} d k$

L0范数∥·∥₀表示二进制向量中非零位的数量；∘运算符表示元素-wise乘法。注意，对于二进制向量，L0范数与L1范数相同。噪声鲁棒性指数测量图2C中输出重叠曲线下的面积：当噪声为0时，共享活跃迷你柱的比例为100%，随着噪声量增加逐渐降至0，因此噪声鲁棒性的取值范围为0到1。

指标4：稳定性

由于SP是持续学习的系统，特定输入的表征可能会随时间变化或变得不稳定。输入统计量未变时的不稳定性可能会对下游过程产生负面影响。我们通过定期禁用学习并呈现固定的随机输入子集来测量稳定性：稳定性指数是每个输入中保持恒定的活跃迷你柱的平均比例。

将第j个测试点对第i个测试输入的SP输出记为 $a_{i}^{j}$ ，则测试点j的稳定性指数为：
$T(j)=1M∑i=1M∥aij∘aij−1∥0∥aij−1∥0T(j)=\frac{1}{M} \sum_{i=1}^{M} \frac{\left\| a_{i}^{j} \circ a_{i}^{j-1}\right\| _{0}}{\left\| a_{i}^{j-1}\right\| _{0}}$

其中，M是测试输入的数量。稳定性的取值范围为0到1，完全稳定的SP的稳定性指数为1。注意，公式（16）中的上标j是测试点的索引，而非时间步长。我们计算连续测试点之间相同测试输入的SP输出重叠百分比，并在测试点之间用全部训练数据训练SP。

模拟细节

我们进行了多项不同的模拟（数据集描述如下）：对于具有拓扑结构的实验，使用32×32个迷你柱的二维SP；对于无拓扑结构的实验，使用1024个迷你柱的无量纲SP。SP的完整参数集如表1所示，所有实验的源代码可在以下链接获取：https://github.com/numenta/htmpapers。
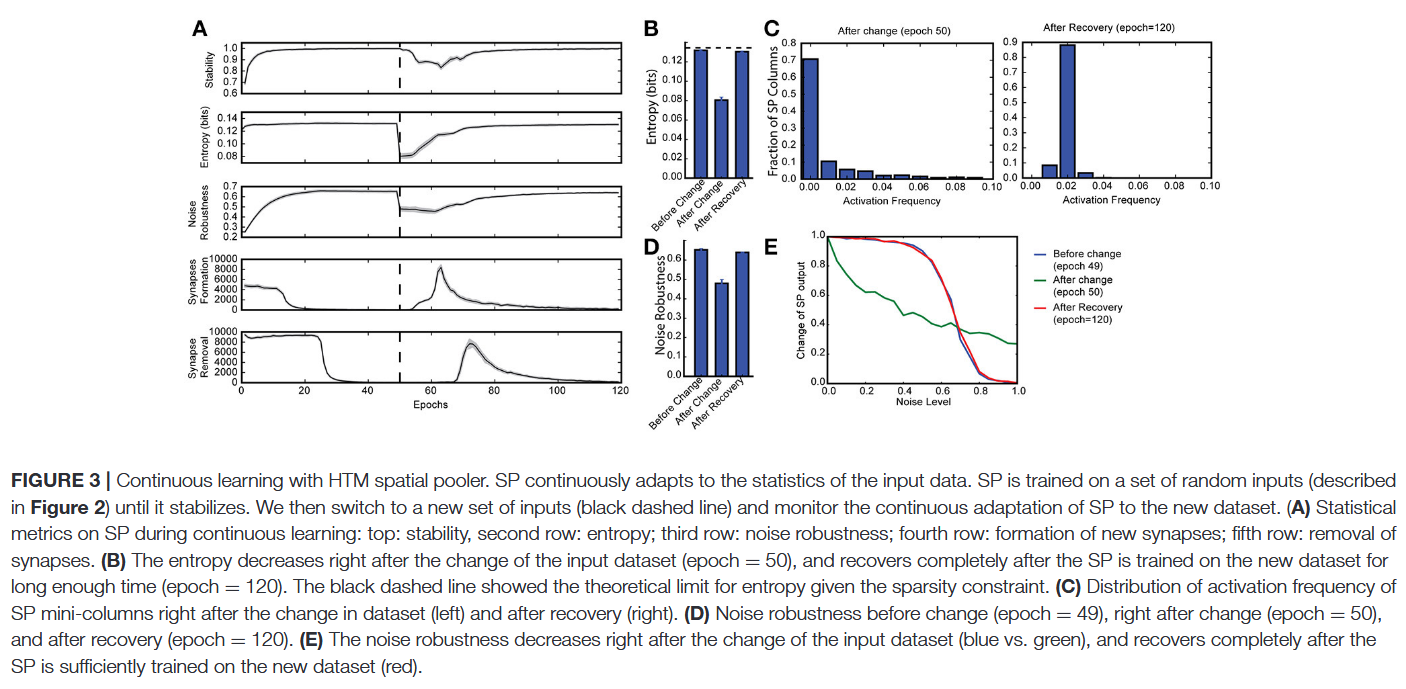
在这里插入图片描述

表1 | HTM空间池化器的参数

通用参数	数值
激活密度	2%
突触持久性连接阈值θₙ	0.5
突触持久性增量p⁺	0.1
突触持久性减量p⁻	0.02
增强强度β	100
激活频率占空比T	1000
刺激阈值θₛₜᵢₘ	1
潜在输入比例p	1
一维空间池化器参数（无拓扑结构）
迷你柱维度	1024×1
潜在输入半径γ	∞
二维空间池化器参数（有拓扑结构）
迷你柱维度	32×32
潜在输入半径γ	5

所有数据集均以流式在线方式呈现，每个数据集被呈现给SP一次或多次。我们将“轮次（epoch）”定义为随机顺序遍历整个数据集一次——该轮次定义与批量训练范式不同，因为SP每次接收一个输入模式，不保留整个数据集的缓冲区。我们在轮次之间用随机输入子集（禁用学习）测量SP指标，实际应用中也可在学习过程中持续监测这些指标。

使用的数据集如下：

随机稀疏输入：创建100个不同稀疏度水平的随机输入，每个输入是32×32的图像，其中少数位为活跃状态，活跃输入的比例在2%到20%之间均匀选择。该数据集采用具有拓扑结构的SP，用于图2和图3的实验。
随机条带和十字形：随机条带数据集包含100对随机条带，每个随机条带对刺激是10×10的图像，包含随机位置的水平条带和垂直条带（条带长度为5个像素）；随机十字形数据集包含100个随机位置的十字形模式，每个十字形由中心相交的水平条带和垂直条带组成（条带长度为5个像素）。该数据集用于图4A和图4B的实验。
MNIST：在MNIST手写数字数据库（Lecun等人，1998）上训练无拓扑结构的SP，将60000个训练样本以单轮次呈现给SP。训练后，可视化随机选择的部分SP迷你柱的感受野结构，该数据集用于图4C的实验。
具有拓扑结构的容错性实验：容错性实验（图5）使用随机条带集图像作为输入，输入空间维度为32×32，每个输入包含6个随机位置的水平或垂直条带（条带长度为7个像素）。采用具有二维拓扑结构的SP（32×32个迷你柱），首先在随机条带输入上训练完整的SP直至稳定（18000个输入后），然后测试两种损伤类型：模拟中风和模拟输入损伤。模拟中风实验中，永久移除感受野中心11×11区域内的121个SP迷你柱；模拟输入损伤实验中，不改变SP，而是永久阻断输入空间的中心部分（输入空间中心11×11区域内的121个输入）。两种实验中，均再监测42000个步骤内SP的恢复情况。
纽约市出租车乘客数量预测：除上述人工数据集外，还在端到端真实世界HTM系统中测试SP，选择纽约市出租车需求预测问题。该数据集可通过纽约大都会运输署公开获取，详细信息见我们之前的研究（Cui等人，2016a）。如图1所示，输入数据流首先通过一组编码器转换为二进制表征（Purdy，2016），SP接收编码器的输出并形成SDRs，HTM序列记忆学习SDRs的序列并以稀疏时间编码表征序列，最后使用单层前馈分类网络将HTM序列记忆的输出映射为对未来输入的实时预测。该任务需在实时应用场景下建模连续流，因此SP、时间记忆和分类器均持续学习。SP输出稳健高效的表征对下游组件的学习至关重要。

参考Cui等人（2016a）的研究，我们以30分钟为间隔汇总纽约市出租车的乘客数量，使用标量编码器和日期-时间编码器将当前乘客数量、一天中的时间和一周中的日期编码为二进制向量（Purdy，2016）。具有全局抑制的SP在编码器输出上持续训练，并为HTM序列记忆提供输入（Cui等人，2016a）。为评估SP中学习和增强机制的作用，我们比较了三种场景的预测精度：（1）无学习和增强的SP；（2）有学习但无增强的SP；（3）既有学习又有增强的SP。

模拟结果

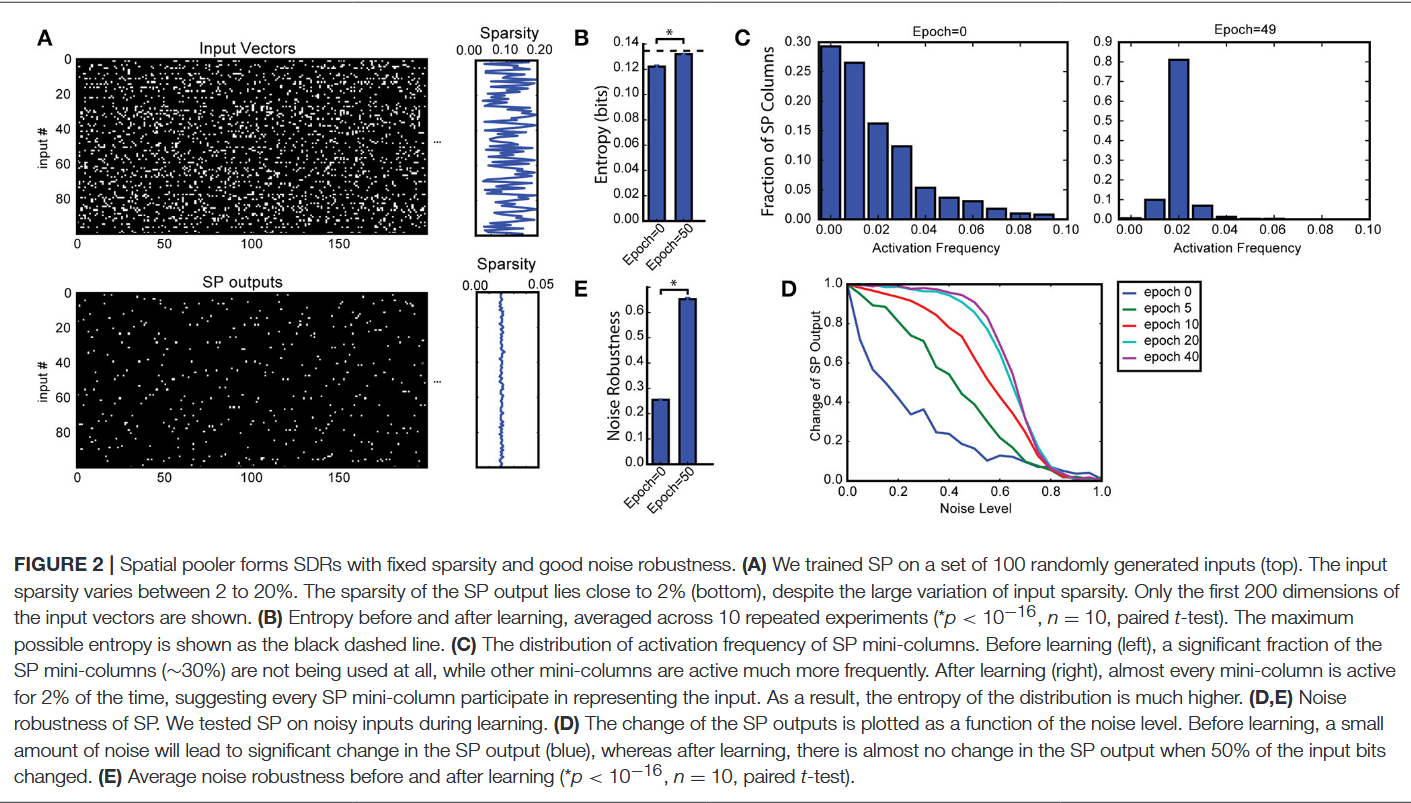
首先讨论随机稀疏输入数据集的指标结果（图2、图3）。输入模式以流式方式重复呈现给HTM空间池化器，模拟中，尽管输入稀疏度在2%到20%之间大幅变化，但SP的群体稀疏度始终接近目标水平2%（图2A）——这是网络的固有特性，源于局部k-胜者全取激活规则的使用。

我们测量了所有迷你柱的平均熵（见“空间池化器指标”部分）。由于网络的整体激活稀疏度固定，当所有迷你柱的激活概率相同时，熵达到最大值。本实验中，经过训练后，熵从0.1221±0.0013比特/迷你柱增加到0.1320±0.0007比特/迷你柱，不同随机输入集的重复实验中，该差异具有极高的统计显著性（p<10⁻⁸，n=10，配对t检验）。作为参考，相同稀疏度水平下的最大可能熵为0.1345比特/迷你柱。熵的增加源于所有迷你柱的高效利用：学习前，约30%的迷你柱对任何输入都不激活，而少数迷你柱的激活频率远高于其他迷你柱；学习后，几乎每个迷你柱的激活时间占比均为2%。

图2D和图2E展示了噪声鲁棒性随SP学习的变化。学习前，输入的微小变化会导致SP输出的显著变化，表明噪声敏感性较高（图2D，蓝色曲线）；学习后，噪声鲁棒性逐渐提升，经过40次数据集重复后，即使40%的活跃输入位发生变化，SP输出也无明显变化。平均噪声鲁棒性指数（公式15）相应地从0.254±0.004提升至0.652±0.007（图2E，p<10⁻¹⁶，n=10，配对t检验）。噪声鲁棒性的提升源于赫布学习规则：学习过程中，一组SP迷你柱与活跃输入神经元形成可靠连接，即使学习后部分输入神经元受噪声影响，仍能激活同一组SP迷你柱。

为测试SP对输入变化的适应能力，我们先训练SP直至其在一组输入上稳定，然后呈现完全不同的输入数据集（图3A）。切换到新数据集后，熵和噪声鲁棒性急剧下降（图3B、图3D），此时大量SP迷你柱对新数据集的任何输入都无响应（图3C，左图）。恢复学习后，SP快速适应新输入数据集，性能指标恢复到变化前的水平（图3B、图3D）。SP通过先形成更多新突触（图3A，第四行），然后修剪不必要的连接（图3A，第五行）来适应新数据集。这表明即使学习已稳定，SP仍能学习新数据集。需注意，由于增强规则鼓励所有迷你柱的复用，原始数据集的表征会被遗忘。

SP通过持续调整前馈连接以适应输入数据，实现上述特性。为说明SP的感受野结构如何受输入数据影响，我们在随机条带数据集上训练SP——该数据集的训练数据包括随机生成的条带对或随机位置的单个十字形。
在这里插入图片描述

图4展示了随机选择的部分SP迷你柱的感受野示例：对于该数据集，感受野通常包含随机位置的水平和垂直条带结构（图4A）。每个SP迷你柱对多个条带做出响应，以达到2%的目标激活频率；在随机十字形数据流上训练时，得到的感受野包含与输入统计量相似的十字形结构（图4B）。网络中迷你柱的数量对结果影响不大，感受野的最终结构取决于突触持久性减量与增量的比值（p⁻/p⁺）：若将p⁻增加到0.05，在随机条带对数据集上训练时，大多数感受野将包含单个条带片段（数据未展示）。

在MNIST数据集上训练SP时，感受野包含类数字结构（图4C）。尽管部分感受野明显检测单个数字，但其他感受野对多个数字做出响应——这是因为单个SP迷你柱并非“祖母细胞”（不用于检测单个输入实例），而是由一组SP迷你柱共同编码单个输入。在复杂自然数据集上训练时，预计SP内会存在多种感受野结构，这些结构可能与特定输入实例不相似。

我们还测试了SP表征混合或模糊输入的能力。在图4所用数据集上训练SP后，比较随机输入对与混合输入对的平均距离。总体而言，混合输入的SP表征与原始输入的SP表征的相似性高于与随机输入的相似性。例如，对于随机十字形数据集，两个随机输入的表征重叠度约为6.5；若创建混合输入，其SP表征与单个输入表征的重叠度跃升至约42。因此，混合输入的SP表征保留了与原始输入表征的显著相似性。

容错性

我们评估了HTM空间池化器从传入输入损伤（输入损伤实验）或部分SP迷你柱损伤（中风实验）中恢复的能力。
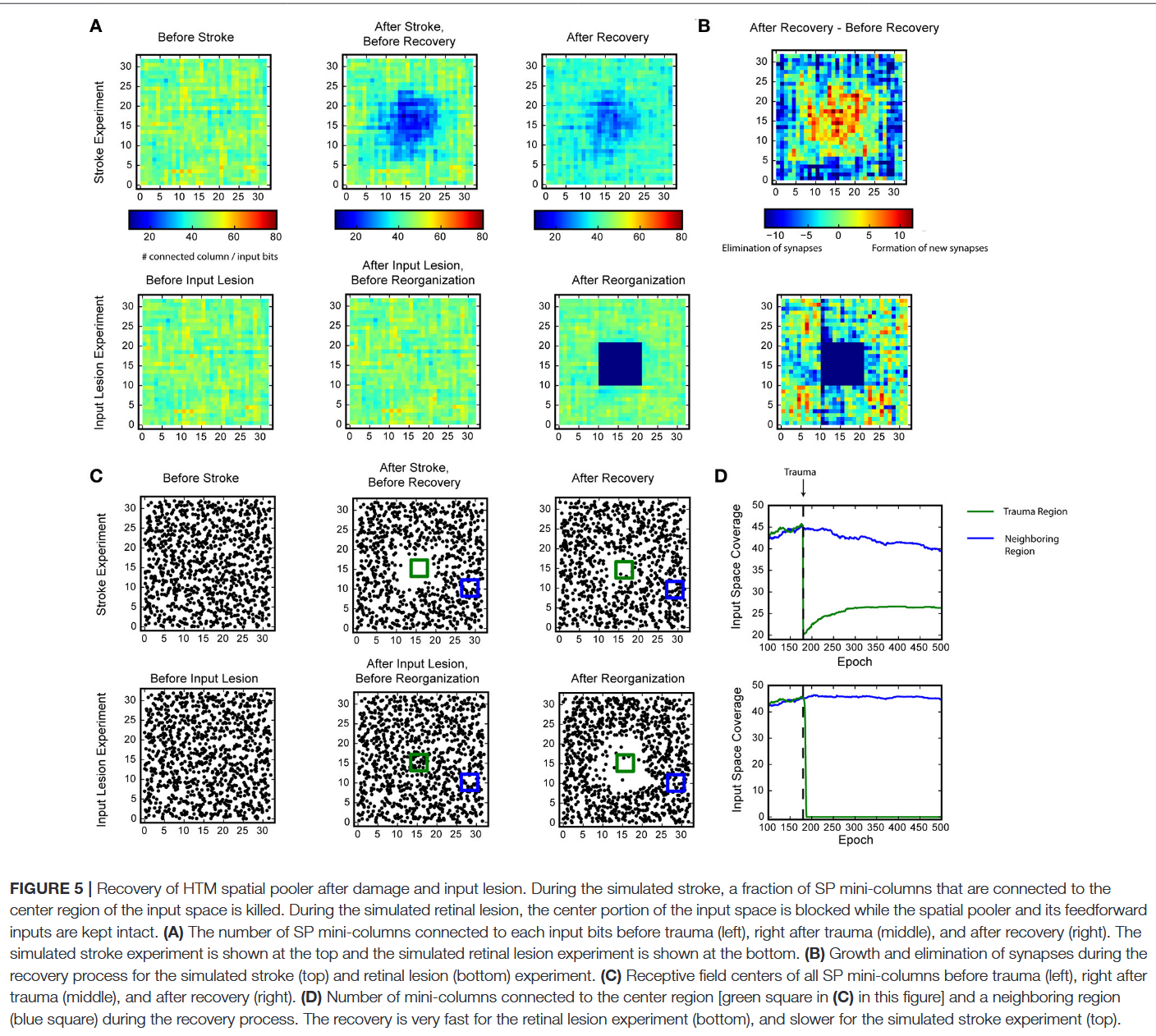
在这里插入图片描述

中风实验中，损伤后，由于对应SP迷你柱被移除，输入空间中心部分的表征大幅减少。经过数百个轮次（每个轮次包含100个输入）后，网络从损伤中部分恢复：损伤区域附近的SP迷你柱将其感受野向损伤区域转移，开始表征中心附近的刺激（图5C，补充视频1）。网络在中心区域形成更多新突触，同时损伤区域外的突触减少（图5B，上图），损伤区域的覆盖范围明显恢复（图5D，下图）。

输入损伤实验中，输入空间的中心部分被阻断。由于SP迷你柱及其相关突触连接未发生变化，输入空间覆盖范围（图5A，下图）或感受野中心分布（图5C，下图）无即时变化。但SP迷你柱在几个轮次内快速重组其感受野：对中心输入做出响应的SP迷你柱开始对周围未损伤区域的输入做出响应（图5C，补充视频2）。重组后，几乎所有与损伤区域的连接都消失（图5B，下图）。

这些结果证明了SP的容错性和灵活性。SP的固定稀疏度和稳态兴奋性控制机制确保输入空间能被所有（未损伤的）SP迷你柱高效表征。值得注意的是，两种模拟中不同的恢复速度与实验研究结果一致：已有研究报道，双眼视网膜局灶性损伤后，位于视网膜盲点边缘的皮质神经元的感受野尺寸在几分钟内增大（Gilbert和Wiesel，1992）；相比之下，若新皮质部分区域受损，恢复是部分性的，且时间尺度慢得多（Nudo，2013）。

实时流分析任务中的空间池化器

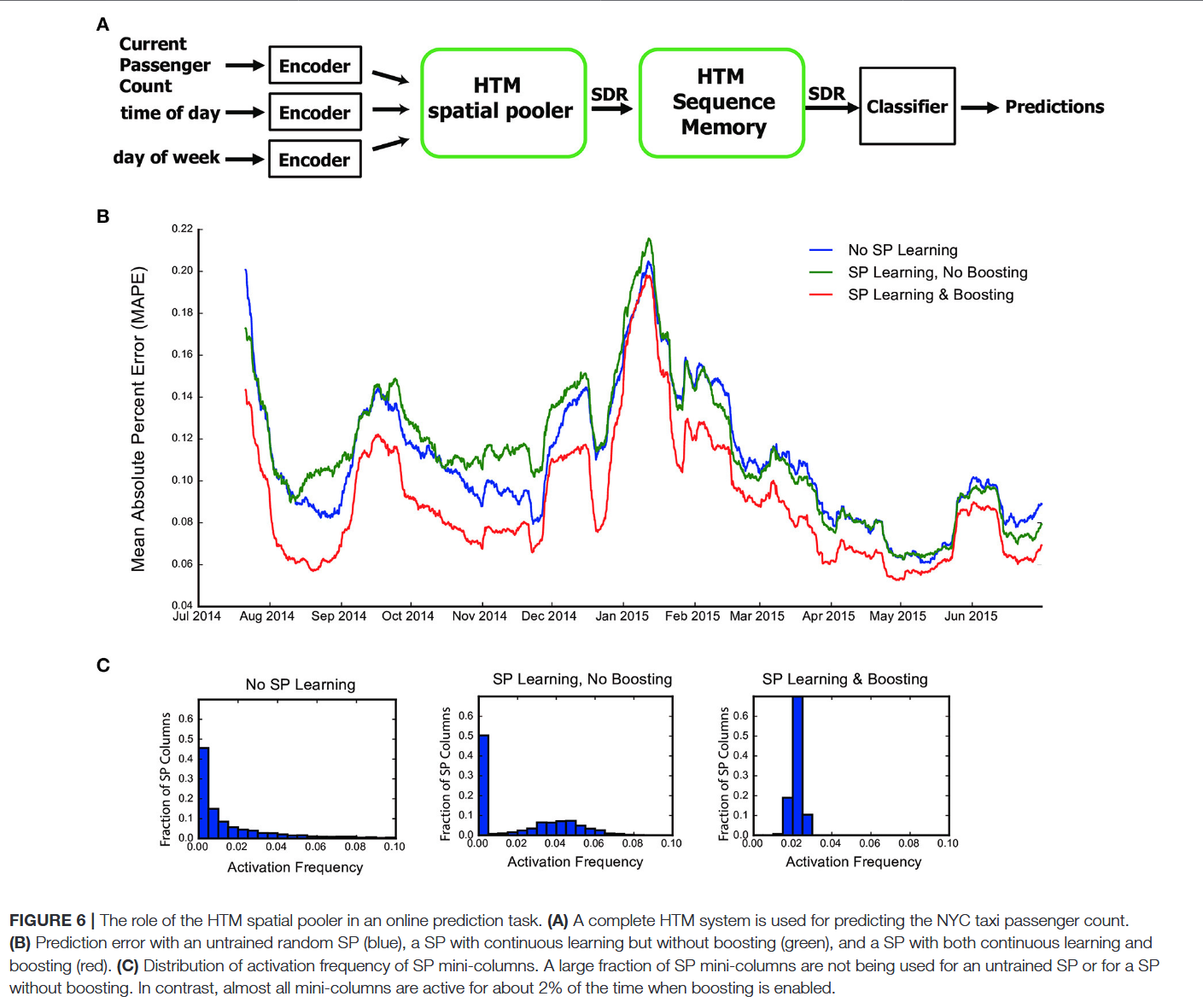
在这里插入图片描述

本节评估SP在端到端真实世界HTM系统中的作用，以纽约市出租车乘客数量的实时预测问题为例（图6A，见“方法”部分）。我们之前的研究表明，带有固定预训练SP的HTM系统在该任务上实现了最先进的性能（Cui等人，2016a）。本文中，我们探讨SP中学习的作用，并评估三种场景：使用随机初始化且无学习的SP、允许SP学习但无增强（增强强度设为0）、使用既有持续学习又有增强（增强强度设为100）的SP。

我们以单次传递的方式输入数据，模拟实时在线预测场景。三种场景的时间平均预测误差随训练时间的变化如图6B所示：学习初期，预测误差快速下降，代表系统的初始学习阶段；误差的偶尔上升反映了现实世界中的变化（如感恩节、圣诞节、纽约市马拉松等事件和假期）。

既有学习又有增强的SP在整个预测任务中表现最佳；有学习但无增强的SP与随机静态SP的性能大致相当，这表明持续赫布学习和稳态兴奋性控制均至关重要。通过观察SP迷你柱的激活频率分布可理解性能差异：无稳态兴奋性控制时，大量SP迷你柱未被利用（图6C），HTM序列记忆学习此类表现不佳的SDRs转换时更易出错。

讨论与结论

本文中，我们阐述了HTM空间池化器的特性——这是一种受神经启发、用于在线学习SDRs的算法。HTM空间池化器的设计灵感源于新皮质的计算原理，目标是创建SDRs并支持序列学习和记忆等基本神经计算。该模型满足多项重要特性，包括对输出稀疏度的严格控制、迷你柱的高效利用、输入相似性的保留、噪声鲁棒性、容错性和快速适应性。这些特性通过竞争性赫布学习规则和稳态兴奋性控制机制实现。我们在端到端HTM系统的流数据预测任务中验证了SP的有效性，表明HTM空间池化器构建了一种可用于实际机器学习应用的灵活稀疏编码方案。

与其他稀疏编码技术的关联

SP为输入学习SDRs，属于稀疏编码技术的广泛类别——这类技术通过少数神经元的激活来编码每个项目。稀疏编码的一种理论认为，感觉皮质中的稀疏激活在保留大部分信息的同时降低了大脑的能量消耗（Földiák，2002；Olshausen和Field，2004）。早期稀疏编码研究明确优化了结合低重建误差和高稀疏度的成本函数（Olshausen和Field，1996a，1997）。将这些技术应用于自然图像时，得到的感受野与V1神经元的感受野相似（Olshausen和Field，1996a；Lee等人，2006），表明早期感觉神经元的功能可通过稀疏编码框架解释。已有研究通过生物学上合理的局部学习规则实现了稀疏编码，Földiák发现，神经网络可通过赫布前馈连接结合局部阈值控制机制学习稀疏编码（Földiák，1990），近期研究表明此类学习规则可通过解析推导得出（Hu等人，2014）。

本文分析的多项特性在以往的稀疏编码研究中也有讨论：已有研究表明，稀疏表征天然具有噪声鲁棒性，可用于稳健语音识别（Sivaram等人，2010；Gemmeke等人，2011）、稳健人脸识别（Wright等人，2009）和超分辨率图像重建（Yang等人，2010）。为处理动态数据集，已有研究提出了在线稀疏编码和字典学习技术（Mairal等人，2010）。已知传统稀疏编码技术学习的表征熵较低，因为输出单元的活性概率分布在零附近达到峰值，且具有重尾特性（Olshausen和Field，1996b）。本研究发现，尽管与密集表征相比，HTM空间池化器的熵较低，但训练后熵会增加——这是因为稳态兴奋性控制机制鼓励SP中的神经元具有相似的激活频率，从而提高了网络的表征能力。

以往大多数研究认为，稀疏编码的目标是避免信息丢失、降低能量消耗并形成交叉干扰最小的联想记忆（Olshausen和Field，2004）。常用的评价标准是，给定稀疏激活和一组学习到的基向量，输入的重建效果如何。尽管这些研究解释了初级视觉皮质的感受野结构，并催生了用于特征选择（Gui等人，2016）和数据压缩（Pati等人，2015）的实用机器学习算法，但神经计算的目的不仅仅是保留信息。本文采用不同视角，探讨HTM空间池化器的计算特性如何在HTM系统中支持下游皮质处理。我们不使用重建误差，而是通过一组特性（包括群体熵、噪声鲁棒性、稳定性和容错性）定义SP的性能。对SP进行多维度评估至关重要，这能确保其形成捕捉输入空间拓扑特性的稳健SDRs。我们的研究表明，HTM空间池化器满足这些特性，且这些特性有助于提升端到端系统的性能。需注意，单一指标不足以确保SP正常工作：例如，始终使用少量SP迷你柱可实现良好的噪声鲁棒性，但会导致熵值不佳；每个时间步长使用随机输出易实现高熵，但会导致稳定性不佳。因此，必须综合考虑所有指标，这也意味着SP的学习算法无法通过优化单一目标函数轻易推导得出。
在这里插入图片描述

HTM空间池化器的赫布学习规则与以往许多稀疏编码算法（Földiák，1990；Zylberberg等人，2011；Hu等人，2014）和联想记忆模型（Willshaw等人，1969；Hecht-Nielsen，1990；Bibbig等人，1995）相似，但存在以下差异：首先，我们将稳态兴奋性控制作为增益调制机制——稳态的作用是确保神经活性分布均匀，已有研究提出，稳态在学习稀疏表征时能提供高效解决方案（Perrinet，2010）。部分突触可塑性模型在学习规则中包含控制突触权重变化量的稳态组件（Clopath等人，2010；Habenschuss等人，2013），而SP中的稳态兴奋性调节机制无需直接影响突触修饰过程即可实现类似效果。其次，我们模拟了实现k-胜者全取计算的局部抑制电路，以严格控制输出稀疏度（图7A）——当SP激活被具有阈值非线性树突的下游神经元使用时，这一点尤为重要。我们没有像平衡网络那样明确模拟兴奋性和抑制性神经元的连续时间网络（Hansel和Mato，2013；Denève和Machens，2016），但两者的目标相似，均为维持狭窄的稀疏度范围。最后，我们使用二进制突触并通过突触发生进行学习（Zito和Svoboda，2002），二进制突触的使用可显著加快计算速度。总体而言，HTM空间池化器算法是一种适合从流数据中在线学习稀疏表征的候选方案。

空间池化器的潜在神经机制

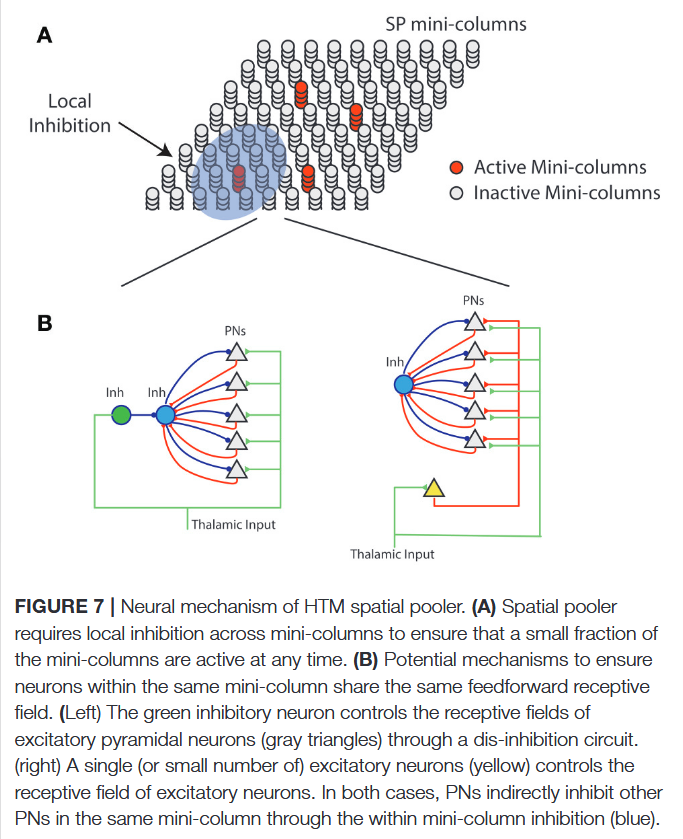
HTM系统的一个层级包含一组迷你柱，每个迷你柱内的细胞具有相同的前馈感受野。迷你柱假说已提出数十年（Mountcastle，1997；Buxhoeveden，2002），但由于缺乏理论上的优势，迷你柱的功能仍存在争议（Horton和Adams，2005）。根据HTM理论，同一迷你柱内的细胞具有相同的前馈连接但不同的侧向连接，因此在不同时间语境下表征相同的前馈输入（Hawkins和Ahmad，2016）。我们认为，SP在迷你柱水平上模拟前馈感受野学习。实验研究表明，同一迷你柱内的神经元具有几乎相同的感受野位置、尺寸和形状，而相邻迷你柱内神经元的感受野可能存在显著差异（Jones，2000）。这种变异性无法通过前馈输入的差异解释，因为单个丘脑传入纤维的分支范围（猫的分支范围可达900μm）（Jones，2000）远大于迷你柱的尺寸（直径通常为20-60μm）（Favorov和Kelly，1996；Jones，2000；Buxhoeveden，2002）。因此，需要专门的电路机制确保同一迷你柱内的细胞获得相同的感受野。

我们提出了两种可能的SP神经电路机制，并讨论了其解剖学支持：第一种机制（图7B，左图）中，前馈丘脑输入同时支配兴奋性锥体细胞和抑制性神经元（绿色），该抑制性神经元通过双突触去抑制电路间接激活锥体细胞，充当引导兴奋性神经元感受野形成的“教师细胞”。新皮质中存在多种抑制性神经元，部分类型（如双极细胞和双束细胞）仅支配皮质迷你柱内的细胞（Markram等人，2004；Wonders和Anderson，2006）。已有充分证据表明，前馈丘脑-皮质输入能强烈激活特定亚型的抑制性神经元（Gibson等人，1999；Porter等人，2001；Swadlow，2002；Kremkow等人，2016），这些抑制性神经元可能参与定义和维持皮质迷你柱的前馈感受野。

第二种机制中，单个兴奋性细胞接收丘脑输入，并支配迷你柱内的所有兴奋性细胞，该兴奋性神经元引导迷你柱内其他兴奋性细胞的感受野形成。早期发育过程中已观察到类似电路：板下神经元（一种暂时性神经元群体）接收丘脑轴突的突触输入，在丘脑轴突与其最终的IV层目标之间建立临时连接（Friauf等人，1990；Ghosh和Shatz，1992；Kanold等人，2003）。成年大脑中是否存在类似电路仍有待验证。

SP还依赖其他多种神经机制：学习规则基于竞争性赫布学习，这种学习可通过突触可塑性规则（如长时程增强（Teyler和DiScenna，1987）、长时程抑制（Ito，1989）或尖峰时序依赖可塑性（Song等人，2000））在大脑中实现；与SP增强规则类似的稳态兴奋性控制机制已在皮质神经元中观察到（Davis，2006）；最后，SP中的k-胜者全取计算可通过漏整合-发放神经元模型实现（Billaudelle和Ahmad，2015）。