Model-Based Representation and Deinterleaving of Mixed Radar Pulse Sequences With Neural Machine Translation Network
MENGTAO ZHU
摘要
混合雷达脉冲序列解交织是现代电子侦察系统截获并分析非合作雷达意图的首要且至关重要的步骤。当前,随着雷达调制复杂性的不断提升,这些系统正面临巨大挑战。本文提出一种基于每个源(分量脉冲序列)时间序列特征的混合雷达脉冲序列解交织新方法。首先,建立数学表示以描述每个源的结构特征;然后,将解交织问题转化为最大似然代价函数的最小化问题,该问题可通过监督式神经机器翻译(NMT)网络高效求解,即把交织脉冲序列中的每个接收脉冲映射到对应的源标签。本文提出序列到序列(seq2seq)NMT模型,以捕捉混合序列中来自同一源的非相邻脉冲间的结构关系,并为每个脉冲分配相应标签。所提方法无需知晓每个分量脉冲序列的精确信息。基于混合脉冲序列到达时间(TOA)序列的实验结果表明,该方法性能优于现有先进解交织方法,且在存在测量噪声和脉冲丢失的高度非理想条件下仍能取得令人满意的性能。该方法可直接应用于其他涉及解交织问题和多变量输入场景的领域。
I. 引言
随着射频(RF)频谱范围内辐射源数量的增加,电磁环境变得愈发复杂[1],[2],现代电子侦察系统必须处理来自周围多个雷达辐射源的密集交织脉冲序列(IPS)。通常,脉冲描述字(PDW)序列被用作后续频谱感知处理的输入数据。因此,基于PDW的混合脉冲序列解交织是现代电子侦察系统不可或缺的基础步骤。
现代雷达(如多功能雷达(MFR)或认知雷达(CR)[3]-[8])能够通过动态选择或优化脉冲间和脉冲内调制参数,感知环境并自适应调整发射信号。传统解交织方法面临以下几方面的巨大挑战:1)工作模式的脉冲模式动态变化。与早期脉冲模式几乎固定的雷达相比,现代雷达的脉冲序列具有灵活复杂的脉冲间调制[1],[9];2)脉冲序列中的模式切换。现代雷达可在时间轴上调度多种工作模式,以最优执行更高层级的雷达任务目标[10]-[17],这进一步加剧了解交织问题的复杂性;3)多个同时工作的同类型雷达。由于PDW中的所有参数值相同,混合PDW序列中蕴含的脉冲重复间隔(PRI)信息成为区分各源脉冲的唯一可用线索。因此,亟需研究新的解交织方法。
早期研究仅利用PRI信息开展解交织方法研究[18]-[28]。其他研究类别则采用PDW中的更多脉冲参数(如RF、到达方向(DOA)和脉冲宽度(PW))进行脉冲聚类[29]-[31]。这些方法在具有简单脉冲间调制和固定模板的传统雷达中取得了令人满意的性能。然而,先进分量雷达(如MFR)更复杂的脉冲间调制以及频繁的模式切换,使得解交织任务变得更加困难。因此,应更加关注工作模式定义参数中蕴含的时间序列特征。
例如,RF参数可能具有滑动、抖动和参差等脉冲间调制;DOA参数包含基于雷达平台与拦截器之间运动学的轨迹信息。通过利用不同参数间的时间序列特征,可为传统解交织方法提供一种有益的替代或补充方案。
深度学习方法的最大优势之一是能够从原始数据中自动提取特征[32]-[37]。已有多种机器学习或深度学习方法被用于解交织任务[34]-[37]。文献[34]采用模糊自适应共振理论对脉冲重复频率进行聚类,以分离脉冲序列;文献[35]利用有限自动机实现在线解交织;文献[36]考虑采用循环神经网络表示复杂的时间序列特征,并递归解交织混合脉冲序列;文献[37]将解交织问题视为去噪问题,利用去噪自编码器(DAE)求解。文献[35]-[37]中的尝试优于传统解交织方法,尤其是在某些非理想场景下。然而,上述方法的有效性仅通过实验验证,无法确保其在现代先进雷达辐射源带来的广泛解交织挑战中仍能保持良好性能。为了更好地表示和理解解交织问题,并获得更具通用性和鲁棒性的解交织方案,需要解决分量脉冲序列、其交织过程以及解交织问题建模等问题。
在脉冲序列表示方面,现有研究大多侧重于通过基于模板的方式对单个雷达脉冲序列进行建模和表示。早期研究将辐射源参数化为固定参数[1],[38];随后,雷达字被用于描述具有特殊脉冲模式的脉冲多普勒(PD)雷达[3],[4],[39],但雷达字表示难以直接应用于其他雷达系统。之后,Ou提出雷达模式系统,包括雷达参数模式、脉冲模式和模式模式,与传统表示相比能更简洁地描述脉冲序列,其采用整个脉冲序列进行描述,并使用固定值(标量)、周期值(向量)和随机值(值区间)三种数据形式[40]。然而,这些方法仍基于模板,复杂且无法自适应现代雷达的特征;此外,上述基于模板的表示方法在描述自由度更高的认知雷达(CR)的动态特性时将失效。因此,在设计适用于现代雷达动态发射模式的新表示方法时,考虑雷达调制参数中的时间特征至关重要。
另一方面,利用时间序列特征的解交织方法为解决复杂脉冲序列解交织问题提供了可能,且处于持续发展中。其他领域的一些研究在对分量序列进行结构假设的前提下考虑了解交织问题[41]-[46]。这些研究将解交织问题分为分量序列、交织过程和解交织建模三部分,通常假设分量序列遵循某种概率模型,如高斯分布模型[42],[43]、马尔可夫链模型[44],[45]和隐马尔可夫模型(HMM)[41]。这些研究为解交织问题的建模和求解提供了严谨的探索和理解。最近,文献[46]考虑利用TOA数据对全高斯抖动分量雷达脉冲序列进行解交织,将解交织问题建模为最大似然(ML)问题,并在不同路径剪枝策略下用四种算法求解。文献[46]的研究从理论层面更好地理解了解交织任务和方法。然而,这些数学方法[41]-[46]在解决雷达解交织问题时存在以下主要局限性:1)存在测量噪声和脉冲丢失等非理想场景,上述数学模型仅考虑或可扩展到存在测量噪声的情况,面对脉冲丢失时,因模型失配可能导致性能严重下降;2)当所有模型未知时,一方面需要设计新的算法估计模型参数,再应用解交织算法,另一方面需通过穷举搜索求解ML问题,计算量大且耗时;3)当输入脉冲流包含不同结构配置的分量序列时,上述方法将面临巨大挑战;4)每个源的时间序列特征先验信息可能并非总能获得。尽管存在上述实际问题,但这些研究为基于分量脉冲序列时间序列特征的解交织过程数学分析提供了有前景的方向,且近期已有获取先验信息的尝试。例如,一个前置深度网络可获取IPS所需的先验信息[47],该网络接收IPS,输出每个源的PRI值以及PRI调制方式,其输出经进一步研究可作为基于时间序列的解交织方法所需的先验信息。
本文针对单个分量雷达脉冲序列和多个脉冲序列的交织过程,提出基于新时间序列表示的解交织任务数学建模方法。
首先,首次采用参数化概率模型描述脉冲序列。这一操作的合理性基于以下事实:雷达设计者和研究人员本身是概率论的熟练应用者,雷达系统中许多处理技术均源于概率论。例如,目标(接收回波)的特征[48]是通过概率方法建模和处理的。因此,对于截获工程师和研究人员而言,采用参数化概率模型描述雷达的行为特征(即接收脉冲序列)是直观且合理的。另一方面,所提基于模型的表示方法有效,可支持现代电子侦察系统的多项任务,包括解交织、辐射源类型识别、工作模式识别和数据库构建;此外,可从数学角度深入理解非合作雷达的行为特征,例如,变点检测理论[49]可用于在线多功能雷达工作模式切换检测;对于下一代雷达(CR),其特征也可通过概率图模型等概率模型[50]进行建模。
基于后续建立的多个脉冲序列混合的数学表示,本文借鉴文献[44]-[46]的研究,设计了一个统一的解交织框架,包含适用于不同实际场景的多种求解方案。在传统ML求解方案中,当分量序列的所有模型参数已知时,推荐使用基于动态规划的算法;当所有模型参数未知时,联合估计与解交织问题为NP难问题,需采用穷举搜索方法。特别地,本文重点研究受作者前期研究[51]启发的序列到序列(seq2seq)深度模型,提出seq2seq神经机器翻译(NMT)网络,以捕捉混合序列中来自同一源的非相邻脉冲间的时间序列关系,并为每个脉冲分配相应标签。
在两种分量序列先验信息假设下,基于标注TOA参数的混合脉冲序列进行了大量实验:1)所有分量序列已知;2)所有分量序列的参数在给定参数空间内随机生成。实验还验证了所提方法对多变量输入场景的适应性。实验结果表明,即使在存在测量噪声和脉冲丢失的高度非理想条件下,所提方法仍优于现有先进解交织方法。该方法可直接应用于其他涉及解交织问题的领域[52]-[54]。
本文的主要贡献如下:
1)分量脉冲序列及其混合过程的数学表示:首次设计分层定义和基于概率模型的表示方法,描述分量脉冲序列(雷达)的时间序列特征,该分层定义是对现有MFR分层模型[3],[55]中“符号到脉冲”层的完善补充。
2)基于分量脉冲序列表示定义多个分量序列的交织过程,并基于上述基于模型的序列表示建立脉冲序列解交织的数学建模。
3)包含两类解交织方案的基于模型的解交织处理框架:实现一种新的基于NMT的方法,与现有先进解交织方法相比,在多种实际场景下均能取得更优性能。
本文其余部分安排如下:第二节描述解交织问题的数学表示和建模;第三节介绍所提方法;第四节呈现实验设计和结果分析;最后,第五节总结全文。
II. 基于模型的表示与解交织问题建模
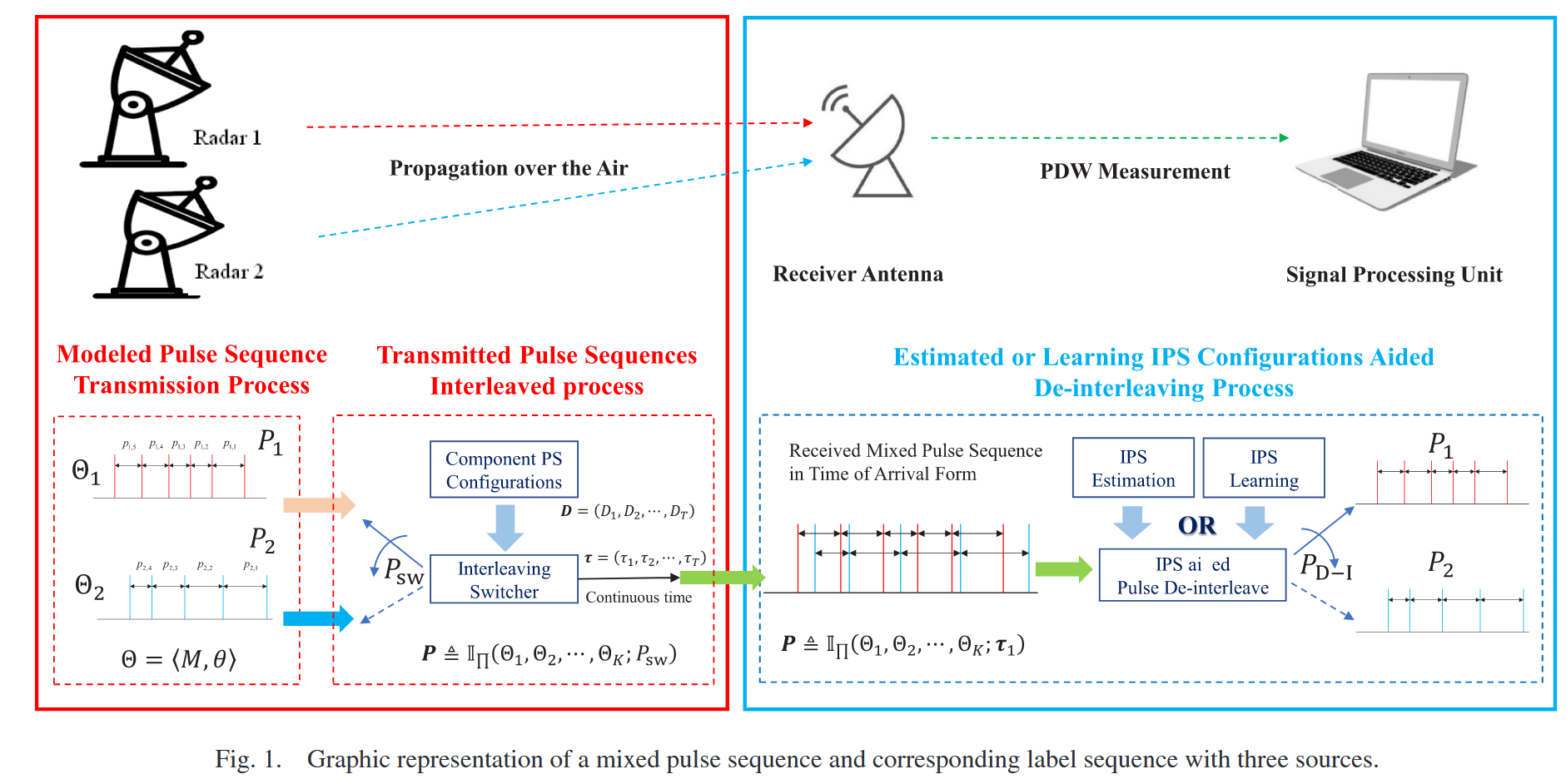
随着现代雷达的发展,用于实现系统功能的脉冲序列变得愈发复杂,具有动态变化的脉冲间调制和调制参数。本节从三个部分描述所提基于模型的表示与解交织问题建模。图1展示了含两个源的混合脉冲序列及其对应的标签序列。具体而言,第二节A描述MFR工作模式的分层定义及其在单PRI参数与IPS配置下的实现;第二节B和第二节C分别从数学角度设计交织过程、IPS以及相应的知识辅助解交织过程。
II.A 雷达脉冲序列的基于模型表示
1)MFR工作模式的分层定义
雷达脉冲序列的四个基本定义如下:
定义1 雷达工作模式是指为实现特定雷达功能而对有限个有序脉冲进行的专门排列。工作模式为P=(p1,p2,...,pL)∈RM×LP=(p_{1}, p_{2}, ..., p_{L}) \in \mathbb{R}^{M ×L}P=(p1,p2,...,pL)∈RM×L的雷达,需发射长度为L的脉冲序列以完成特定功能的工作模式。雷达脉冲p∈RMp \in \mathbb{R}^{M}p∈RM在工作模式P中由M个工作模式定义参数构成的实值向量表示为p=(p1,p2,...,pM)Tp=(p_{1}, p_{2}, ..., p_{M})^{T}p=(p1,p2,...,pM)T。
注:为避免问题进一步复杂化,假设混合脉冲序列中每个源的脉冲序列仅包含单一工作模式,即无模式切换。这意味着本研究中雷达的时间序列特征与给定发射工作模式的时间序列特征一致。
定义2 工作模式定义参数用于描述雷达工作模式的某一特征。从雷达角度看,工作模式定义参数通常指为执行不同雷达功能而优化的控制参数;从非合作接收方角度看,工作模式定义参数通常指PDW格式中用于描述工作模式的相关参数,如PRI、RF、PW和调制方式(MOP)。
定义3 参数调制类型是指给定工作模式下某一工作模式定义参数的脉冲间调制模式。不同参数适用的调制类型可能不同。六种常用的PRI调制类型包括恒定PRI、抖动PRI、驻留切换PRI、参差PRI、滑动PRI和正弦PRI[1],[9]。
定义4 调制定义参数是指定义某一工作模式定义参数的参数调制类型的特定调制参数。例如,均值和方差是高斯抖动参数调制类型的两个基本调制定义参数。

图2展示了一个基于多变量PDW序列定义的雷达工作模式示例。图中,vk=vk1,vk2,...,vkMkv_{k}={v_{k}^{1}, v_{k}^{2}, ..., v_{k}^{M_{k}}}vk=vk1,vk2,...,vkMk表示第k个工作模式定义参数的调制类型,MkM_{k}Mk为调制类型总数;对于第l种调制类型vklv_{k}^{l}vkl(1≤l≤Mk1 ≤l ≤M_{k}1≤l≤Mk),pkl=pkl,1,pkl,2,...,pkl,Nlp_{k}^{l}={p_{k}^{l, 1}, p_{k}^{l, 2}, ..., p_{k}^{l, N_{l}}}pkl=pkl,1,pkl,2,...,pkl,Nl表示调制定义参数,NlN_{l}Nl为调制定义参数总数。
以图2为例,存在M个考虑的工作模式定义参数,PRI为第一个工作模式定义参数(即k=1k=1k=1);图2(b)中考虑四种PRI调制类型:恒定、参差、抖动、滑动,其中参差是PRI调制的第二种类型(即l=2l=2l=2)。本文通过三个调制定义参数(如参差位置数、最小参差值和最大参差值)区分参差调制。图2(c)用于说明两个具有不同调制定义参数的参差示例的调制特征。
注:此处的分层定义与现有MFR分层模型(如文献[3]和[55]中的模型)不同。这些研究侧重于自上而下地建模雷达行为,包含任务层、命令层和字层等多个抽象功能层;基于雷达资源管理器的特征,通过从高层(雷达任务)到低层(雷达作业)的指令信息分配实现分层模型。然而,这两项研究中最低“符号表示层”(本研究中的工作模式、文献[3]中的雷达字、文献[55]中的雷达字母或音节)的可执行脉冲排列仅包含固定的脉冲间调制。为提升其方法对先进雷达带来的巨大挑战的建模能力,需在“符号到脉冲”层提供更复杂的调制。上述分层定义可视为对现有MFR分层模型“符号到脉冲”层的完善补充。
接下来,从概率角度呈现每个源时间序列特征的两级表示。
2)MFR工作模式的两级表示
PRI是PDW中最重要的参数,因其具有固有的时间特征,且截获的交织脉冲流在很大程度上受每个分量雷达的PRI特征影响。因此,为简化问题,仅考虑PRI工作模式定义参数,单个雷达的工作模式可描述为二元组Θ=<M,θ>\Theta=< M, \theta>Θ=<M,θ>。M∈MM \in \mathbb{M}M∈M表示PRI调制类型,M\mathbb{M}M为该工作模式的调制类型空间;θ∈Ω\theta \in \Omegaθ∈Ω为相应的调制参数,Ω\OmegaΩ为M的调制参数空间,包含所有参数调制类型的调制定义参数的类型空间Ωtype\Omega_{type }Ωtype和值空间Ωvalue\Omega_{value }Ωvalue两个子空间。例如,M={抖动,滑动}M = \{抖动, 滑动\}M={抖动,滑动}表示工作模式具有高斯抖动和滑动两种可能的调制类型;当M=抖动M = 抖动M=抖动时,Ωtype=(μ,σ2)\Omega_{type}=(\mu, \sigma^{2})Ωtype=(μ,σ2)表示抖动调制参数为均值μ\muμ和方差σ2\sigma^{2}σ2;当M=滑动M = 滑动M=滑动时,Ωtype=(α,σ2)\Omega_{type}=(\alpha, \sigma^{2})Ωtype=(α,σ2),其中α\alphaα为滑动步长,σ2\sigma^{2}σ2为表示测量噪声的零均值高斯噪声方差。每个调制定义参数有其自身的参数值空间Ωvalue\Omega_{value }Ωvalue,例如μ∈(10,1000)μs\mu \in(10,1000) \mu sμ∈(10,1000)μs表示雷达可从(10,1000)微秒范围内选择抖动均值。因此,两级表示可细致描述MFR或CR等先进雷达灵活调整发射脉冲序列以实现优化工作模式的能力。
雷达工作模式可在粗粒度层面(采用预计算的调制类型和模板调制定义参数)或细粒度层面(采用调制类型和优化的调制定义参数)实现[3],[10],[56]。因此,可为每个MFR工作模式定义两级表示:
-
调制类型层面的工作模式(调制层面):调制类型层面的工作模式体现MFR或CR等先进雷达在相应空间内灵活调整发射参数调制类型和调制定义参数的能力。单个工作模式定义参数从调制空间M\mathbb{M}M中选取的调制M是一个概率分布族,对应调制参数空间Ω\OmegaΩ。如前所述,Ω\OmegaΩ包含类型空间Ωtype\Omega_{type }Ωtype和值空间Ωvalue\Omega_{value }Ωvalue。通常,M\mathbb{M}M和Ωtype\Omega_{type }Ωtype为具有固定分量的离散空间;对于早期基于模板的雷达,Ωvalue\Omega_{value }Ωvalue为离散空间,对于先进雷达则为连续空间。早期雷达可从预存储模板中选择调制定义参数值,此时预存储模板即为该调制的离散空间(例如,著名的Mercury PD雷达[3]的调制参数空间包含9个具有驻留切换调制类型的雷达字);先进雷达或CR[57]-[59]可在连续范围内优化调制定义参数,此时该连续范围即为调制类型的连续参数空间(例如,上述示例中雷达可从(10,1000)微秒的连续范围选择抖动均值)。
-
调制参数层面的工作模式(参数层面):这是工作模式的细粒度表示,可视为由相应调制类型控制的分布族中,具有固定调制定义参数的具体单个分布。例如,θ=(50,12)\theta=(50,1^{2})θ=(50,12)的PRI高斯抖动调制描述了由高斯抖动PRI及其对应的Ω\OmegaΩ定义的工作模式的参数层面工作模式。参数层面可视为调制层面工作模式的实例化或实现;具体而言,由于CR可在连续范围内优化调制定义参数,每个最终优化结果均可视为一个参数层面工作模式。
由于MFR工作模式通常由多个工作模式定义参数共同定义,此处简要讨论两级表示向多变量情况的扩展。假设不同工作模式定义参数相互独立,M\mathbb{M}M和Ω\OmegaΩ为所有工作模式定义参数的乘积空间,则工作模式的参数模型可通过各变量概率密度函数(PDF)的乘积直接扩展。例如,假设存在MvM_{v}Mv个独立变量,对应PDF分别为p1(X1n),p2(X1n),...,pMv(X1n)p_{1}(X_{1}^{n}), p_{2}(X_{1}^{n}), ..., p_{M_{v}}(X_{1}^{n})p1(X1n),p2(X1n),...,pMv(X1n)(其中X1n=(X1,X2,...,Xn)X_{1}^{n}=(X_{1}, X_{2}, ..., X_{n})X1n=(X1,X2,...,Xn)表示长度为n的脉冲序列),则其联合PDF表示为:
PMv(X1n)=∏m=1Mvpm(X1n)P_{M_{v}}\left(X_{1}^{n}\right)=\prod_{m=1}^{M_{v}} p_{m}\left(X_{1}^{n}\right)PMv(X1n)=m=1∏Mvpm(X1n)
当不同变量相关时,也可基于分量分布和相关性推导其联合PDF。
3)PRI调制的数学模型
本文重点利用每个源不同工作模式定义参数的时间序列特征进行解交织。由于PRI数据是固有的时序数据,利用PRI时间序列特征进行解交织比利用RF等其他参数更复杂。因此,本文仅基于PRI参数定义工作模式,并阐述方法和实验。本节介绍四种常用的PRI调制类型:高斯抖动PRI、滑动PRI、参差PRI和正弦PRI。文献[60]已为这四种调制建立了统计模型,其参数模型如下:
a)高斯抖动PRI:该调制使PRI围绕均值μ\muμ和方差σ2\sigma^{2}σ2的高斯分布抖动。由于脉冲序列的所有PRI值ptp_{t}pt均为正值,因此该分布为在p=0p=0p=0处截断的高斯分布。高斯抖动PRI的PDF定义为:
f(pt)=1Φ(μσ)2πσ2exp(−(pt−μ)22σ2)f\left(p_{t}\right)=\frac{1}{\Phi\left(\frac{\mu}{\sigma}\right) \sqrt{2 \pi \sigma^{2}}} \exp \left(-\frac{\left(p_{t}-\mu\right)^{2}}{2 \sigma^{2}}\right)f(pt)=Φ(σμ)2πσ21exp(−2σ2(pt−μ)2)
其中Φ\PhiΦ为标准正态累积分布函数。在雷达应用中描述PRI值时,当μ≫0\mu \gg 0μ≫0且μ≫σ\mu \gg \sigmaμ≫σ时,Φ(μσ)≈1\Phi(\frac{\mu}{\sigma}) \approx1Φ(σμ)≈1,因此Φ(μσ)\Phi(\frac{\mu}{\sigma})Φ(σμ)可忽略。
b)滑动PRI:考虑具有正步长的滑动PRI(即递增滑动PRI),其他滑动调制(包括递减滑动和三角滑动)可通过对递增滑动PRI进行变换得到。在一个滑动周期内,脉冲序列可表示为迭代形式:
pt=α+pt−1+ωtp_{t}=\alpha+p_{t-1}+\omega_{t}pt=α+pt−1+ωt
其中α>0\alpha>0α>0为滑动步长,ωt∼N(0,σ2)\omega_{t} \sim N(0, \sigma^{2})ωt∼N(0,σ2)为零均值、方差为σ2\sigma^{2}σ2的高斯噪声。
c)参差PRI:雷达切换一组离散且周期性排列的PRI值,形成参差PRI。雷达系统内部可通过离散马尔可夫模型描述参差PRI值的转换。从接收方角度看,由于可能存在测量噪声,有限观测矩阵无法描述截获的脉冲值,因此需将接收的参差PRI建模为高斯发射的隐马尔可夫模型(高斯HMM)。
高斯HMM可表示为三元组:
Θ=<A,B,π>\Theta=<A, B, \pi>Θ=<A,B,π>
其中A=[aij]M×MA=[a_{i j}]_{M ×M}A=[aij]M×M为M个状态的状态转移矩阵,π=(π1,π2,...,πM)\pi=(\pi_{1}, \pi_{2}, ..., \pi_{M})π=(π1,π2,...,πM)为初始状态分布,Q=(q1,q2,...,qM)Q=(q_{1}, q_{2}, ..., q_{M})Q=(q1,q2,...,qM)为高斯HMM的状态集。每个状态对应一个均值为μm\mu_{m}μm、方差为σm2\sigma_{m}^{2}σm2的高斯模型,这些高斯模型表示为B=(φ1,φ2,...,φM)B=(\varphi_{1}, \varphi_{2}, ..., \varphi_{M})B=(φ1,φ2,...,φM),φm\varphi_{m}φm的PDF定义为:
fφm(pt)=12πσm2exp(−(pt−μm)22σm2),1≤m≤Mf_{\varphi_{m}}\left(p_{t}\right)=\frac{1}{\sqrt{2 \pi \sigma_{m}^{2}}} \exp \left(-\frac{\left(p_{t}-\mu_{m}\right)^{2}}{2 \sigma_{m}^{2}}\right), 1 \leq m \leq Mfφm(pt)=2πσm21exp(−2σm2(pt−μm)2),1≤m≤M
这些状态对应每个参差位置的PRI值。
d)正弦PRI:正弦PRI表示为:
pt=Asin(2πft+ϕ)+c+ωtp_{t}=A \sin (2 \pi f t+\phi)+c+\omega_{t}pt=Asin(2πft+ϕ)+c+ωt
其中f=fcfsf=\frac{f_{c}}{f_{s}}f=fsfc,A为振幅,c为常数项,ϕ\phiϕ为相位。雷达选择调制载波频率fcf_{c}fc和相应的采样频率fsf_{s}fs生成正弦PRI序列;然而,从接收方角度看,雷达选择的fsf_{s}fs未知,因此将fcf_{c}fc和fsf_{s}fs共同建模为f。此外,为满足PRI的正值要求,需c>Ac>Ac>A。
随着先进雷达的发展,已有研究提出基于模型的数据库设计,用于存储MFR各分层的模型信息[3](例如,含9个雷达字的Mercury PD雷达,每个雷达字描述为脉冲模板并存储在数据库中)。未来,检索和存储非合作雷达的参数调制类型和调制定义参数等更多基于模型的信息是可能且必要的。此外,从雷达角度看,其通过基于模型的描述来刻画目标或杂波特征[48];因此,电子接收方采用基于模型的方式描述雷达行为是直观且合理的。
注:上述四种调制中的时间戳t均为离散时间。
II.B 交织过程的表示
本文考虑含K个源的混合脉冲序列,每个源PkP_{k}Pk的脉冲序列可通过参数模型Θk\Theta_{k}Θk描述。每个雷达在时间τk,i\tau_{k, i}τk,i发射一个脉冲(其中1≤i≤Nk1 ≤i ≤N_{k}1≤i≤Nk为脉冲索引,NkN_{k}Nk为第k个雷达的发射脉冲总数)。因此,IPS中每个源的第一个脉冲的TOA记为τk,1\tau_{k, 1}τk,1,该时间也称为第k个雷达的初始相位。
基于上述定义,交织过程是指从K个候选分量序列{Pk}\{P_{k}\}{Pk}(k=1,2,...,Kk=1,2, ..., Kk=1,2,...,K)生成P=(τ1,τ2,...,τT)∈R1×TP=(\tau_{1}, \tau_{2}, ..., \tau_{T}) \in \mathbb{R}^{1 ×T}P=(τ1,τ2,...,τT)∈R1×T的过程。直观上,可通过名为交织切换器PSWP_{SW}PSW的专用控制单元描述切换过程:切换过程控制一个在源标签集合Π={1,...,K}\Pi=\{1, ..., K\}Π={1,...,K}上的“令牌”,在不同源之间切换。通常,假设切换过程PSWP_{SW}PSW是状态为Π={1,...,K}\Pi=\{1, ..., K\}Π={1,...,K}的马尔可夫过程,具有初始状态概率π=(π1,π2,...,πM)\pi=(\pi_{1}, \pi_{2}, ..., \pi_{M})π=(π1,π2,...,πM)和转移概率A=[aij]A=[a_{i j}]A=[aij]。令Dt∈ΠD_{t} \in \PiDt∈Π表示PSWP_{SW}PSW在时间t的状态随机变量,则DtD_{t}Dt决定时间t的活跃源。交织过程P≜IΠ(P1,P2,...,PK;PSW)P \triangleq \mathbb{I}_{\Pi}(P_{1}, P_{2}, ..., P_{K} ; P_{SW})P≜IΠ(P1,P2,...,PK;PSW)的生成方式如下:切换过程PSWP_{SW}PSW以概率P(Dt=j∣Dt−1=i)=aijP(D_{t}=j | D_{t-1}=i)=a_{i j}P(Dt=j∣Dt−1=i)=aij决定时间t的活跃源;活跃源PkP_{k}Pk在时间t发射一个新脉冲,并根据Θk\Theta_{k}Θk输出观测值τt\tau_{t}τt,其他源保持空闲。例如,若PkP_{k}Pk在时间t和t+Tt+Tt+T活跃,则无论间隔时间τt+T−τt\tau_{t+T}-\tau_{t}τt+T−τt长短,P中时间t和t+Tt+Tt+T的脉冲均为PkP_{k}Pk的连续脉冲。
通常,假设分量过程遵循相同的概率分布,且切换过程与分量过程独立[41]-[46]。然而,在雷达应用中,分量过程的一阶差分(每个源的TOA序列)服从某种概率分布,并由参数模型Θk\Theta_{k}Θk控制;交织过程P中各分量过程的服从分布可能不同,且切换过程与分量过程相关。具体而言,Π={1,...,K}\Pi=\{1, ..., K\}Π={1,...,K}为K个候选源标签,PSWP_{SW}PSW的初始状态概率由每个源的初始相位τk,1\tau_{k, 1}τk,1决定,转移概率依赖于PkP_{k}Pk,即通过对所有源的TOA τk,i\tau_{k, i}τk,i按升序排序得到DtD_{t}Dt;时间间隔τt+T−τt\tau_{t+T}-\tau_{t}τt+T−τt为源PkP_{k}Pk的PRI值,所有PRI值及其时间序列特征由Θk\Theta_{k}Θk控制。因此,交织过程P≜IΠ(P1,P2,...,PK;PSW)P \triangleq \mathbb{I}_{\Pi}(P_{1}, P_{2}, ..., P_{K} ; P_{SW})P≜IΠ(P1,P2,...,PK;PSW)可修正为P≜IΠ(Θ1,Θ2,...,ΘK;τ1)P \triangleq \mathbb{I}_{\Pi}(\Theta_{1}, \Theta_{2}, ..., \Theta_{K} ; \tau_{1})P≜IΠ(Θ1,Θ2,...,ΘK;τ1),其中τ1=τ1,1,τ2,1,...,τK,1\tau_{1}={\tau_{1,1}, \tau_{2,1}, ..., \tau_{K, 1}}τ1=τ1,1,τ2,1,...,τK,1为每个分量源的初始相位。
雷达应用中的交织过程P记为IPS,P≜IΠ(Θ1,Θ2,...,ΘK;τ1)P \triangleq \mathbb{I}_{\Pi}(\Theta_{1}, \Theta_{2}, ..., \Theta_{K} ; \tau_{1})P≜IΠ(Θ1,Θ2,...,ΘK;τ1)记为P的IPS配置。注:IPS配置中不包含每个源的消失时间,因为所提模型可通过将给定序列分割为多个连续的IPS配置来表示源消失的情况。例如,当含K个源的IPS配置P中第k个源在时间τendk\tau_{end }^{k}τendk消失时,将产生两个新的IPS配置:第一个包含K个源,终止于τendk\tau_{end }^{k}τendk;第二个起始于τ>τendk\tau>\tau_{end }^{k}τ>τendk的下一个脉冲,包含剩余K−1K-1K−1个源。下一节将基于IPS的描述讨论解交织问题的建模。
II.C 解交织问题的数学建模
1)解交织问题的统一建模
解交织算法的目标是基于τk,i\tau_{k, i}τk,i的时间序列特征,为IPS P中的每个脉冲分配源标签DtD_{t}Dt。所提算法不仅限于基于τk,i\tau_{k, i}τk,i实现,还可直接扩展到多变量情况。假设每个源的PRI服从某一已知参数分布(参数空间已知),但确切参数可能已知或未知。该假设基于以下两点考虑:一是雷达可能的PRI调制类型通常可提前知晓;二是参数空间受雷达的功能用途或工程实现约束。
接收的混合脉冲序列记为P=(τ1,τ2,...,τT)∈R1×TP=(\tau_{1}, \tau_{2}, ..., \tau_{T}) \in \mathbb{R}^{1 ×T}P=(τ1,τ2,...,τT)∈R1×T(其中τt\tau_{t}τt为第t个脉冲的TOA),也可表示为分量形式P=(P1,P2,...,PK)P=(P_{1}, P_{2}, ..., P_{K})P=(P1,P2,...,PK)(其中Pk=τk,iP_{k}=\tau_{k, i}Pk=τk,i,1≤i≤Nk1 ≤i ≤N_{k}1≤i≤Nk)。PkP_{k}Pk为P中第k个雷达的有序脉冲,其一级差分可通过参数模型Θk\Theta_{k}Θk建模。因此,含K个雷达的给定脉冲序列P可表示为参数模型形式P=<Θ,D>P=<\Theta, D>P=<Θ,D>,其中Θ=Θ1,Θ2,...,ΘK\Theta={\Theta_{1}, \Theta_{2}, ..., \Theta_{K}}Θ=Θ1,Θ2,...,ΘK为P的参数模型全集,Θk\Theta_{k}Θk为第k个雷达的参数模型;相应的标签序列记为D=(D1,D2,...,DT)D=(D_{1}, D_{2}, ..., D_{T})D=(D1,D2,...,DT)(其中Dt∈{1,...,K}D_{t} \in\{1, ..., K\}Dt∈{1,...,K},1≤t≤T1 ≤t ≤T1≤t≤T为P中第t个脉冲的雷达标签),也可表示为分量形式D=D1,D2,...,DKD={D^{1}, D^{2}, ..., D^{K}}D=D1,D2,...,DK(其中DkD^{k}Dk表示P中第k个雷达的脉冲分配,即第k个雷达生成的脉冲索引)。相应地,PkP_{k}Pk表示第k个雷达生成的脉冲。例如,若标签序列为D=(1,2,1,2,1,2)D=(1,2,1,2,1,2)D=(1,2,1,2,1,2),则D1=(1,3,5)D^{1}=(1,3,5)D1=(1,3,5),D2=(2,4,6)D^{2}=(2,4,6)D2=(2,4,6),P1P_{1}P1和P2P_{2}P2分别表示τD1\tau_{D^{1}}τD1和τD2\tau_{D^{2}}τD2。
通常,现有研究将解交织问题建模为最大似然(ML)代价函数的最小化问题,代价函数定义为:
L(P,Θ,D)=−ln[∏k=1K∏t∈Dkl(τt,Θk)]=−∑k=1K∑t∈Dklnl(τt,Θk)=−∑k=1KlnLk(τt,Dk,Θk)\begin{aligned} L(P, \Theta, D) & =-\ln \left[\prod_{k=1}^{K} \prod_{t \in D^{k}} l\left(\tau_{t}, \Theta_{k}\right)\right] \\ & =-\sum_{k=1}^{K} \sum_{t \in D^{k}} \ln l\left(\tau_{t}, \Theta_{k}\right) \\ & =-\sum_{k=1}^{K} \ln L^{k}\left(\tau_{t}, D^{k}, \Theta_{k}\right) \end{aligned}L(P,Θ,D)=−ln[k=1∏Kt∈Dk∏l(τt,Θk)]=−k=1∑Kt∈Dk∑lnl(τt,Θk)=−k=1∑KlnLk(τt,Dk,Θk)
其中l(τt,Θk)l(\tau_{t}, \Theta_{k})l(τt,Θk)为脉冲τt\tau_{t}τt在模型Θk\Theta_{k}Θk下的似然度,lnLk(τt,Dk,Θk)\ln L^{k}(\tau_{t}, D^{k}, \Theta_{k})lnLk(τt,Dk,Θk)为P中第k个源的对数似然度。对数似然函数的形式取决于第二节A3中描述的每个源的概率分布。以全高斯抖动调制为例,代价函数表示为:
L(P,Θ,D)=−∑k=1K∑tlnTk(τDk(t)−τDk(t−1))L(P, \Theta, D)=-\sum_{k=1}^{K} \sum_{t} \ln \mathscr{T}_{k}\left(\tau_{D^{k}(t)}-\tau_{D^{k}(t-1)}\right)L(P,Θ,D)=−k=1∑Kt∑lnTk(τDk(t)−τDk(t−1))
其中Tk\mathscr{T}_{k}Tk为第k个源的高斯PDF,Dk(t)D^{k}(t)Dk(t)表示分配给第k个源的第t个脉冲。
2)所提框架在不同场景的映射
尽管单个交织脉冲序列可由某一IPS配置描述,但考虑到脉冲序列可能的混合参数,实际解交织条件存在多种情况。例如,假设场景中雷达的最大数量为K,则处理过程中同时活跃的雷达数量k可在1到K之间变化,此时P可能存在∑k=1KCKk−1=2K−1\sum_{k=1}^{K} C_{K}^{k}-1=2^{K}-1∑k=1KCKk−1=2K−1种IPS配置(其中CKk=K!k!(K−k)!C_{K}^{k}=\frac{K !}{k !(K-k) !}CKk=k!(K−k)!K!为组合数)。本节从IPS配置角度将所提框架映射到五种典型场景,表1列出的五种典型场景几乎涵盖了雷达应用中所有可能的解交织场景。
表1 基于IPS配置定义的五种典型解交织场景
| 场景 | 描述 |
|---|---|
| 场景1 | 常规雷达或单功能雷达脉冲解交织。常规雷达参数固定;源数量K固定;每个源的模型Θk\Theta_{k}Θk为参数层面;每个源的初始相位随机分布。 |
| 场景2 | 无模式切换的MFR脉冲解交织。源数量K固定;每个源的模型Θk\Theta_{k}Θk为调制层面;每个源的初始相位随机分布。由于MFR包含多种工作模式,IPS配置中Θk\Theta_{k}Θk定义修正为Θk=Θk1,Θk2,...,Θklk\Theta_{k}={\Theta_{k}^{1}, \Theta_{k}^{2}, ..., \Theta_{k}^{l_{k}}}Θk=Θk1,Θk2,...,Θklk(其中Θkl\Theta_{k}^{l}Θkl(1≤l≤lk1 ≤l ≤l_{k}1≤l≤lk)为第l种工作模式,lkl_{k}lk为第k个MFR的工作模式总数)。 |
| 场景3 | 有模式切换的MFR脉冲解交织。源数量K固定;每个源的模型Θk\Theta_{k}Θk为调制层面;每个源的初始相位随机分布。场景2中Θk\Theta_{k}Θk定义修正为$\Theta_{k}={\Theta_{k}^{1}, \Theta_{k}^{2}, …, \Theta_{k}^{l_{k}} |
| 场景4 | 活跃MFR数量可变的解交织过程。场景中源的最大数量K已知,但活跃雷达数量未知且可变;每次所有活跃MFR发射单一工作模式,无模式切换。源数量k可变;每个源的模型Θk\Theta_{k}Θk为调制层面;每个源的初始相位随机分布。 |
| 场景5 | 模型相同雷达脉冲解交织。分量雷达的调制类型和调制参数相同;为基于IPS配置解交织相同雷达,这些雷达的初始相位需非重叠;源数量K固定;每个源的模型Θk\Theta_{k}Θk为参数层面;每个源的初始相位手动设置。 |
注:场景5中“相同”指雷达的发射波形、脉冲间调制和调制参数相同,不包含特定辐射源识别的“指纹”信息;本研究中用于解交织的发射PDW序列完全相同。
3)所提方法对其他类型雷达的适用性讨论
本研究的主要目标是给出考虑当前先进雷达复杂脉冲间调制的交织脉冲序列数学模型和表示方法,进而设计基于模型的交织脉冲序列解交织框架。以多功能雷达为例,基于PRI定义的工作模式阐述了时间序列特征。
基于接收方视角的雷达信号特征,通过相应修改,可将基于模型的表示扩展到其他类型雷达(及其他参数),进而对交织过程/序列和解交织问题进行建模,最终应用所提算法。例如,火控雷达通常工作在高信息率的固定模式,而非频繁模式切换的MFR,这类雷达可在场景1下以单功能雷达形式验证;对于有源天线应用,天线辐射模式产生的调制可能作用于脉冲幅度参数,该参数也可通过参数建模并补充到所提框架中。
III. 方法
III.A 解交织方案的示意图设计
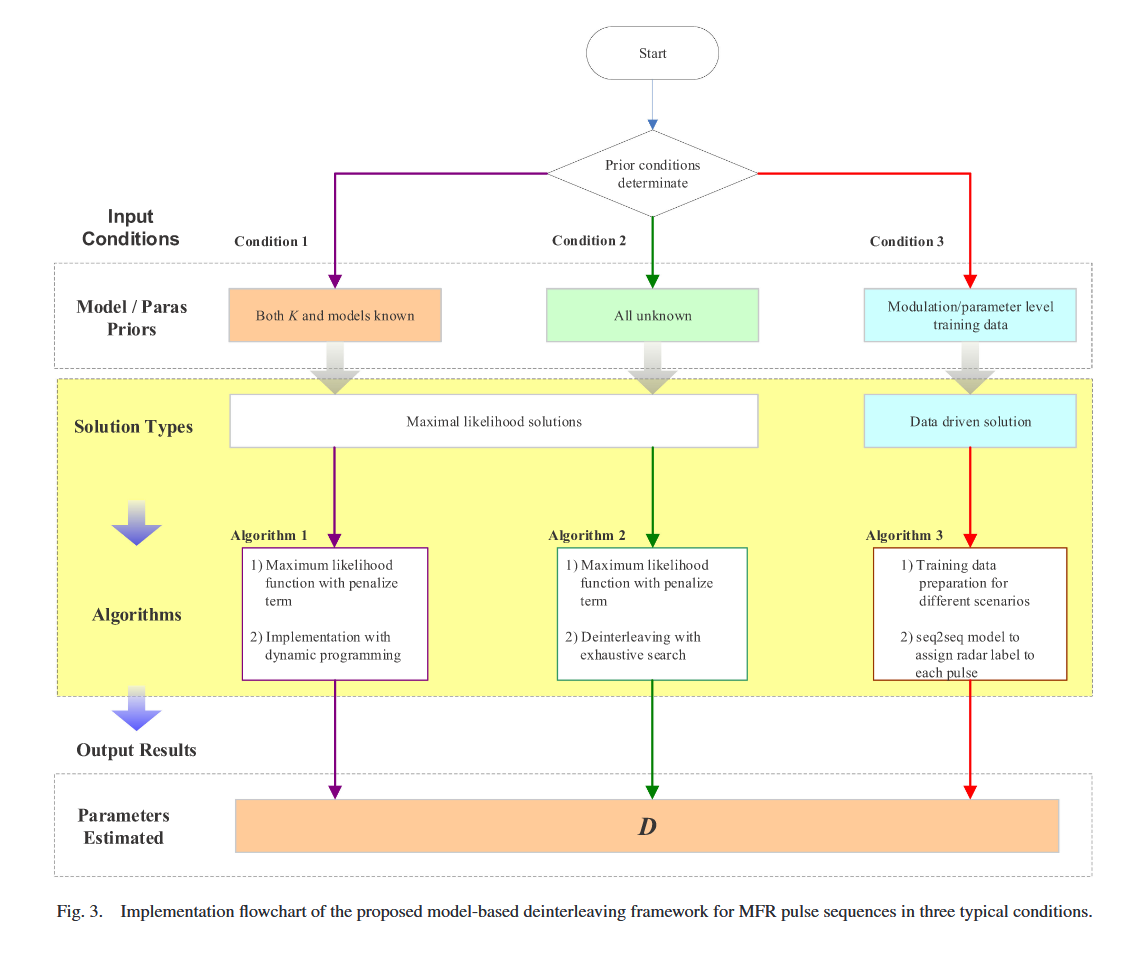
图3展示了所提基于模型的MFR脉冲序列解交织框架在三种典型条件下的整体实现流程图。解交织问题的求解方案主要分为两类:基于ML的求解方案和基于NMT的求解方案。两种方案的目标相同,即获取每个脉冲的真实雷达标签分配D=(D1,D2,...,DT)D=(D_{1}, D_{2}, ..., D_{T})D=(D1,D2,...,DT)。
基于分量源的不同先验假设,设计基于时间序列特征的解交织框架是合理的。流程图分为三条路径,对应图3描述的三种条件,每条路径均给出了先验信息、解交织算法和输出结果。算法1(A-1)和算法2(A-2)通过求解第二节C1中描述的ML代价函数解决解交织问题(A-1:minDL(P,Θ,D)min _{D} L(P, \Theta, D)minDL(P,Θ,D);A-2:minD,ΘL(P,Θ,D)min _{D, \Theta} L(P, \Theta, D)minD,ΘL(P,Θ,D)),可能采用惩罚项βklog(T)\beta k\log(T)βklog(T)(其中β\betaβ为非负常数,k为P的参数数量)。A-1在提前已知所有源模型的情况下,通过动态规划求解解交织问题;A-2需同时进行解交织和每个源的模型参数估计,属于组合优化和连续优化问题,为NP难问题。A-2需假设辐射源的最大可能数量K和已知候选调制类型数量NmN_{m}Nm,对于长度为T的交织序列,需围绕∑k=1K(Nm)kkT\sum_{k=1}^{K}(N_{m})^{k} k^{T}∑k=1K(Nm)kkT种可能组合进行穷举搜索,并通过赤池信息准则或贝叶斯信息准则评估组合。本研究中,A-2可作为在少量先验信息下,基于分量脉冲序列时间序列特征进行解交织的最终方案。
近期研究[45],[46]将解交织问题建模为ML问题,并提出多种算法求解。ML方案在雷达解交织应用中存在以下两个主要局限性:1)需设计合适的参数模型形式、相应的模型估计和推理方法,以适应雷达特定应用中的可能非理想条件,但基于鲁棒统计分析的发展现状,目前存在数学难点[61];2)基于P的不同IPS配置,存在多种场景,现有数学方法需对每种IPS配置进行严谨验证,过程极为复杂(例如,现有方法仅分析了已知高斯抖动模型数量的序列配置[46])。
因此,为克服这些局限性并提供简洁有效的方法,本文受自然语言处理领域NMT方法的启发,提出一种数据驱动框架(图3中算法3)。深度学习模型是高度非理想条件下优秀的分布学习器,已被引入解交织任务[36],[37],[47]。本文基于交织脉冲序列的数学建模和后续的解交织建模,构建深度学习模型,其目标是捕捉混合序列中来自同一源的非相邻脉冲间的结构关系,并为每个脉冲分配相应标签,这与基于时间序列特征的解交织建模本质一致。所提框架适用于多种实际场景,与现有先进解交织方法相比,可实现更优的解交织性能和扩展能力。
III.B 基于序列到序列学习的解交织方法
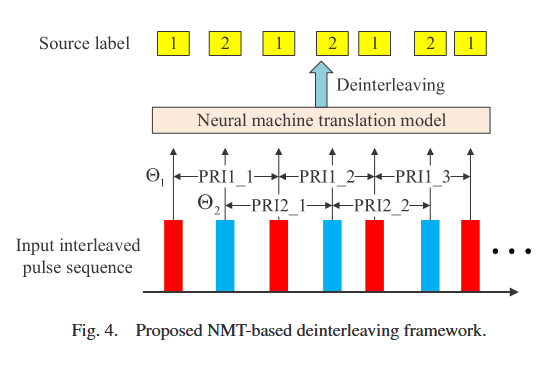
图4展示了利用NMT模型的处理框架。所提NMT框架采用序列到序列(seq2seq)学习结合长短期记忆网络(LSTM)实现。由于TOA序列P为非递减序列,不直接作为NMT模型的输入;相反,采用P的一阶差分P‾=(p1,p2,...,pT−1)\overline{P}=(p_{1}, p_{2}, ..., p_{T-1})P=(p1,p2,...,pT−1)作为输入,忽略P中最后一个脉冲的标签。基于NMT的解交织目标是为P‾\overline{P}P预测标签序列D^=(D^1,D^2,...,D^T−1)\hat{D}=(\hat{D}_{1}, \hat{D}_{2}, ..., \hat{D}_{T-1})D^=(D^1,D^2,...,D^T−1),即每个脉冲对应一个标签。
LSTM[62]及其变体[63],[64]已在包括脉冲序列分类[36]在内的多种应用中得到广泛研究。为捕捉混合序列中来自同一源的非相邻脉冲间的结构关系,并为每个脉冲分配相应标签,所提框架采用基于分层seq2seq的双向LSTM(bi-LSTM)网络。
训练数据集D=(P,D)\mathbb{D}=(P, D)D=(P,D)包含N个脉冲序列样本,其中P=(P‾1,P‾2,...,P‾N)P=(\overline{P}_{1}, \overline{P}_{2}, ..., \overline{P}_{N})P=(P1,P2,...,PN),D=(D1,D2,...,DN)D=(D_{1}, D_{2}, ..., D_{N})D=(D1,D2,...,DN),P‾i=(p1,p2,...,pT−1)\overline{P}_{i}=(p_{1}, p_{2}, ..., p_{T-1})Pi=(p1,p2,...,pT−1)为第i个样本。第一个bi-LSTM层分别从正向和反向迭代原始脉冲序列,生成隐藏状态向量Hf=(h1f,h2f,...,hT−1f)H^{f}=(h_{1}^{f}, h_{2}^{f}, ..., h_{T-1}^{f})Hf=(h1f,h2f,...,hT−1f)和Hb=(h1b,h2b,...,hT−1b)H^{b}=(h_{1}^{b}, h_{2}^{b}, ..., h_{T-1}^{b})Hb=(h1b,h2b,...,hT−1b):
htf=LSTM(pt,ht−1f),t=1,2,...,T−1h_{t}^{f}=LSTM\left(p_{t}, h_{t-1}^{f}\right), t=1,2, ..., T-1htf=LSTM(pt,ht−1f),t=1,2,...,T−1
htb=LSTM(pt,ht−1b),t=T−1,T−2,...,1h_{t}^{b}=LSTM\left(p_{t}, h_{t-1}^{b}\right), t=T-1, T-2, ..., 1htb=LSTM(pt,ht−1b),t=T−1,T−2,...,1
其中LSTM表示LSTM单元函数,由以下函数实现:
ft=σ(Wfpt+Rfht−1+bf)f_{t}=\sigma\left(W_{f} p_{t}+R_{f} h_{t-1}+b_{f}\right)ft=σ(Wfpt+Rfht−1+bf)
it=σ(Wipt+Riht−1+bi)i_{t}=\sigma\left(W_{i} p_{t}+R_{i} h_{t-1}+b_{i}\right)it=σ(Wipt+Riht−1+bi)
at=tanh(Wapt+Raht−1+ba)a_{t}=\tanh \left(W_{a} p_{t}+R_{a} h_{t-1}+b_{a}\right)at=tanh(Wapt+Raht−1+ba)
ot=σ(Wopt+Roht−1+bo)o_{t}=\sigma\left(W_{o} p_{t}+R_{o} h_{t-1}+b_{o}\right)ot=σ(Wopt+Roht−1+bo)
ct=ct−1×ft+at×itc_{t}=c_{t-1} \times f_{t}+a_{t} \times i_{t}ct=ct−1×ft+at×it
ht=tanh(ct)×oth_{t}=\tanh \left(c_{t}\right) \times o_{t}ht=tanh(ct)×ot
其中W和R分别表示输入权重和循环权重,b为偏置,ftf_{t}ft、iti_{t}it、oto_{t}ot和ata_{t}at分别表示遗忘门向量、输入门向量、输出门向量和输入向量,ctc_{t}ct为细胞状态。将HfH^{f}Hf和HbH^{b}Hb拼接(即H=[Hf;Hb]H=[H^{f} ; H^{b}]H=[Hf;Hb]),以汇总脉冲ptp_{t}pt周围整个脉冲序列的信息。
类似地,第二个bi-LSTM层对向量H进行计算,形成向量:
h~tf=LSTM(ht,h~t−1f),t=1,2,...,T−1\tilde{h}_{t}^{f}=LSTM\left(h_{t}, \tilde{h}_{t-1}^{f}\right), t=1,2, ..., T-1h~tf=LSTM(ht,h~t−1f),t=1,2,...,T−1
h~tb=LSTM(ht,h~t−1b),t=T−1,T−2,...,1\tilde{h}_{t}^{b}=LSTM\left(h_{t}, \tilde{h}_{t-1}^{b}\right), t=T-1, T-2, ..., 1h~tb=LSTM(ht,h~t−1b),t=T−1,T−2,...,1
同样,拼接H~f\tilde{H}^{f}H~f和H~b\tilde{H}^{b}H~b得到表示H~=[H~f;H~b]\tilde{H}=[\tilde{H}^{f} ; \tilde{H}^{b}]H~=[H~f;H~b]。
第二个bi-LSTM层生成输出向量序列A~=(a~1,a~2,...,a~T−1)\tilde{A}=(\tilde{a}_{1}, \tilde{a}_{2}, ..., \tilde{a}_{T-1})A~=(a~1,a~2,...,a~T−1),其中a~t\tilde{a}_{t}a~t表示为:
a~t=Wh~a~[h~tf⊕h~tb]+ba~\tilde{a}_{t}=W_{\tilde{h} \tilde{a}}\left[\tilde{h}_{t}^{f} \oplus \tilde{h}_{t}^{b}\right]+b_{\tilde{a}}a~t=Wh~a~[h~tf⊕h~tb]+ba~
其中⊕\oplus⊕表示向量拼接。
最后,将每个输出向量a~t\tilde{a}_{t}a~t输入softmax层,得到分类结果D^=(D^1,D^2,...,D^T−1)\hat{D}=(\hat{D}_{1}, \hat{D}_{2}, ..., \hat{D}_{T-1})D^=(D^1,D^2,...,D^T−1),其中D^t\hat{D}_{t}D^t为第t个脉冲所有源标签的输出概率分布。通过对P‾\overline{P}P中每个可能存在的源进行标签分类,并确定这些源的对应脉冲,完成解交织任务。
所提NMT模型中,网络对输入序列中每个脉冲的错误分类进行惩罚,训练目标是最小化N个训练序列样本的平均损失E‾\overline{E}E:
E‾=1N∑i=1N(−1Ti∑t=1TiDtlog(D^t))+λ2∥ω∥22\overline{E}=\frac{1}{N} \sum_{i=1}^{N}\left(-\frac{1}{T_{i}} \sum_{t=1}^{T_{i}} D_{t} \log \left(\hat{D}_{t}\right)\right)+\frac{\lambda}{2}\| \omega\| _{2}^{2}E=N1i=1∑N(−Ti1t=1∑TiDtlog(D^t))+2λ∥ω∥22
其中TiT_{i}Ti(i=1,2,...,Ni=1,2, ..., Ni=1,2,...,N)为第i个脉冲序列样本的脉冲数量,DtD_{t}Dt和D^t\hat{D}_{t}D^t分别为第t个脉冲的目标标签和对应分类输出,λ2∥ω∥22\frac{\lambda}{2}\|\omega\|_{2}^{2}2λ∥ω∥22为正则化项(用于减少过拟合,ω\omegaω为权重向量,λ\lambdaλ为正则化因子)。未来可探索更多新的seq2seq模型,以提升准确性和实时性能。
III.C 序列样本生成方法
基于P的IPS配置定义,可设计统一的数据准备流程。对于seq2seq学习框架,若测试阶段P的IPS配置数量存在变化,则需将所有可能的IPS配置拼接形成训练样本。拼接可使seq2seq学习器学习配置内和配置间的特征,进而适应测试样本中可变数量的IPS配置。第二节C2中描述的五种场景的具体实现细节见附录,以进一步说明数据准备流程。
IV. 实验
为验证所提解交织框架的有效性和优越性,基于模拟混合脉冲序列进行了全面实验。第四节A描述数据集、评价指标、基线方法和实验安排;第四节B至第四节D呈现并讨论实验结果。
IV.A 实验设计
1)数据集描述
本研究采用每个源的PRI数据进行解交织,通过五种PRI调制类型(高斯抖动、参差、滑动、正弦和恒定PRI调制)描述每个源的特征。根据第二节C2中描述的五种实际场景,生成五类数据集:
-
第一类数据集:常规雷达(参数固定)解交织。每个脉冲序列的模型参数完全已知,标签序列待估计;生成五个子数据集,分别对应五种调制组合(全高斯抖动、全参差、全滑动、全正弦、全恒定序列);混合脉冲序列的源数量K固定为3。
-
第二类数据集:无模式切换的MFR解交织。序列基于参数空间中随机采样的模型生成;测试阶段每个混合脉冲序列可视为未见过的序列,解交织过程采用粗粒度先验;生成五个子数据集,调制组合与第一类数据集相同。
-
第三类数据集:有模式切换的MFR解交织。根据附录C中描述的生成方法,生成两个可能的训练数据集;考虑两个MFR,每个包含三种调制层面定义的工作模式;测试数据集通过每个辐射源随机选择发射模式序列生成(即每个源的发射工作模式数量和类型随机选择,导致单个源脉冲序列的工作模式数量可变)。
-
第四类数据集:活跃雷达数量可变的解交织场景。假设活跃雷达的最大数量K=3K=3K=3,则存在23−1=72^{3}-1=723−1=7种IPS配置;训练数据集根据第三节C中描述的方法(附录D详细说明)生成;测试数据集生成三个子集(k=1,2,3k=1,2,3k=1,2,3),分别测试不同活跃雷达数量下的性能。
-
第五类数据集:模型相同雷达的解交织。由于仅采用PRI参数进行解交织,“相同”指分量雷达的PRI调制和调制参数完全相同,仅初始相位不同;采用两个具有高斯抖动PRI的相同雷达,基于参数层面设置进行交织。
注:实际电磁环境中,不同雷达的脉冲可能在时域重叠;当RF相同时,数字接收方难以分离无频率差异的重叠脉冲,可能将其视为一个整体,输出单个合并或受污染的PDW(例如,忽略后一个接收脉冲的TOA,导致另一个辐射源的后一个脉冲丢失;RF、PW、PA等参数可能测量错误)。由于本研究仅模拟不同分量雷达的PRI序列,因此将该问题表示为脉冲丢失的非理想条件(即后一个重叠脉冲的PRI无法被接收方测量和记录)。
调制层面设置中,每个源的初始PRI值和相应调制定义参数在给定范围内变化,不同调制定义参数的详细取值范围参考文献[9]的设置(表2);PRI值范围在对应章节说明(例如,不同源的滑动PRI序列在初始PRI值、滑动步数和滑动步长三个调制定义参数上变化,初始PRI值与不同源的PRI值范围相同)。
NMT模型包含两个bi-LSTM层,隐藏层大小分别为128和128,输出为序列;bi-LSTM层后为隐藏层大小500的全连接层;采用丢弃系数为0.25的dropout层避免过拟合[65]。
表2 调制层面设置的调制定义参数值空间
| 参数调制类型 | 调制定义参数 | 值空间 |
|---|---|---|
| 高斯抖动 | 均值 | 与不同源的PRI值范围相同 |
| 方差 | 所有源:[0,5][0,5][0,5] | |
| 正弦 | 平均PRI | 与不同源的PRI值范围相同 |
| 偏差 | 所有源:[10%,20%][10\%, 20\%][10%,20%] | |
| 滑动 | 滑动步长 | 所有源:[5,15][5,15][5,15] |
| 滑动步数 | 所有源:[4,8][4,8][4,8] | |
| 参差 | 参差位置数 | 所有源:[4,8][4,8][4,8] |
| 抖动 | 平均PRI | 与不同源的PRI值范围相同 |
| 偏差 | 所有源:[10%,15%][10\%, 15\%][10%,15%] |
2)基线方法
采用近期基于时间序列的解交织方法作为基线方法:
a)DPML:文献[46]中提出的基于动态规划的ML方法,用于高斯抖动雷达脉冲序列解交织;提出四种降低计算复杂度的解交织算法,以及一种模型参数未知时的源参数估计算法;仅考虑全高斯抖动调制的序列配置,忽略脉冲丢失条件的影响。
b)DAE:文献[37]中提出的基于去噪自编码器(DAE)的方法;将解交织问题建模为去噪任务,通过DAE实现。
3)性能评价指标
为便于比较和分析,解交织准确率定义如下:
acc=1N∑i=1N1Ti∑t=1TiI[D^t=Dt]acc=\frac{1}{N} \sum_{i=1}^{N} \frac{1}{T_{i}} \sum_{t=1}^{T_{i}} \mathbb{I}\left[\hat{D}_{t}=D_{t}\right]acc=N1i=1∑NTi1t=1∑TiI[D^t=Dt]
I[D^t=Dt]={1,若D^t=Dt0,其他情况\mathbb{I}\left[\hat{D}_{t}=D_{t}\right]= \begin{cases}1, & 若\hat{D}_{t}=D_{t} \\ 0, & 其他情况 \end{cases}I[D^t=Dt]={1,0,若D^t=Dt其他情况
其中N为测试样本数量,D^t\hat{D}_{t}D^t和DtD_{t}Dt分别为第t个脉冲的预测标签和对应源标签,TiT_{i}Ti为第i个测试样本的脉冲数量。
4)实验安排
基于五种场景和相应数据集,设计了一组验证和评估NMT解交织性能的实验:
a)所提方法的基本功能验证(第四节B):
- 不同源数量下的基本解交织能力;
- 非理想场景下的性能。
b)实际场景下的性能分析(第四节C):
- 有模式切换的MFR解交织;
- 活跃源数量可变的解交织;
- 模型相同雷达的解交织。
c)多变量场景的扩展性(第四节D)。

IV.B 所提方法的基本功能验证
本节从源数量增加和非理想场景两个方面验证所提解交织方法的基本功能。
1)不同源数量下的基本解交织能力
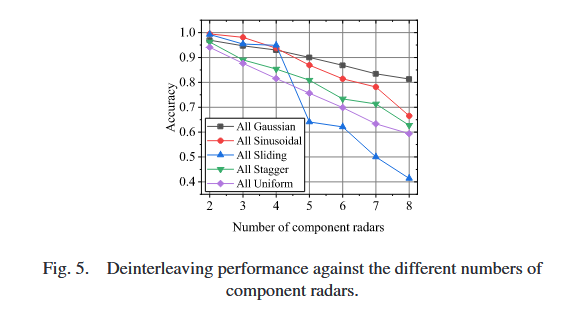
考虑参数层面和调制层面两种设置。基于分量源的不同组合,存在多种IPS配置;为简化,假设IPS中每个源服从相同分布。因此,分别采用全高斯抖动、全参差、全正弦、全滑动和全恒定五种调制场景,阐述解交织性能。源数量从2增加到8(步长为1),共7种源数量设置;IPS配置数量为5×7=355 ×7=355×7=35。由于IPS中所有源的调制类型相同,相应的调制参数或参数空间设置为不完全重叠;所有源的初始相位假设在同一时间间隔内均匀分布。每种K条件下的每个场景包含5000个IPS样本,按70%、15%、15%的比例分为训练集、验证集和测试集。为方便起见,八个雷达仅PRI值范围不同,其他调制参数范围相同:第一个雷达PRI值范围为[21, 40]μs,第二个为[41, 60]μs,第三个为[61, 80]μs,其余以此类推。测试集上不同雷达数量的解交织结果如图5所示。
实验结果表明,五种调制设置的性能随分量雷达数量增加而逐渐下降。对于调制层面设置,一方面解交织问题本身因雷达调制参数的变化而固有复杂;另一方面,随着分量雷达数量增加,性能自然下降;此外,由于PRI值范围为人工设置,雷达之间可能存在固有混淆[46]。
2)非理想场景下的性能
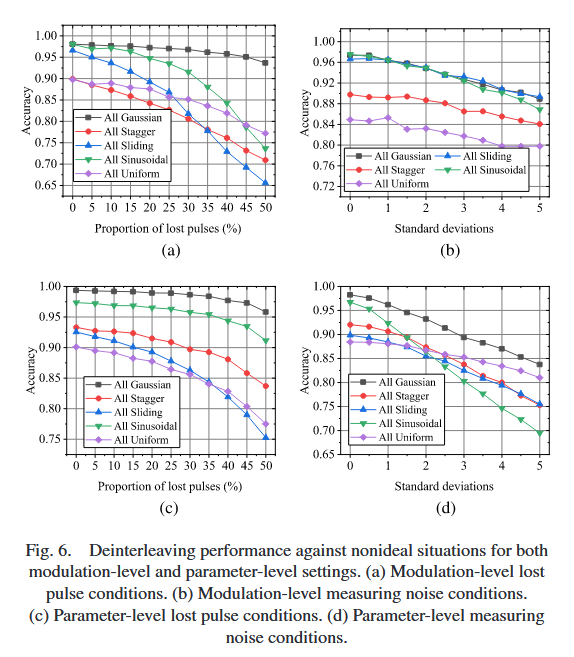
本节评估非理想场景(测量噪声和脉冲丢失)下的解交织性能。测量噪声假设为零均值、方差为σ2\sigma^{2}σ2的高斯分布,标准差(STD)从0增加到5μs(步长0.5μs),共11种噪声条件;脉冲丢失条件通过脉冲丢失率(LPR)描述,LPR从0增加到50%(步长5%),共11种脉冲丢失条件。每种非理想场景下,分别测试五种IPS配置(全高斯抖动、全参差、全正弦、全滑动、全恒定调制)。以测量噪声为例,每种噪声条件下的每个IPS配置包含2000个IPS样本,按70%、15%、15%的比例随机分为训练集、验证集和测试集;模型在所有噪声条件的训练集和验证集上训练,在每个噪声条件的测试集上单独测试,得到11个细粒度测试结果。
如图6所示,性能随场景恶化而下降;脉冲丢失条件对性能的影响大于测量噪声条件;全参差和全恒定调制的性能略低于其他三种场景;全高斯抖动调制受脉冲丢失和测量噪声条件的影响较小。对于调制层面设置的脉冲丢失条件,全高斯抖动的性能从LPR=0%时的98.07%下降到LPR=50%时的93.69%,而全滑动的性能从96.62%急剧下降到65.58%;参数层面设置的脉冲丢失条件下,性能下降比调制层面设置平缓。直观上,调制层面中seq2seq网络需要学习每个分量雷达的分布族,相比参数层面中学习每个分量雷达的精确分布更复杂。参数层面设置中,全高斯抖动和全滑动的性能分别从LPR=0%时的99.37%和92.55%下降到LPR=50%时的95.83%和75.26%。
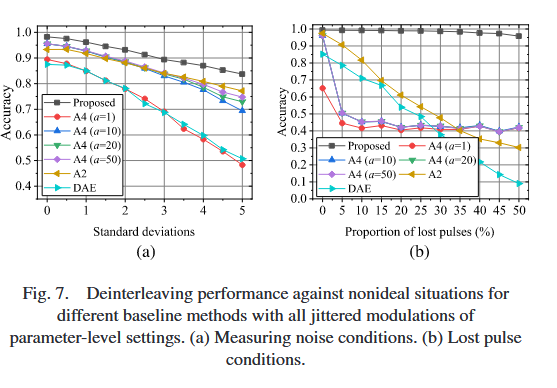
图7展示了参数层面设置下全高斯抖动调制的基线方法性能,每个源的详细调制定义参数遵循基线方法[46]的设置(三个源的均值分别为50、72、84,方差分别为0.820.8^{2}0.82、0.420.4^{2}0.42、0.040.040.04)。深度学习方法是高度非理想条件下优秀的分布学习器,图7表明所提方法在测量噪声和脉冲丢失条件下均显著优于其他基线方法。由于每个IPS样本中每个源的初始相位在[0, 50]μs范围内变化,基于连续时间的DAE方法性能下降;此外,基于全连接层的编码器-解码器方法无法提取时间序列特征[66],需通过位置编码[66]获得该能力;DPML中的A4算法可视为基于一阶马尔可夫假设(每个分量脉冲序列的时间序列特征)的维特比类算法,通过保留每一步的前a条最大似然路径作为下一步的初始路径,随着保留路径数量增加,性能逐渐提升,但仅利用TOA数据无法通过动态规划甚至穷举所有可能路径获得最优分配。基于DPML的方法在其参数模型中固有考虑了测量噪声,因此受测量噪声的影响较小;然而,脉冲丢失条件需要特殊设计的参数模型,因此相比测量噪声条件,性能显著下降。脉冲丢失会导致分量脉冲序列初始PRI的谐波,每个源对的最小公倍数较大,而这种大“PRI”(即TOA的一阶差分)需要多个连续脉冲丢失;由于本文采用均匀分布设置脉冲丢失,多个连续脉冲丢失的概率较低,从而降低了解交织任务的复杂度。实验结果表明,深度学习方法可从交织脉冲序列中学习含脉冲丢失的联合分布,准确率超过0.9。
图8展示了图7(a)中标准差为5时交织脉冲序列的详细结果:图8(a)为所提方法的测试样本解交织结果;图8(b)为所提方法和三种基线方法的错误预测情况。所提方法性能最优;对于基线方法,随着保留的最大似然路径数量减少(从A2到A4,a=20a=20a=20),性能总体下降。
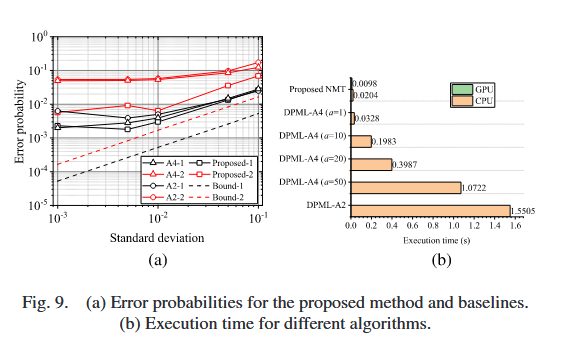
图9(a)比较了所提方法、A2和A4算法以及文献[46]中提出的交织高斯抖动脉冲序列的误差边界,两个交织源的均值分别为1和π,每个源的标准差从10−310^{-3}10−3增加到10−110^{-1}10−1;结果为每个源不同初始相位设置下200次试验的平均值(黑线表示源1,红线表示源2)。所提方法性能更优,更接近两个源的下界,尤其是源2;三种方法均表现出与误差边界相似的趋势;所有算法与下界之间存在差距,可能原因:1)下界为暴力计算边界,可能较宽松;2)三种算法实现了近最优结果。所提方法性能优于基线方法。基于时间序列特征的解交织方法的更多理论分析需要对每种IPS配置进行细致分析,将作为本文未来工作。
最后,比较算法复杂度。设脉冲数量为T,源数量为K:NMT网络和DPML-A4的时间复杂度为O(T)O(T)O(T);DPML-A2的近似复杂度为O(T(Mρ)K)O(T(\frac{M}{\rho})^{K})O(T(ρM)K)(其中M为源超时参数,ρ为平均脉冲间隔[46])。比较所提方法和DPML方法在参数层面设置(全高斯抖动调制)下的执行时间:DAE方法采用连续时间作为输入样本,与采用离散时间的DPML和所提方法不可直接比较;执行环境为Intel® Core ™ i9-10850H CPU和NVIDIA GeForce RTX 3080 GPU;记录所提方法在CPU和GPU上的执行时间;结果为5000个IPS样本(每个样本含200个脉冲)的平均值。图9(b)表明,所提方法在CPU设置下的执行时间低于A2和A4算法,且可在GPU平台进一步加速;A2算法保留所有无时间源超时的路径(细节见[46]),耗时最长;A4算法的执行时间随保留路径a的增加几乎线性增长。
调制层面设置下,DPML算法需额外步骤先估计每个抖动模型的PRI值(即其研究中的A5算法),再将估计参数代入模型;对于其他调制类型,目前尚无IPS中的估计方法;DAE方法无法处理调制层面设置,因为调制层面中每个源对应一个分布族,模型需更关注其时间序列特征。
IV.C 实际场景下的性能分析
第二节C2讨论了多种实际场景,解交织方法应在这些场景下表现出良好性能。本节考虑第二节C2中的场景3-5,由于现有基线方法未考虑这些场景,因此无法直接比较。
1)有模式切换的MFR解交织
有模式切换的MFR解交织给解交织方法带来巨大挑战,所提方法通过数据驱动方式解决该问题。本节考虑两个MFR,每个包含三种调制层面设置的不同工作模式(抖动、参差、滑动PRI);两个雷达的PRI范围分别为[51, 100]μs和[101, 150]μs。
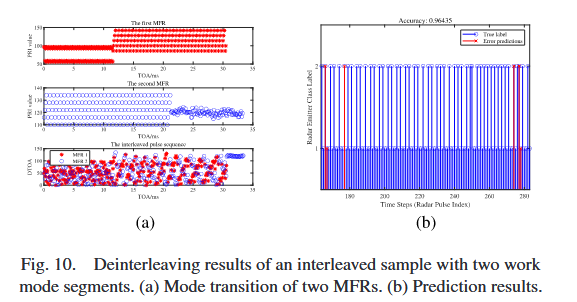
两个MFR可在发射脉冲序列中随机安排工作模式的类型和数量;采用附录C中提出的两种数据准备方法生成两类训练数据集;测试阶段,每个雷达可发射随机数量的工作模式类型,每种发射类型可调度可变数量的模式段(发射工作模式段数量从1到10,步长为1;每个段的发射脉冲数量在100到200之间手动变化,以进一步复杂化问题)。
实验结果表明,两种数据生成策略在测试数据集(含可变数量的发射工作模式段)上均能取得令人满意的性能;第二种策略的性能优于第一种策略:所有发射工作模式段数量下的解交织准确率超过98%,而第一种策略训练的模型准确率超过96%但低于97.5%。第二种策略直接拼接所有IPS配置,相比第一种策略可提供更细粒度、更高质量的训练数据。图10展示了含两个工作模式段的交织样本的解交织结果。
2)活跃源数量可变的解交织
动态环境中,存在的雷达最大数量可能固定,但每次当前活跃的雷达数量可变(第二节C2)。传统监督解交织方法难以处理该场景(类别数量变化),通常每种IPS配置需要一个指定模型;假设雷达最大数量为K,则需训练2K−12^{K}-12K−1个模型以适应该场景。然而,所提seq2seq框架中,单个训练模型可适应所有IPS配置;数据准备方法见附录D。测试阶段,活跃雷达数量从1增加到K,得到K个结果;每个雷达包含一个调制层面设置的单一工作模式。本节设计K=3的六种不同设置(表3)。
表3 K=3的六种设置
| 设置 | 雷达数量 | 调制类型 | PRI值范围 |
|---|---|---|---|
| 1 | 3 | 高斯、参差、滑动 | 均为U(51,100)U(51,100)U(51,100)μs |
| 2 | 3 | 全抖动 | 雷达1:U(51,100)U(51,100)U(51,100)μs;雷达2:U(101,150)U(101,150)U(101,150)μs;雷达3:U(151,200)U(151,200)U(151,200)μs |
| 3 | 3 | 全参差 | 同设置2 |
| 4 | 3 | 全滑动 | 同设置2 |
| 5 | 3 | 全正弦 | 同设置2 |
| 6 | 3 | 全恒定 | 同设置2 |
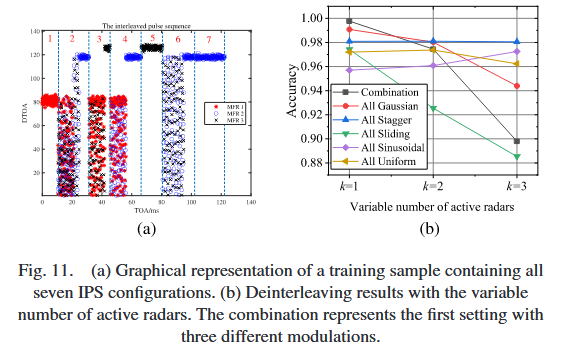
设置1中三个源的调制类型不同但PRI值范围相同,解交织需更多依赖PRI时间序列特征;其他五种设置中三个雷达的调制类型相同,因此相应的PRI值范围不重叠;每个源的相位在IPS样本中均匀分布于0到10μs之间。结果如图11(b)所示。
图11(a)展示了含所有7种IPS配置的训练样本(七种IPS配置用虚线分隔,上方标注红色数字)。通过拼接,NMT模型被迫学习配置间和配置内的特征,从而适应测试阶段可变数量的IPS配置。图11(b)表明,所有设置在所有k条件下的结果均超过88%;性能随k增加略有下降(直观上,活跃雷达数量越多,问题越复杂),但下降幅度平缓;例如,仅“组合”和“滑动”设置的性能下降较明显,其他四种设置的下降幅度较小。
3)模型相同雷达的解交织
环境中可能存在模型相同的雷达,基于本研究提出的IPS配置,两个相同雷达的唯一可区分特征是其初始相位。本节通过实验检验初始相位的影响。
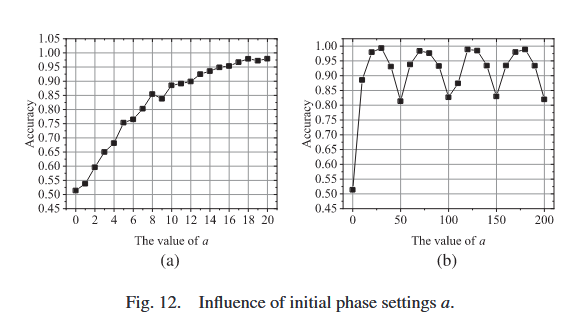
采用两个模型相同的雷达,发射抖动调制的脉冲序列(抖动调制的均值μ=50\mu=50μ=50,方差σ2=0.82\sigma^{2}=0.8^{2}σ2=0.82);第一个雷达的初始相位在[0, 10]μs范围内均匀分布;第二个雷达的初始相位范围从与第一个雷达完全重叠(即[0, 10]μs)逐渐远离(即范围为[a,a+10][a, a+10][a,a+10]μs,其中0≤a≤200 ≤a ≤200≤a≤20)。图12展示了初始相位设置的影响。
图12(a)表明,随着a值增加,两个模型相同雷达的初始相位距离逐渐增大,解交织性能提升;准确率从完全重叠(a=0a=0a=0)时的51.41%提升到远离(a=20a=20a=20)时的97.98%;当初始相位范围完全重叠时,监督分类器理论上无法区分它们。
由于PRI调制通常具有周期性,图12(b)展示了a取更大值时的影响。两个模型相同雷达的均值为50,因此性能在a为50的倍数(如a=50,100,150,200a=50,100,150,200a=50,100,150,200)时呈现周期性趋势。直观上,当第二个活跃雷达的初始相位接近第一个活跃雷达的第二个脉冲时,可能产生混淆;然而,与a=0a=0a=0时模型无法解交织两个雷达不同,这些情况下a为50的倍数时仅出现轻微性能下降。算法可基于第一个脉冲的PRI特征依次提取第一个雷达的脉冲,但当第二个雷达的初始相位接近第一个雷达第二个脉冲的TOA时,会产生混淆,这是性能下降的主要原因。
IV.D 多变量场景的扩展性
交织过程由每个源的PRI参数模型和初始相位控制;然而,每个雷达的PDW序列为多变量时间序列(如PRI、RF、PW)。此时,所提方法可直接应用于多变量场景(第二节A2)。本节通过PRI、RF和PW的不同调制组合人工定义三个雷达(表4)。
表4 三个人工定义的多变量雷达
| 雷达编号 | 工作模式定义参数 | 调制类型 | 均值范围 |
|---|---|---|---|
| 1 | PRI | 参差 | U(51,100)U(51,100)U(51,100)μs |
| RF | 高斯 | U(9000,9500)U(9000,9500)U(9000,9500)MHz | |
| PW | 恒定 | U(1,5)U(1,5)U(1,5)μs | |
| 2 | PRI | 参差 | U(101,150)U(101,150)U(101,150)μs |
| RF | 高斯 | U(9501,10000)U(9501,10000)U(9501,10000)MHz | |
| PW | 恒定 | U(6,10)U(6,10)U(6,10)μs | |
| 3 | PRI | 正弦 | U(51,100)U(51,100)U(51,100)μs |
| RF | 滑动 | U(9000,9500)U(9000,9500)U(9000,9500)MHz | |
| PW | 高斯 | U(1,5)U(1,5)U(1,5)μs |
设计中,雷达2的调制类型与雷达1相同,但均值范围不同;雷达3的均值范围与雷达1相同,但调制类型不同。最终解交织准确率为99.27%,性能优异。结果表明,所提方法可直接应用于多变量场景,只需对不同变量进行基本归一化以缓解不同变量量级差异的影响。而基于ML或DAE的方法则需要额外的算法操作才能适应多变量场景。
V. 结论
多功能雷达(MFR)或认知雷达(CR)等先进雷达能够感知环境并动态调整发射信号,因此其脉冲序列相比具有固定模板的传统雷达表现出显著的灵活性,这为这类复杂交织脉冲序列的解交织带来了巨大挑战。研究此类混合脉冲序列的解交织问题需涵盖两部分内容:分量源的表示方法,以及基于各源特征设计的解交织方法。
在表示层面,本文定义了雷达的四个基本概念——工作模式、工作模式定义参数、调制类型和调制定义参数,以全面描述先进雷达在脉冲模式上的动态特性与特征;随后,基于雷达的模型表示,从数学角度对交织过程进行建模;采用IPS配置完整描述交织脉冲序列的特征,并在IPS配置基础上提出解交织问题的统一建模方法,进而将该建模映射到五种典型的实际解交织场景。
在解交织方法层面,本文提出两种最大似然(ML)求解方案和一种数据驱动求解方案以解决解交织问题。基于神经机器翻译(NMT)的方法采用序列到序列(seq2seq)学习器实现;提出统一的数据准备方法用于训练NMT模型,并针对五种实际场景生成数据。通过考虑不同IPS配置两级设置的三类实验,评估了所提NMT方法的解交织性能与适应性。结果表明,该方法优于其他现有先进解交织方法,且能在基线方法无法处理的场景(如含模式切换的多功能雷达、活跃源数量可变等)中实现解交织。此外,该方法可直接扩展到多变量场景,且能应用于其他涉及解交织问题的领域。
利用时间序列特征对先进雷达脉冲序列进行解交织是一项艰巨的挑战,本研究是基于数据驱动方式的初步尝试。未来仍有多个方向需进一步研究:首先,需对IPS配置的唯一性进行数学分析,以严谨地剖析解交织问题;其次,需设计所需先验信息更少的数学方法,因为实际电磁环境中可能无法获取足够的先验信息;再次,当解交织场景中IPS配置数量较多时,需采用更先进的NMT方法以捕捉特征,且模型需具备推理能力并可通过并行计算实现,以满足现代电磁接收机的实时处理需求;最后,未来可基于本文提出的数学表示,通过类比将雷达应用或其他领域的现有方法应用于雷达截获领域,或构建相应的数学框架。
附录 五种场景的数据准备方法
A. 场景1:参数固定的常规雷达
该场景为简单解交织任务,源以参数层面表示,训练集和测试集的模型参数均完全已知。首先生成每个源的脉冲序列,再基于其对应的到达时间(TOA)得到混合脉冲序列;在交织过程中,为模拟雷达辐射源的活跃时间,每个源脉冲序列的第一个TOA随机设置为初始相位。
B. 场景2:无模式切换的多功能雷达(MFR)
如第二节A2所述,调制层面设置可体现多功能雷达(MFR)或认知雷达(CR)在选择或优化调制参数方面的灵活性。对于无模式切换的MFR解交织,序列通过在每个MFR的空间(包括调制类型和调制参数空间)中随机采样模型生成,且每个源的相位也会变化。
C. 场景3:含模式切换的多功能雷达(MFR)
该场景中,交织脉冲序列存在模式切换,即部分或全部源的脉冲序列包含多个连续的雷达工作模式。基于P的IPS配置,可为此场景设计预处理流程:假设存在K个源,每个源包含MkM_{k}Mk(1≤Mk<+∞1 ≤M_{k}<+\infty1≤Mk<+∞)种可能的工作模式,每种工作模式由参数模型Θkm\Theta_{k}^{m}Θkm(1≤m≤Mk1 ≤m ≤M_{k}1≤m≤Mk)表示;若每次所有源均发射MkM_{k}Mk种模式中的一种,则P的IPS配置总数为∏k=1KMk\prod_{k=1}^{K} M_{k}∏k=1KMk。当这些雷达存在模式切换时,针对此类IPS解交织的两种数据准备方法如下:
图13(a)展示了MFR A和B的交织序列生成过程,每个MFR分别有两种工作模式(A1、A2和B1、B2)。(b)为两种数据准备方法。
第一种数据准备方法如图13(b)所示:首先,根据文献[51]中的步骤分别准备每个分量源的模式切换序列;然后,为包含多个模式切换的样本分配随机初始相位,并手动生成交织序列;在交织脉冲序列中,同一源的脉冲无论属于哪种工作模式,均标记为相同的雷达标签(例如,A1、A2、A3中的脉冲均标记为类别标签“A”)。
第二种数据准备方法:首先生成P的所有∏k=1KMk\prod_{k=1}^{K} M_{k}∏k=1KMk种IPS配置样本;然后,将每个样本中所有∏k=1KMk\prod_{k=1}^{K} M_{k}∏k=1KMk种IPS配置样本拼接成单个序列;拼接时,随机排列各配置样本的顺序以生成多个训练样本(注:单个序列中每种配置只需出现一次)。
由于现有研究均未考虑此类交织脉冲序列的解交织,本文通过实验设计了数据驱动方法,并在实验部分对两种提出的数据准备方法进行了评估与比较。需注意,测试阶段每个源的发射模式数量可变化,即每个雷达可随机发射其工作模式,无需在单个IPS样本中发射所有模式;这种能力得益于seq2seq学习对配置间和配置内特征的学习。
D. 场景4:无模式切换且活跃数量可变的多功能雷达(MFR)
该场景中,假设候选雷达总数K已知,但每个时刻活跃雷达数量k(1≤k≤K1 ≤k ≤K1≤k≤K)未知。根据P的IPS配置定义,当k从1变化到K时,P的可能IPS配置总数为2K−12^{K}-12K−1。借鉴场景3中第二种数据准备方法的拼接思路,将这2K−12^{K}-12K−1种可能的P的IPS配置按随机顺序拼接,形成训练样本;测试阶段,训练后的模型可正确解交织k可变的IPS。该数据准备方法如图14所示。
图14 活跃辐射源数量可变场景的数据准备方法示意图(场景中的候选雷达及完整IPS配置集:k=1时为雷达A单独、雷达B单独、雷达C单独;k=2时为A与B混合、A与C混合、B与C混合;k=3时为A、B、C混合;最终形成含七种IPS配置的交织序列)。
E. 场景5:模型相同的雷达
对于监督分类器而言,混合雷达的所有PDW序列完全相同,因此无法在高维PDW空间中解交织各源;唯一可行的解交织方式是利用每个源的PRI信息,但由于PRI相同,分类器会面临固有矛盾。以两个模型相同的源“A”和“B”为例:由于二者完全相同,交换“A”和“B”的标签不会影响结果,这种情况会使监督分类器产生混淆,导致无法正常训练。
基于P的IPS配置,相同源之间的唯一差异在于其在IPS中的初始相位。因此,训练样本中每个源的初始相位空间不应重叠;在此条件下,可基于不同的初始相位区分“A”和“B”,监督分类器也能正常训练;测试阶段,训练后的分类器可正确提取同一雷达的脉冲。
 基于神经机器翻译的雷达脉冲解交织
基于神经机器翻译的雷达脉冲解交织























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










