LeetCode算法学习笔记——二叉树与图

二叉树是子节点小于等于2的树。

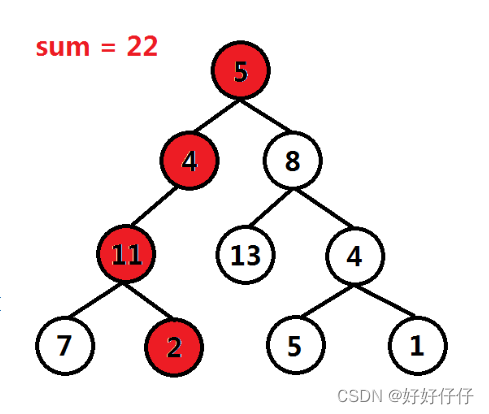
1.        给定一个二叉树于整数sum，找出所有从根节点到叶节点的路径，这些路径上的节点值累加和为sum。

分析：

1. 深度遍历二叉树，需要用一个容器存储节点的值，使用vector容器path，使用path_value累加节点值

2. 遍历到叶节点时，检查path_value，若为sum，加入到result

3. 一条路径的遍历中发现如果不满足要求，清空path_value和path

注：return返回当前函数的结果，不影响外面大函数的运行

#include<vector>
#include<stdio.h>
struct TreeNode{
  int val;
  TreeNode * left;
  TreeNode * right;
  TreeNode(int x):val(x),left(NULL),right(NULL){};
};
class Solution{
public:
  std::vector<std::vector<int>> pathSum(TreeNode* root,int sum){
   std::vector<std::vector<int>> result;
   std::vector<int> path;
   int path_value=0;
   preorder(root,path_value,sum,path,result);
   return result;    
  }
private:
  void preorder(TreeNode* node,int &path_value,int sum,std::vector<int> &path,std::vector<std::vector<int>> &result){
    if(node==nullptr)
    return;
    path_value+=node->val;
    path.push_back(node->val);
    if (node->left==nullptr&&node->right==nullptr&&path_value==sum)
    {
      result.push_back(path);
    }
    preorder(node->left,path_value,sum,path,result);
    preorder(node->right,path_value,sum,path,result);
    path_value-=node->val;
    path.pop_back();
  }
};

2. 最近的公共祖先

已知二叉树，求二叉树中给定的两个节点的最近公共祖先。

最近公共祖先：树上最低（离根最远）

分析：深度搜索

1. 从根节点遍历，找到后结束搜索

2. 按顺序存储节点

void preorder(TreeNode* node,TreeNode* search,std::vector<TreeNode*> &path,std::vector<TreeNode*> &result,int &finish){
    if(node==nullptr||finish==1)
    return;
    path.push_back(node);
    if (node==search)
    {
      finish=1;
      result=path;
    }
    preorder(node->left,search,path,result,finish);
    preorder(node->right,search,path,result,finish);
    path.pop_back();
  }

1. 求路径的长度n

2. 同时遍历p和q，最后一个的相同节点，即最近公共祖先

 3.        给定一个二叉树，将该二叉树按前序遍历的顺序转换成单链表

分析：

按顺序遍历vector，将前面的节点左指针置空，右指针与后面节点相连

#include<stdio.h>
struct TreeNode{
  int val;
  TreeNode * left;
  TreeNode * right;
  TreeNode(int x):val(x),left(NULL),right(NULL){};
};
class Solution{
public:
  void flatten(TreeNode * root)
  {
    std::vector<TreeNode* > node_vec;
    preorder(root,node_vec);
    for (int i = 1; i < node_vec.size(); i++)
    {
      node_vec[i-1]->left=nullptr;
      node_vec[i-1]->right=node_vec[i];
    }   
  }
private:
  void preorder(TreeNode* node,std::vector<TreeNode* > node_vec){
    if(node==nullptr)
    return;
    node_vec.push_back(node);
    preorder(node->left,node_vec);
    preorder(node->right,node_vec);
  }
};

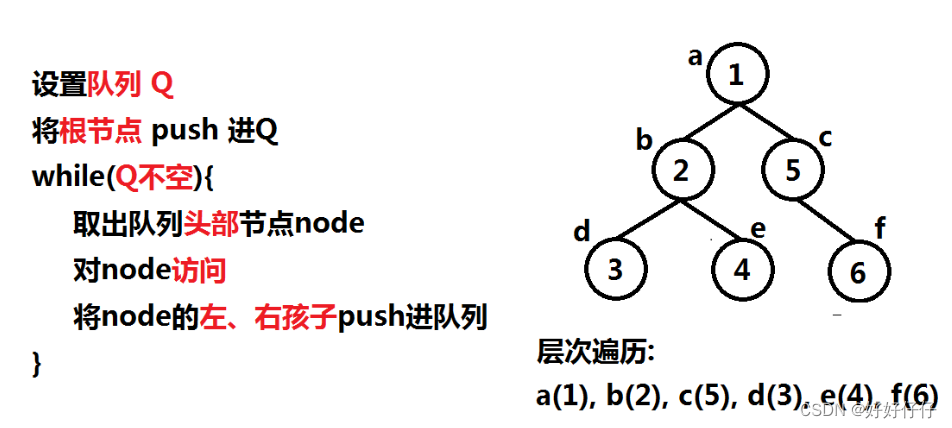
宽度优先遍历

#include<vector>
#include<stdio.h>
#include<queue>
struct TreeNode{
  int val;
  TreeNode * left;
  TreeNode * right;
  TreeNode(int x):val(x),left(NULL),right(NULL){};
};
void BFS_print(TreeNode* root)
{
  std::queue<TreeNode *> Q;
  Q.push(root);
  while (!Q.empty())
  {
    TreeNode *node=Q.front();
    Q.pop();
    printf("");
    if (node->left!=nullptr)
    {
      Q.push(node->left);
    }
    if (node->right!=nullptr)
    {
      Q.push(node->right);
    }  
  }
}

深度优先算法

参考：

https://blog.youkuaiyun.com/weixin_43272781/article/details/82959089

void dfs(int step)
{
        判断边界
        {
            相应操作
        }
        尝试每一种可能
        {
               满足check条件
               标记
               继续下一步dfs(step+1)
               恢复初始状态（回溯的时候要用到）
        }
}