ResNet与梯度消失 与 batch normalization

1 梯度消失问题

1.1 sigmoid当中的梯度消失

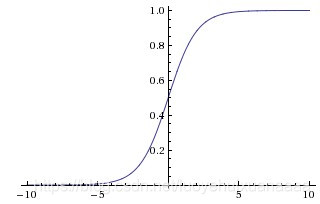
上图是sigmoid的函数图像，这个函数可以增加非线性性，但是当输入值足够大或者足够小的时候，输出值基本上不变，这个时候函数的梯度值基本上就是0，这就达不到梯度下降的功能了。

1.2 用ReLU代替sigmoid

为了解决这个问题，引入了新的非线性单元，ReLU。表达式也非常简单，可以看到，不管输入值多大，梯度值都是存在的，这就在一定程度上解决了梯度消失的问题，因而ReLU也比sigmoid在性能上更好。

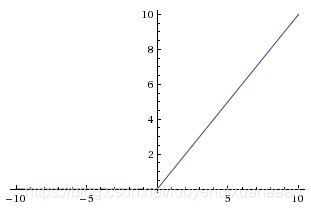
1.3 连乘导致的梯度消失问题

因为梯度连乘的问题，梯度消失的问题依然存在。我们通过正常的back propagation进行计算

但是这个时候，如果网络很深很深，就会出现这样的情况：

这个时候再做back propagation求偏导的话，就是

这个偏导就是我们求的gradient，这个值本来就很小，而且再计算的时候还要再乘stepsize，就更小了。所以可以看到，梯度在反向传播过程中的计算，如果N很大，那么梯度值传播到前几层的时候就会越来越小，也就是梯度消失的问题。

2 ResNet怎样解决了梯度消失问题

它将基本的单元改成了这个样子

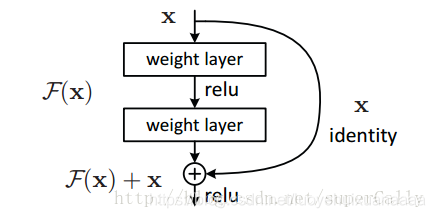
其实也很明显，通过求偏导，我们可以看到：

这样就算深度很深，梯度也不会消失了。

正是由于多了这条捷径，来自深层的梯度能够直接畅通无阻的通过，去到上一层，使得浅层网络层参数得到有效的训练。

3 Batch Normalization

https://baijiahao.baidu.com/s?id=1621528466443988599&wfr=spider&for=pc

对于小批量，BN会降低性能，所以要避免太小的批量，才能保证批归一化的效果

对于具有分布极不平衡的二分类测试任务，也不要使用BN

BN解决了梯度消失的问题

BN使得模型正则化，BN算法后，参数进行了归一化，不用太以来drop out、L2正则化解决归一化，采用BN算法后可以选择更小的L2正则约束参数，因为BN本身具有提高网络泛化能力的特性。