顺序表类型
1.顺序表类型由两部分组成
能够使用数组,也可以使用堆区空间
一个能标识顺序表实际长度的变量
2.有关顺序表长度的变量
表示顺序表的实际长度
表示容器中第一个没有存储数据元素的数组元素下标
#define MAX 100 //宏定义顺序表最大长度
typedef int datatype; //数据元素类型
//定义顺序表类型
typedef struct
{
datatype data[MAX]; //存储顺序表的数组容器
int len; //存储顺序表的长度
}SeqList, *SeqList_ptr;
顺序表的创建
1.在堆区空间创建一个顺序表,使用函数封装
可以使用函数形参返回顺序表地址: void list_create(SeqList_ptr *s)
可以使用函数的返回值返回顺序表地址:SeqList_ptr list_create(void)
2.在堆区申请空间后,可以给内存空间初始化,也可以不用初始化
顺序表的长度必须初始化为0
3.函数介绍:从堆区空间申请出一个顺序表的空间大小,并将该堆区空间返回给主调函数使用
参数:无
返回值:堆区申请出来的顺序表的起始地址
//创建顺序表的定义
SeqList_ptr list_create()
{
//在堆区申请一个顺序表
SeqList_ptr S = (SeqList_ptr)malloc(sizeof(SeqList));
if(NULL == S)
{
printf("创建顺序表失败\n");
return NULL;
}
//程序执行至此,表示创建成功
//给顺序表进行初始化
bzero(S->data, sizeof(datatype)*MAX); //初始化数组
S->len = 0; //顺序表长度为0
printf("顺序表创建成功\n");
return S;
}
顺序表判空和判满
1.当需要向顺序表中添加元素时,需要先判断是否已经满了,如果已经满了,则添加失败
2.当需要从顺序表中删除数据元素时,需要判断顺序表是否判断是否已经空了,删除失败
3.判空函数:判断给定的顺序表是否为空
参数:顺序表的起始地址
返回值:1表示空,0表示非空
4.判满函数:判断给定的顺序表是否已经满了
参数:顺序表的起始地址
返回值:1表示满,0表示非满
//判断顺序表是否为空
int list_empty(SeqList_ptr S)
{
//判断传入的顺序表是否合法
if(NULL==S)
{
printf("非法顺序表\n");
return 0; //后续不能操作
}
//判断顺序表长度
return 0==S->len ? 1:0;
}
//判断顺序表是否满了
int list_full(SeqList_ptr S)
{
//判断传入的顺序表是否合法
if(NULL==S)
{
printf("非法顺序表\n");
return 1; //后续不能操作
}
//判断顺序表长度是否为最大长度
return S->len == MAX ? 1:0;
}
向顺序表中添加数据
1.功能:将给定的数据,放入到给定的顺序表中
参数:顺序表起始地址,要添加的元素
返回值:成功添加返回0,失败返回-1
2.函数解析:
1.当顺序表没有满的情况下进行添加操作
2.可以将元素添加到当前数据表长度指示的数组下标位置处
3.数组长度增加
//向顺序表中添加元素
int list_add(SeqList_ptr S, datatype e)
{
//判断合法性
if(list_full(S))
{
printf("顺序表已满,添加失败\n");
return -1;
}
//添加逻辑
S->data[S->len] = e;
//表长变化
S->len++;
printf("添加成功\n");
return 0;
}
遍历顺序表
1.功能:将顺序表中的内容全部输出,从下标为0开始到顺序表长度处结束
参数:顺序表其实地址
返回值:无
2.先判定是否为空
//查看顺序表内容函数
void list_show(SeqList_ptr S)
{
//判空
if(list_empty(S))
{
printf("查看失败\n");
return ;
}
//遍历整个顺序表
printf("当前顺序表中数据分别是:");
for(int i=0; i<S->len; i++)
{
printf("%d\t", S->data[i]);
}
printf("\n");
}
顺序表任意位置插入
功能:在顺序表任意位置进行插入给定的数据
参数:顺序表起始位置,要插入的位置,要插入的元素
返回值:成功返回0,失败返回-1
顺序表满了,插入失败
顺序表插入的位置小于0,或者大于len都不合法
核心逻辑:
要插入的位置数据到最后一个数据整体向后移动一格
要求从后向前依次向后移动
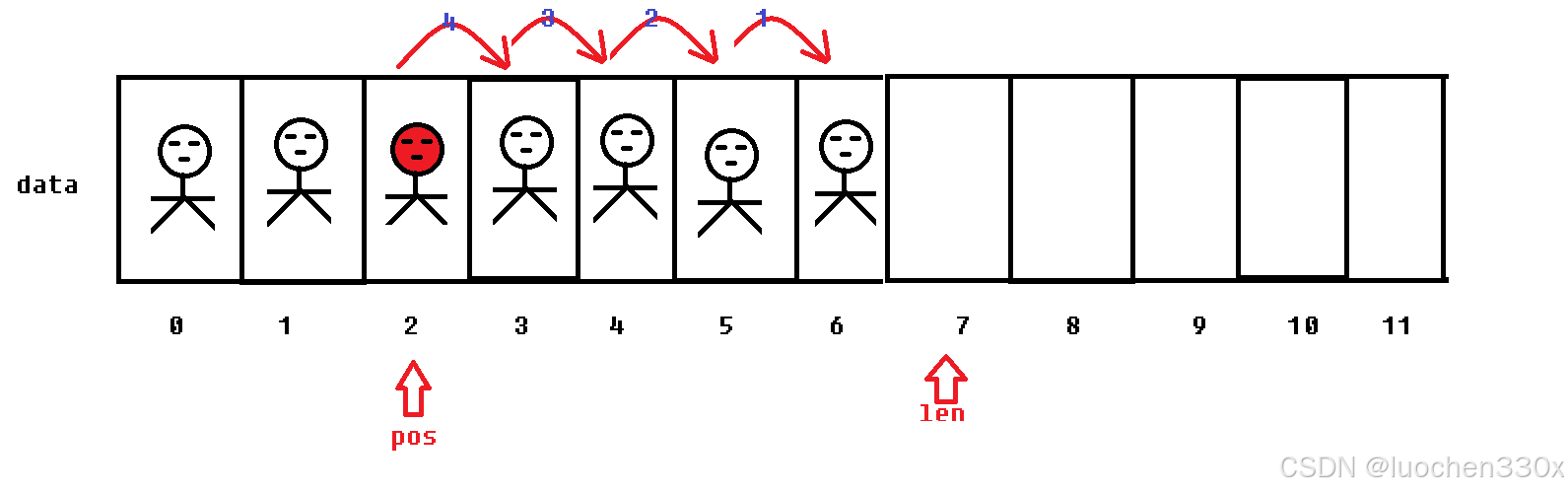
//顺序表按任意位置进行插入操作
int list_insert_pos(SeqList_ptr S, int pos, datatype e)
{
//判断逻辑
if(list_full(S) || pos<0 || pos>S->len)
{
printf("插入失败\n");
return -1;
}
//腾空逻辑
for(int i=S->len-1; i>=pos; i--)
{
S->data[i+1] = S->data[i]; //将当前元素向后放
}
//将数据放入顺序表
S->data[pos] = e;
//表长变化
S->len++;
printf("插入成功\n");
return 0;
}
顺序表任意位置删除
1.功能:在给定的顺序表中删除指定位置上的元素
2.参数:顺序表起始地址,要删除的位置
3.返回值:成功返回0,失败返回-1
注意事项
顺序表为空时,删除失败
给定的删除位置不合法时,也删除失败 位置小于0或者位置大于等于len
核心逻辑:将从要删除位置元素到顺序表最后一个元素,整体前移一格
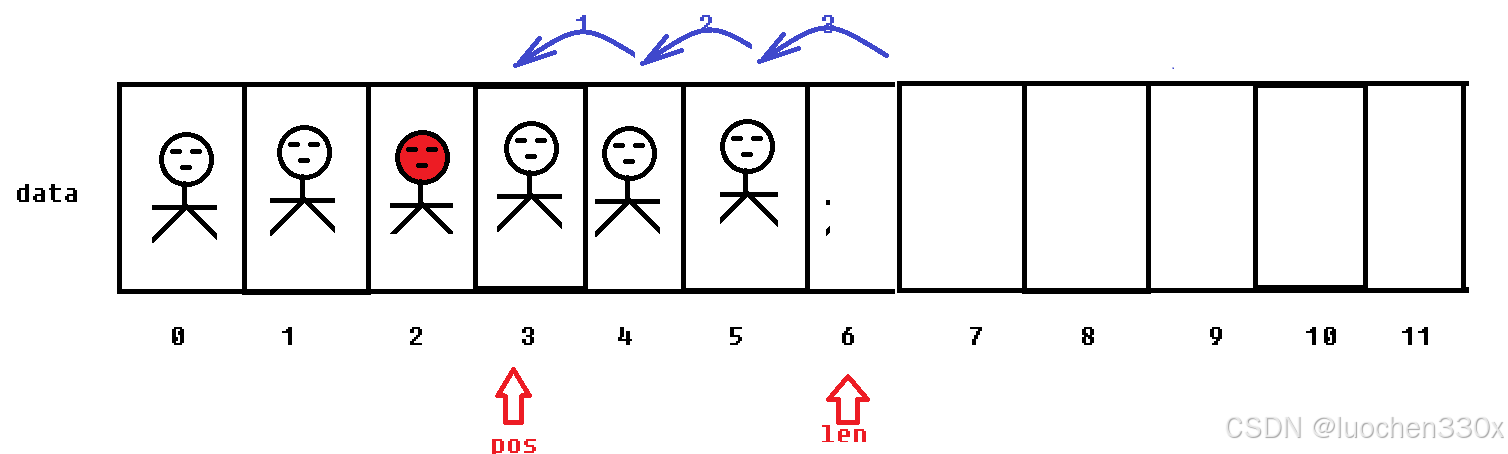
//顺序表按位置进行删除
int list_delete_pos(SeqList_ptr S, int pos)
{
//判断逻辑
if(list_empty(S) || pos<0 || pos>=S->len)
{
printf("删除失败\n");
return -1;
}
//删除逻辑
for(int i=pos+1; i<S->len; i++)
{
S->data[i-1] = S->data[i];
}
/*
for(int i=pos; i<S->len-1; i++)
{
S->data[i] = S->data[i+1];
}*/
//表长变化
S->len--;
printf("删除成功\n");
return 0;
}
顺序表按值查找返回元素下标
功能:通过给定的值,查找该值是否存在于顺序表中,如果存在,则返回该元素的下标
参数:顺序表起始地址,要查找的值
返回值:成功查找到返回值对应的下标,失败返回-1
//顺序表按值查找返回位置
int list_search_value(SeqList_ptr S, datatype e)
{
//判断逻辑
if(list_empty(S))
{
printf("查找失败\n");
return -1;
}
//处理逻辑
for(int i=0; i<S->len; i++)
{
//判断是否跟任意一个元素相等
if(S->data[i] == e)
{
return i;
}
}
printf("查找失败\n");
return -1; //表示没找到
}
顺序表按值修改值
功能:判断旧值是否存在于数组中,如果存在更改新值
参数:顺序表起始地址,要查询的旧值,要被更新的新值
返回值:成功修改返回0,失败返回-1
逻辑:通过旧值找到旧值对应的下标,通过下标修改数据新值
//顺序表按值进行修改
int list_update_value(SeqList_ptr S, datatype old_e, datatype new_e)
{
//判断逻辑
if(list_empty(S))
{
printf("修改失败\n");
return -1;
}
//通过旧值查找旧值的位置
int res = list_search_value(S, old_e);
if(res == -1)
{
printf("更新失败\n");
return -1;
}
//程序执行至此,res表示的就是要修改的值的下标
S->data[res] = new_e;
printf("修改成功\n");
return 0;
}
顺序表去重
功能:去重顺序表中重复的元素,保持顺序表中的每个数据都是唯一的
参数:顺序表起始地址
返回值:成功返回0,失败返回-1
注意事项:当顺序表的长度小于或者等于0时,无需去重
//顺序表去重操作
int list_unique(SeqList_ptr S)
{
//判断逻辑
if(list_empty(S) || S->len==1)
{
printf("去重失败\n");
return -1;
}
//去重逻辑
for(int i=0; i<S->len; i++) //遍历所有元素
{
//找到任意一个元素 S->data[i]
for(int j=i+1; j<S->len; j++) //遍历 S->data[i]后面的元素
{
if(S->data[i] == S->data[j])
{
//说明有重复的元素
list_delete_pos(S, j); //删除下标为j的元素
j--; //防止漏网之鱼
}
}
}
printf("去重成功\n");
return 0;
}
销毁顺序表
功能:销毁顺序表,将堆区空间释放,并将指针置空
参数:顺序表起始地址
返回值:无
注意事项:注意指针的传递和地址传递
//顺序表销毁
void list_destroy(SeqList_ptr S)
{
if(NULL != S)
{
//销毁顺序表
free(S);
S = NULL;
}
printf("销毁成功\n");
}
#include <luochen.h>
#include "seqlist.h"
//创建顺序表的定义
seqlist_p list_create()
{
seqlist_p s=(seqlist_p)malloc(sizeof(seqlist));
if (NULL==s)
{
printf("创建顺序表失败\n");
return NULL;
}
//给顺序表进行初始化
bzero(s->data,sizeof(datatype)*MAX);
s->len=0;
printf("顺序表创建成功\n");
return s;
}
int list_empty(seqlist_p s)
{
//判断顺序表是否合法
if(NULL==s)
{
printf("非法顺序表\n");
return 0;
}
//判断顺序表长度
return 0==s->len ? 1:0;
}
int list_full(seqlist_p s)
{
//判断是否合法
if(NULL==s)
{
printf("非法顺序表\n");
return 1;
}
//判断长度是否为最大值
return s->len==MAX ? 1:0;
}
int list_add(seqlist_p s, datatype e)
{
//顺序表添加数据
//判断合法性
if(list_full(s))
{
printf("顺序表已满,添加失败\n");
return -1;
}
//添加逻辑
s->data[s->len] = e;
//表长变化
s->len++;
printf("添加成功\n");
return 0;
}
void list_show(seqlist_p s)
{
//判空
if(list_empty(s)||NULL==s)
{
printf("查看失败\n");
return ;
}for (int i=0;i<s->len;i++)
{
printf("%d\t",s->data[i]);
}printf("\n");
}
int list_pos(seqlist_p s,int pos,datatype e)
{ //判断逻辑
if(list_full(s)||pos>s->len||pos<0)
{
printf("插入失败\n");
return -1;
}//插入//添加元素
for (int i=s->len-1;i>=pos;i--)
{
s->data[i+1]=s->data[i];
}s->data[pos]=e;
s->len++;
printf("插入成功\n");
return 0;
}
int list_delata_pos(seqlist_p s,int pos)
{
//任意位置删除
if(list_empty(s)||pos<0||pos>s->len)
{
printf("删除失败\n");
return -1;
}for (int i=pos;i<s->len-1;i++)
{
s->data[i]=s->data[i+1];
}s->len--;
printf("删除成功\n");
return 0;
}
int list_search_value(seqlist_p s,datatype e)
{
if(list_empty(s))
{
printf("查找失败\n");
return -1;
}
//处理逻辑
for (int i=0;i<s->len;i++)
{
//判断是否相等
if(s->data[i]==e)
return i;
}
printf("查找失败\n");
return -1;
}
int list_update_value(seqlist_p s,datatype old_e,datatype new_e)
{
if(list_empty(s))
{
printf("修改失败\n");
return -1;
}
int res=list_search_value(s,old_e);
if(res==-1)
{
printf("更新失败\n");
return -1;
}
s->data[res]=new_e;
printf("修改成功\n");
return 0;
}
//顺序表去重操作
int list_unique(seqlist_p s)
{
if(list_empty(s)||s->len==1)
{
printf("去重失败\n");
return -1;
}
for (int i=0;i<s->len;i++)
{
for(int j=i+1;j<s->len;j++)
{
if(s->data[i]=s->data[j])
{
list_delata_pos(s,j);
//删除下标为j的元素
j--;//防止漏网之鱼
}
}
}
printf("去重成功\n");
return 0;
}
void list_destory(seqlist_p s)
{
if(NULL!=s)
{
free(s);
s=NULL;
}printf("销毁成功\n");
}
int list_pos_search(seqlist_p s,int pos)
{
if(list_empty(s)||pos<0||pos>=s->len)
{
printf("修改失败\n");
return -1;
}
//顺序表按位置查找返回元素值
return s->data[pos];
}
int list_pos_update(seqlist_p s,int pos,datatype e)
{
if(list_empty(s)||pos<0||pos>=s->len)
{
printf("修改失败\n");
return -1;
}
//顺序表按位置进行修改元素
s->data[pos]=e;
return 0;
}
int list_sort(seqlist_p s)
{
if(list_empty(s)||s->len==1)
{
return-1;
}
//冒泡排序从小到大
for (int i=1;i<s->len;i++)
{
for (int j=0;j<s->len-i;j++)
{
if(s->data[j]>s->data[j+1])
{
int temp=s->data[j];
s->data[j]=s->data[j+1];
s->data[j+1]=temp;
}
}
}printf("排序成功\n");
return 0;
}
int fanzhuan(seqlist_p s)
{
//顺序表翻转
if(list_empty(s)||s->len==1)
{
return-1;
}
for (int i=0;i<s->len/2;i++)
{
datatype temp =s->data[i];
s->data[i]=s->data[s->len-i-1];
s->data[s->len-1-i]=temp;
}
return 0;
}




















 579
579

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








