创智2025-A班集训7月30日模拟赛补题报告

比赛时间

2025 - 7 - 30 \quad 18：00 - 21：00

比赛过程

果断放弃 A，在 B 题写了超长的暴力（居然只有 $10$ 分），然后探究 C 题的规律（探了个寂寞），心态崩了所以没写 D 题 。

A.无聊的字符串（string）

得分：$0pts$。

题面

【题目描述】

你的手头有一个非常无聊的字符串 $S$，它的长度是 $n$。

这个字符串的无聊之处在于，这个字符串只会含有由 A、B、C、D 这四个字符。当然，这四个字符也有可能不都出现。

你对这个无聊的字符串特别不满意。现在，你被赋予了一种魔法。有了该魔法，你可以用以下两种方式修改这个字符串：

• 选择 $S$ 中任意两个相邻的字符，交换它们。
• 除了第一种方式，题目还会给你 $m$ 个转移。一个转移是一组长度相等且不超过 $n$ 的字符串 $a_i$ 和 $b_i$，可以把 $S$ 中的一个子串 $a_i$ 替换成 $b_i$。

在一次魔法中，你可以选择任何一种转移。如果你使用了多次魔法，多次魔法中选择的转移不必相同。

现在，你想知道，如果初始字符串 $S$ 任意选，并且你可以用任何次数的魔法，那么你最多能变出多少种不同的字符串（包含初始字符串 $S$）？

【输入格式】

第一行两个整数 $n$ 和 $m$，表示初始字符串的长度和转移的个数。 后面m行每行两个字符串 $a_i$ 和 $b_i$，描述一个转移。

【输出格式】

一行一个整数，表示答案。保证答案在 C++ 的 long long 范围内。

思路

谁家好人第一题考 tarjan 啊！

用一个四元组 $(A,B,C,D)$ 来表示一个状态，那么所有字符串都能被表示。这样一共有 $n^3$ 个状态。每个状态的权值是 $\frac{n!}{A!B!C!D!}$。

$m$ 条转移就变成了四元组之间的转移，只要判断 $(A,B,C,D)$ 四个数是否都不小于 $a_i$ 转移中四个对应值就可以了。

对于一个强连通分量里的点，显然可以从任一个点进去，到达所有点，从任一个点出来。所以可以把强连通分量缩起来，权值设置成里面所有点的点权和。缩完强连通分量之后，整个图是一个有向无环图，可以用拓扑排序算出带权的最长链。

题解

#include <bits/stdc++.h>
#define int long long
using namespace std;
int n, m;
int C[40][40];
struct node {
    int c[4];
    bool operator < (const node & t) const {
        return tie(c[0], c[1], c[2], c[3]) < tie(t.c[0], t.c[1], t.c[2], t.c[3]);
    }
    node operator + (const node & t) const {
        return {c[0] + t.c[0], c[1] + t.c[1], c[2] + t.c[2], c[3] + t.c[3]};
    }
    node operator - (const node & t) const {
        return {c[0] - t.c[0], c[1] - t.c[1], c[2] - t.c[2], c[3] - t.c[3]};
    }
};
vector <int> G[5605], G1[5605]; // G 是原图，G1 是缩点后的图
map <node, int> id;
bool vis[5605];
int dfn[5605], low[5605], T;
int fa[5605], num;
stack <int> st;
int val[5605], scc_val[5605];
int deg[5605], dp[5605];
void tarjan(int u) { // tarjan 模版
    dfn[u] = low[u] = ++T;
    st.push(u);
    vis[u] = true;
    for (auto v : G[u]) {
        if (!dfn[v]) tarjan(v), low[u] = min(low[u], low[v]);
        else if (vis[v]) low[u] = min(low[u], dfn[v]);
    }
    if (dfn[u] == low[u]) {
        num++;
        int t;
        do {
            t = st.top(), st.pop();
            vis[t] = false, fa[t] = num;
            scc_val[num] += val[t];
        } while (t != u);
    }
}
signed main() {
    cin >> n >> m;
    C[0][0] = 1;
    for (int i = 1; i <= n; i++) { // 杨辉三角
        C[i][0] = C[i][i] = 1;
        for (int j = 1; j < i; j++) C[i][j] = C[i - 1][j] + C[i - 1][j - 1];
    }
    for (int a = 0; a <= n; a++) 
        for (int b = 0; a + b <= n; b++)
            for (int c = 0; a + b + c <= n; c++) {
                int d = n - a - b - c, x = id.size() + 1;
                id[{a, b, c, d}] = x;
                val[x] = C[n][a] * C[n - a][b] * C[n - a - b][c];
            }
    int tot = id.size();
    while (m--) {
        string a, b;
        cin >> a >> b;
        node u = {0, 0, 0, 0}, v = {0, 0, 0, 0}; // 记得初始化（卡了我好久）
        for (auto c : a) u.c[c - 'A']++;
        for (auto c : b) v.c[c - 'A']++;
        for (auto [now, idx] : id) {
            bool ok = true;
            for (int i = 0; i < 4; i++) if (u.c[i] > now.c[i]) ok = false;
            if (ok && id.count(now - u + v)) G[idx].push_back(id[now - u + v]);
        }
    }
    for (int i = 1; i <= tot; i++) if (!dfn[i]) tarjan(i); // tarjan 缩点
    for (int i = 1; i <= tot; i++) { // 建新图
        for (auto j : G[i]) if (fa[i] != fa[j]) G1[fa[j]].push_back(fa[i]); 
    }
    for (int i = 1; i <= num; i++) for (auto j : G1[i]) deg[j]++;
    queue <int> q;
    for (int i = 1; i <= num; i++) if (!deg[i]) q.push(i), dp[i] = scc_val[i];
    while (!q.empty()) { // 拓扑排序
        int u = q.front();
        q.pop();
        for (auto v : G1[u]) {
            dp[v] = max(dp[v], scc_val[v] + dp[u]);
            if (!(--deg[v])) q.push(v);
        }
    }
    int ans = 0;
    for (int i = 1; i <= num; i++) ans = max(ans, dp[i]);
    cout << ans << "\n";
    return 0;
}

B.住宅区与工业区（city）

得分：$10pts$。

题面

【题目描述】

M 市正在进行城市规划。

M 市的面积很大。在本题中，我们将M市视为一个无限大的二维平面。在这个二维平面中，一个 $1\times 1$ 面积大小的土地算一块区域。在此次城市规划中，管理者将城市的所有区域分成住宅区和工业区。为了更方便居民的出行，同时也为了让工业园区之间的交通更加便利，M 市的规划方案满足以下条件：

• 定义区域 $(i,j)$ 与区域 $(i-1,j)$、$(i+1,j)$、$(i,j-1)$ 和 $(i,j+1)$ 相邻。 从一个住宅区出发，可以前往相邻的住宅区；从一个工业区出发，可以前往相邻的工业区。
• 对于任意两个住宅区 $x$ 和 $y$，从 $x$ 出发都能到达 $y$，且途中只经过住宅区。
• 对于任意两个工业区 $x$ 和 $y$，从 $x$ 出发都能到达 $y$，且途中只经过工业区。

比如，如果用黄色表示住宅区，白色表示工业区，那么以下几种规划方案都是不合法的。

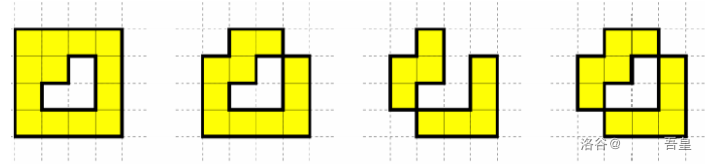
从任何一个住宅区走到相邻住宅区所用的时间都是 $1$。设 $d(v_i,v_j)$ 表示住宅区 $v_i$ 与住宅区 $v_j$ 之间的距离，它指的是从住宅区 $v_i$ 走到住宅区 $v_j$ 所需要的最短时间。如下图中 $d(v_1,v_3)=1,d(v_6,v_{10})=2,d(v_9,v_{10})=4,d(v_1,v_8)=6$ 。

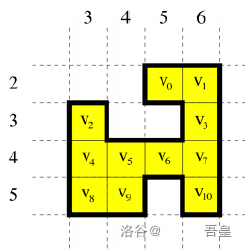
从任何一个住宅区走到相邻住宅区所用的时间都是 $1$。设 $d(v_i,v_j)$ 表示住宅区 $v_i$ 与住宅区 $v_j$ 之间的距离，它指的是从住宅区 $v_i$ 走到住宅区 $v_j$ 所需要的最短时间。

设M市一共有 $n$ 个住宅区，分别是 $v_0,v_1,\cdots ,v_{n-1}$。题目会给定这 $n$ 个住宅区的坐标 $(x_0,y_0),(x_1,y_1),\cdots ,(x_{n-1},y_{n-1})$，其他的区域都是工业区。你的任务是，计算出任意两个住宅区之间的距离之和，也就是 $$\sum _{i=0}^{n-5}\sum _{j=i+1}^{n-1}d(v_i,v_j)$$

【输入格式】

第一行，一个正整数 $n$。 接下来 $n$ 行，每行两个正整数 $(x_i,y_i)$，表示每个住宅区的坐标。

【输出格式】

一行一个整数，表示答案。 由于这个答案可能很大，你只需要输出对 $10^9$ 取模后的值。

思路

这题居然来自 IOI！洛谷紫题！但我感觉像蓝题。

把 $x$ 坐标相同的连续“横条”看成一个点，把有接触的“横条”连上边，就得到了是一棵树。在这棵树上作树形 dp。

题解

#include <bits/stdc++.h>
#define int long long
#define pii pair<int,int>
using namespace std;
const int mod = 1e9;
int n, ans, x[100005], y[100005], sz[100005];
map <pii, int> mp;
vector <pii> G[100005];
void dfs(int u, int fa) {
    sz[u] = 1;
    for (auto [v, id] : G[u]) {
        if (v != fa) {
            dfs(v, u);
            ans = (ans + sz[v] * (n - sz[v]) % mod * id % mod) % mod;
            sz[u] = (sz[u] + sz[v]) % mod;
        }
    }
}
signed main() {
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> x[i] >> y[i];
    for (int j = 0; j <= 1; j++) {
        mp.clear();
        for (int i = 1; i <= n; i++) G[i].clear();
        for (int i = 1; i <= n; i++) swap(x[i], y[i]), mp[{x[i], y[i]}] = i;
        for (int i = 1; i <= n; i++) {
            int a = mp[{x[i] + 1, y[i]}];
            if (a) G[a].push_back({i, 0}), G[i].push_back({a, 0});
            a = mp[{x[i], y[i] + 1}];
            if (a && !(mp[{x[i] - 1, y[i]}] && mp[{x[i] - 1, y[i] + 1}])) G[a].push_back({i, 1}), G[i].push_back({a, 1});
        }
        dfs(1, 0);
    }
    cout << ans << "\n";
    return 0;
}

C.有趣的字符串（fun）

得分：$0pts$。

题面

【题目描述】

小M在无聊的字符串一题中，发现了两个字符串特别有意思。小M将其称为 $S$ 和 $T$ 。$S$ 与 $T$ 都只包含 a、b、c 三个字母，而且 $S$ 和 $T$ 的长度相等，都是 $L$。

解决完无聊的字符串一题后，小M发现字符串的变换非常有意思。因此，他想去思考一个稍微难一点的问题。在这个问题中，$S$ 中的 a 可以变成 b，b 又可以变成 c，c 又可以变成 a。但是，小$M$ 并没有太多耐心将字符串 $S$ 变来变去。因此，他制定了一个变化规则：

• 将字符串 $S$ 中的任意一个 a 变成 b，会消耗他 $c_1$ 点耐心值。
• 将字符串 $S$ 中的任意一个 b 变成 c，会消耗他 $c_2$ 点耐心值。
• 将字符串 $S$ 中的任意一个 c 变成 a，会消耗他 $c_3$ 点耐心值。

小 M 一共有 $n$ 点耐心值。现在，小 M 想知道，在消耗不超过 $n$ 点耐心值的前提下，他有多少种不同的操作序列能将 $S$ 变成 $T$。

两种操作序列 $A$ 和 $B$ 被认为是不同的，要么操作数量不同，要么对于第 $k$ 步操作，方案 $A$ 修改了位置 $i$，方案 $B$ 修改了位置 $j(i\ne j)$。在 $S$ 变成 $T$ 的过程中， $T$ 可以出现多次，即不是一变成 $T$ 就必须停止变换。

【输入格式】

第一行一个字符串 $S$。 第二行一个字符串 $T$。 第三、四、五行三个整数 $c_1,c_2,c_3$。 第六行一个整数 $n$。

【输出格式】

一行一个整数，表示答案。 由于这个答案可能很大，你只需要输出对 $10^9+7$ 取模后的值。

思路

设最小的花费为 $c_0$，则任何一种可行的方案花费都一定是 $c_0+k(c_1+c_2+c_3) $，其中 $k\in \mathbb{N}$。

这个性质表面答案只与 $k$ 有关，故第 $i$ 位的操作次数 $x_i$ 和最小的操作次数 $x_{i_{min}}$ 必须满足 $x\equiv x_{min}(\mathrm{mod}3)$。

若有 $a$ 个 $x_{i_{min}}=0$，$b$ 个 $=1$，$c$ 个 $=2$，则 $a+b+c\equiv L$。

那么记 $d{p}_{i,j,k}$ 表示 $a=i,b=j,c=L-a-b$ 时消耗 $k$ 点耐心值的方案数。

（由于第三位很大，所以需要用矩阵优化）

题解

代码暂无

D.星球保卫战（guard）

得分：$0pts$。

题面

【题目描述】

Mars星球上勇敢的人们正在进行一场星球保卫战。

Mars星球上一共有 $n$ 个城市，从 $0$ 到 $n-1$ 编号。这些城市通过 $n-1$ 条双向道路连接形成一棵树。对于每一个 $i(1\le i\le n-1)$，城市 $i$ 和城市 $a_i$ 之间存在一条耗时为 $1$ 的边。因此，任意两个城市之间都有一条唯一的最短路径。

如果一个城市遭遇了袭击，该城市会派出 $n-1$ 个骑兵，分别前往其他 $n-1$ 个城市通报遭受袭击的消息，以让其他城市早点做好防御准备。有些城市之间的距离特别远，所以Mars上的统治者非常担心：一旦某个城市遭受袭击，有些城市不能很快得知消息，做好防御准备。因此，他们决定选两个城市并建造传送门（可以是同一个城市）。当骑兵在一个有传送门的城市时，他可以瞬间移动到另一个有传送门的城市。定义 $dis(i,j)$ 表示建立传送门后从城市 $i$ 到城市 $j$ 花费的最少时间。求有多少种建造传送门的方案使得 max ⁡ { d i s ( i , j ) ∣ ( 0 ≤ i , j ≤ n − 1 ) } ≤ k \max\{dis(i,j)\mid(0\le i,j\le n−1)\}\le k max{dis(i,j)∣(0≤i,j≤n−1)}≤k（$(a,b)$ 和 $(b,a)$ 被视为同一种方案）

【输入格式】

第一行两个整数表示 $n$ 和 $k$。 接下来一行 $n-1$ 个数表示 $a_i(1\le i\le n-1)$。

【输出格式】

一行一个数字，表示建造传送门的不同方案数。

思路

如果在 $x$ 和 $y$ 之间建传送门，那么称 $x$ 到 $y$ 的链为“主链”，其上的点记为 $v_0\sim v_t$，其中 $v_0=x,v_t=y$。记 $val[v_i]$ 表示 $v_i$ 到自己子树内的最长链的长度，它在主链上的深度为 $dep[v_i]$。

那么必须满足对于 $\forall 0\le j<i\le t$， v a l [ v i ] + v a l [ v j ] + min ⁡ { d e p [ v i ] − d e p [ v j ] , d e p [ y ] − d e p [ v i ] + d e p [ v j ] − d e p [ x ] } ≤ k val[v_i]+val[v_j]+\min\{dep[v_i]-dep[v_j],dep[y]-dep[v_i]+dep[v_j]-dep[x]\}\le k val[vi​]+val[vj​]+min{dep[vi​]−dep[vj​],dep[y]−dep[vi​]+dep[vj​]−dep[x]}≤k同时对于 $\forall 0\le i\le t$，$val[i]\le k$。

如果 $val[v_i]+val[v_j]+dep[v_i]-dep[v_j]\le k$，则无需传送门；否则必须满足 $val[v_i]+val[v_j]+dep[y]-dep[v_i]+dep[v_j]-dep[x]\le k$。即$$dep[y]\le k+dep[x]-val[v_i]-val[v_j]+dep[v_i]-dep[v_j]\text{ when }val[v_j]-dep[v_j]>k-val[v_i]-dep[v_i]$$
dfs 一遍，然后记录最小值 m = min ⁡ { k + d e p [ x ] − v a l [ v i ] − v a l [ v j ] + d e p [ v i ] − d e p [ v j ] } m=\min\{k+dep[x]-val[v_i]-val[v_j]+dep[v_i]-dep[v_j]\} m=min{k+dep[x]−val[vi​]−val[vj​]+dep[vi​]−dep[vj​]}
若 $dep[y]\le m$，还需要考虑特殊情况 $v_i=y$，即$$val[y]+val[v_j]+dep[v_j]-dep[x]\le k\text{ when }val[v_j]-dep[v_j]>k-val[y]-dep[y]$$
要用树状数组维护一下后缀最大值（$BIT[val[v_i]-dep[v_i]]=val[v_i]+dep[v_i]$），然后加个队列支持撤销即可。

题解

代码暂无

比赛总结

每题正解都不容易，但其实有很多骗分点，但我没有注意。