心中有堆

数据结构 系列博文

1. 心中有堆 https://blog.youkuaiyun.com/luo_boke/article/details/106928990
2. 心中有树——基础 https://blog.youkuaiyun.com/luo_boke/article/details/106980011
3. 心中有栈 https://blog.youkuaiyun.com/luo_boke/article/details/106982563
4. 常见排序算法解析

---

前言

堆是一颗完全二叉树，是一种经过排序的树形数据结构，它满足如下性质:

1. 堆序性：任一结点值均小于（或大于）它的所有后代结点值，最小值结点（或最大值结点）在堆的根上。
2. 结构性：堆总是一棵完全二叉树，即除了最底层，其他层的结点都被元素填满，且最底层尽可能地从左到右填入。

二叉树又是啥？请查看我的另一篇博文《心中有树——基础》

小根堆与大根堆
小根堆：结点值小于后代结点值的堆，也叫最小堆，图左
大根堆：结点值大于后代结点值的堆，也叫最大堆，图右

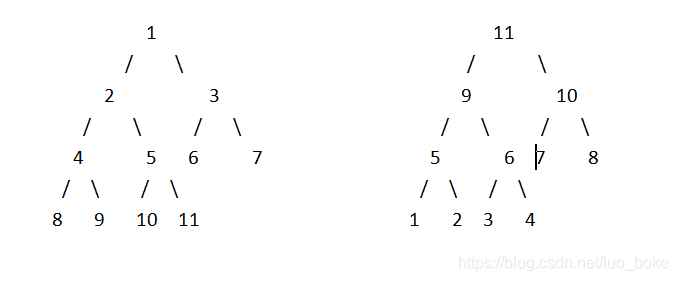
二叉堆
二叉堆是一种特殊的堆，即每个结点的子结点不超过2个。堆排序就是使用的二叉堆。

堆的存储
一般使用线性数据结构（如数组）存储堆：

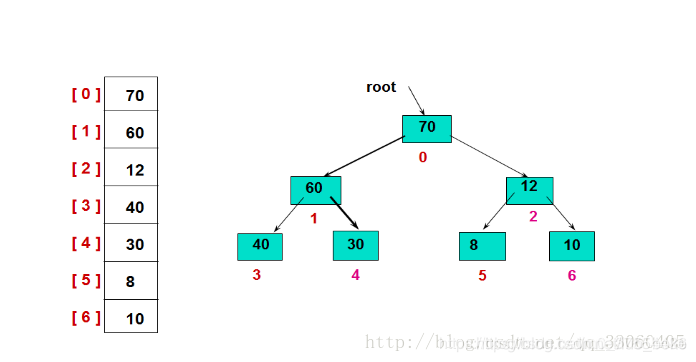
• 根结点存储在第0个位置
• 结点i的左孩子存储在2*i+1的位置
• 结点i的右孩子存储在2*i+2的位置

堆构建过程

1)根据子结点推父结点：（n-1）/2
2)根据父结点推子结点：左子结点（2n+1）,右子结点（2n+2）
索引由0开始计数

我们以9、12、5、24、0、1、99、3、10、7 这10个数来构建大根堆如下，

1. 首先我们将现在的无序序列看成一个堆结构，一个没有规则的二叉树，将序列里的值按照从上往下，从左到右依次填充到二叉树中。
   
2. 从最后一个叶子7遍历父结点，如果父<左右子结点最大值，则父结点值与最大子结点交换值。发现7和10都小于35，切换至99和3的父结点，发现99>24，交换24与99的位置。
   
3. 继续比较0和1的父结点，因0<5，1<5，往下走比较99和35的父结点，最大子结点99>12，交换位置。交换后，此时需要对12这个父结点进行排序，发现24>12,此时需要交换12和24的位置。
   
   
4. 继续对父结点9进行遍历操作，需要和99换位置，同理9需要最大的子结点35换位置。
   
5. 最终获得了大堆根
   
   构建代码

    /***
     * 构建大根堆
     * @param array  数据源
     */
    private void buildHeap(int[] array) {
        //从右向左，从下到上依次遍历父结点，建立大根堆，时间复杂度：O(n*log2n)
        for (int i = (array.length - 1 - 1) / 2; i >= 0; i--) {
            adjust(array, i, array.length - 1);
        }
    }
    
    /**
     * 将指定堆构建成大堆根函数
     * 逻辑
     * 1. 如果起始索引无子结点，则跳出该方法
     * 2. 如果只有一个左子结点，进行大小比较并置换值
     * 3. 如果有两个子结点，选择最大值与父结点比较,然后置换其位置。
     * 如果子结点大于父结点，置换完成后，递归进行同样操作，其子结点索引即是函数的start值
     *
     * @param array 源数组
     * @param start 起始索引
     * @param end   结尾索引
     */
    public void adjust(int[] array, int start, int end) {
        // 左子结点的位置
        int leftIndex = 2 * start + 1;
        if (leftIndex == end) {
            //只有一个左结点，进行比较并置换值
            if (array[leftIndex] > array[start]) {
                int temp = array[leftIndex];
                array[leftIndex] = array[start];
                array[start] = temp;
            }
        } else if (leftIndex < end) {
            //有两个子结点
            int temp = array[leftIndex];
            int tempIndex = leftIndex;
            if (array[leftIndex + 1] > array[leftIndex]) {
                temp = array[leftIndex + 1];
                tempIndex = leftIndex + 1;
            }
            if (temp > array[start]) {
                array[tempIndex] = array[start];
                array[start] = temp;
            }
            adjust(array, tempIndex, end);
        }
    }

堆排序过程

上面我们将大根堆构建好了，现在我们对堆进行排序。其构建思想是：

1. 根据堆的特点进行编写，先将一组拥有n个元素的数据构建成大根堆或者小根堆（我按照大根堆进行介绍，小根堆是一样的思想）。
2. 再将根结点上的数和堆最后一位数据进行互换，此时，第n位的数就是整个序列中最大的数。
3. 然后再将前n-1为元素进行构建形成大根堆，再将根结点与第n-1位数据进行互换，得到第二大数据，此时倒数两个数据无疑是有序的。
4. 然后将前n-2个数据构建成大根堆，依次循环直到剩下一位元素，则说明第一位后面的数字都是有序的，并且比第一位数大，此时排序完成。

• 1）将99和7替换，对排除99的堆进行重新构建大根堆
  
• 2）替换35和9的位置，对剩下的8个数进行重新构建大堆根
  
• 3）24与3交换位置，对剩余的7个数重新构建大根堆
  
• 4)后续过程同理，最终得到经过排序完成的堆 0、1、3、5、7、9、10、12、24、35、99
  

排序代码

    /**
     * 堆排序
     *
     * @param array 源数组
     */
    public void heapSort(int[] array) {
        buildHeap(array);
        int tmp;
        //要与root结点置换位置元素的索引
        int end = array.length - 1;
        //n个结点只用构建排序n-1次，最后只有1个元素不用在排序
        for (int i = array.length - 1; i > 0; i--) {
            tmp = array[0];
            array[0] = array[end];
            array[end] = tmp;

            end--;
            //头尾置换后，将堆重新构建为大堆根，置换尾部大元素不参加构建
            //因为除了root结点，其他都是由大到小有序的，所以再次构建大根堆时，不用在进行adjust()前的那个循环
            adjust(array, 0, end);
        }
    }

堆添加元素

添加元素时，新元素被添加到数组末尾，但是添加元素后，堆的性质可能会被破坏，需要向上调整堆结果。如给大堆根堆添加元素100。

此时此时堆的结构被破坏，需要从下往上进行调整。因100大于0，5,99，则新的大堆根为

元素添加代码

    /**
     * 在 array 是大堆根的前提下添加元素然后重构大堆根
     *
     * @param array 大堆根数组
     * @param value 添加的元素值
     */
    private void addHeap(int[] array, int value) {
        int[] arr = new int[array.length + 1];
        System.arraycopy(array, 0, arr, 0, array.length);
        arr[arr.length - 1] = value;
        int currentIndex = arr.length - 1;
        int parentIndex = (arr.length - 1) / 2;
        while (parentIndex >= 0) {
            if (value > arr[parentIndex]) {
                int temp = arr[parentIndex];
                arr[parentIndex] = value;
                arr[currentIndex] = temp;

                //如果最后一个元素的父结点还有父结点需要继续进行对比
                currentIndex = parentIndex;
                parentIndex = (currentIndex - 1) / 2;
            } else {
                break;
            }
        }
    }

堆删除元素

堆删除元素都是从结点删除，然后以这个结点为root结点的数组的最后一个元素移动到根结点的位置，并向下调整堆结构，直至重新符合堆序性。如我们删除结点35，将7移到35的位置

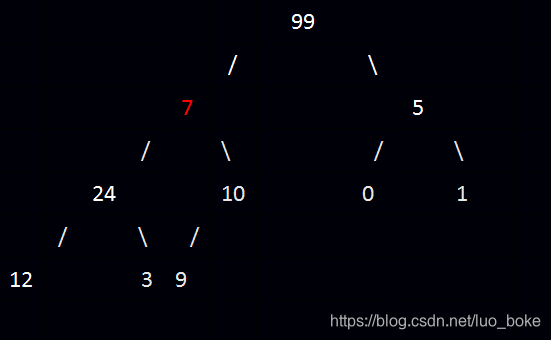
将7与其子结点逐个比较，直至符合大根堆规则

删除元素代码

/**
     * 在 array 是大堆根的前提下删除元素然后重构大堆根
     *
     * @param array 大堆根数组
     * @param deleteIndex 删除元素的索引
     */
    private int[] deleteHeap(int[] array, int deleteIndex) {
        array[deleteIndex] = array[array.length - 1];
        int[] arr = new int[array.length - 1];
        System.arraycopy(array, 0, arr, 0, array.length - 1);
        int lefeIndex = 2 * deleteIndex + 1;
        while (lefeIndex >= arr.length - 1) {
            int maxIndex = lefeIndex;
            if (arr.length - 1 > lefeIndex) {
                if (arr[lefeIndex + 1] > arr[lefeIndex]) {
                    maxIndex = lefeIndex + 1;
                }
            }

            if (arr[maxIndex] > arr[deleteIndex]) {
                int temp = arr[maxIndex];
                arr[maxIndex] = arr[deleteIndex];
                arr[deleteIndex] = temp;
                lefeIndex = 2 * maxIndex + 1;
            } else {
                break;
            }
        }
        return arr;
    }

Java中的堆

堆这块区域是JVM中最大的，应用的对象和数据都是存在这个区域，这块区域也是线程共享的，也是 gc 主要的回收区。一个 JVM 实例只存在一个堆类存，堆内存的大小是可以调节的。类加载器读取了类文件后，需要把类、方法、常变量放到堆内存中，以方便执行器执行，堆内存分为三部分：

新生区：是类的诞生、成长、消亡的区域，一个类在这里产生，应用，最后被垃圾回收器收集，结束生命。新生区又分为两部分：伊甸区（Eden space）和幸存者区（Survivor pace），所有的类都是在伊甸区被new出来的。

幸存区有两个：0区（Survivor 0 space）和1区（Survivor 1 space）。当伊甸园的空间用完时，程序又需要创建对象，JVM的垃圾回收器将对伊甸园进行垃圾回收（Minor GC）,将伊甸园中的剩余对象移动到幸存0区。

若幸存0区也满了，再对该区进行垃圾回收，然后移动到1区。那如果1去也满了呢？再移动到养老区。若养老区也满了，那么这个时候将产生Major GC（Full GC），进行养老区的内存清理。若养老区执行Full GC 之后发现依然无法进行对象的保存，就会产生OOM异常“OutOfMemoryError”。

出现java.lang.OutOfMemoryError: Java heap space异常，说明Java虚拟机的堆内存不够。原因有二：
1）Java虚拟机的堆内存设置不够，可以通过参数-Xms、-Xmx来调整。
2）代码中创建了大量大对象，并且长时间不能被垃圾收集器收集（存在被引用）。

养老区
用于保存从新生区筛选出来的 JAVA 对象，一般pool池对象都在这个区域活跃。

永久存储区
是一个常驻内存区域，用于存放JDK自身所携带的 Class,Interface 的元数据，也就是说它存储的是运行环境必须的类信息，被装载进此区域的数据是不会被垃圾回收器回收掉的，关闭 JVM 才会释放此区域所占用的内存。

如果出现java.lang.OutOfMemoryError: PermGen space，说明是Java虚拟机对永久代Perm内存设置不够。 原因有二：
1）程序启动需要加载大量的第三方jar包。例如：在一个Tomcat下部署了太多的应用。
2）大量动态反射生成的类不断被加载，最终导致Perm区被占满。

博客书写不易，您的点赞收藏是我前进的动力，千万别忘记点赞、 收**藏 ^ _ ^ !

相关链接

• 心中有树——基础
• 心中有栈
• 常见排序算法解析