acwing278(0/1背包)acwing278(0/1背包)acwing278(0/1背包)
(1)体积一定,求价值的最大或者最小价值
状态转移方程:f[i][j]=f[i−1][j]+f[i−1][j−v[i]]f[i][j] = f[i-1][j] + f[i-1][j-v[i]]f[i][j]=f[i−1][j]+f[i−1][j−v[i]] 不选择第i个数,选择第i个数
f[i]f[i]f[i] 每次出现的时候,没有被更新过,是f[i−1]f[i-1]f[i−1]
cin >> n >> m;
for(int i = 1; i <= n; i++) cin >> v[i];
f[0] = 1; // 和为0也是一种选法
for (int i = 1; i <= n; i++)
for (int j = m; j >= v[i]; j--)
f[j] += f[j - v[i]];
cout << f[m] << endl;
关于滚动数组:
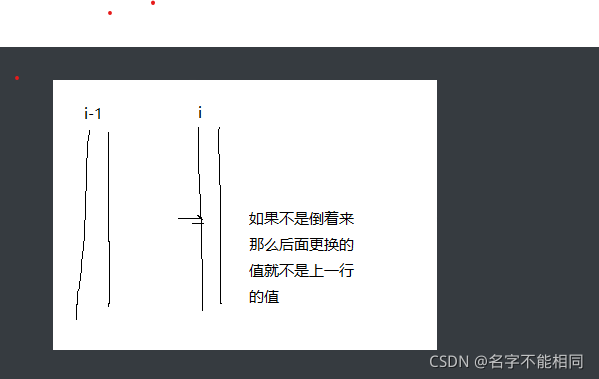




 这篇博客介绍了如何使用动态规划解决0/1背包问题,通过体积固定的物品选取,求解最大价值。状态转移方程为f[i][j]=f[i−1][j]+f[i−1][j−v[i]],并给出了滚动数组优化的实现代码。
这篇博客介绍了如何使用动态规划解决0/1背包问题,通过体积固定的物品选取,求解最大价值。状态转移方程为f[i][j]=f[i−1][j]+f[i−1][j−v[i]],并给出了滚动数组优化的实现代码。
















 1144
1144

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








