求路径最短时间(最喜欢的数学编程题)

提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档

---

题目

有一段路径，长度为y，汽车初速度为v，汽车可以在出发前花费时间改车，让初速度提升，提升的单位速度为x，求所需花费的最短时间

输入：整数v、x、y (v>=0， 1 <=x，y)
输出：小数，和最终结果差距小于10^(-6)即OK

---

题解

直接上公式(这里为了简便，设单位速度为a，初速度为b，路程为c，x为自变量，代表加速的时间)
f(x) = x + c / (ax + b)
这就是花费的总时间
然后就是硬求导，
f`(x) = 1 - ac / (ax + b)^2

展示下我帅气的草稿纸

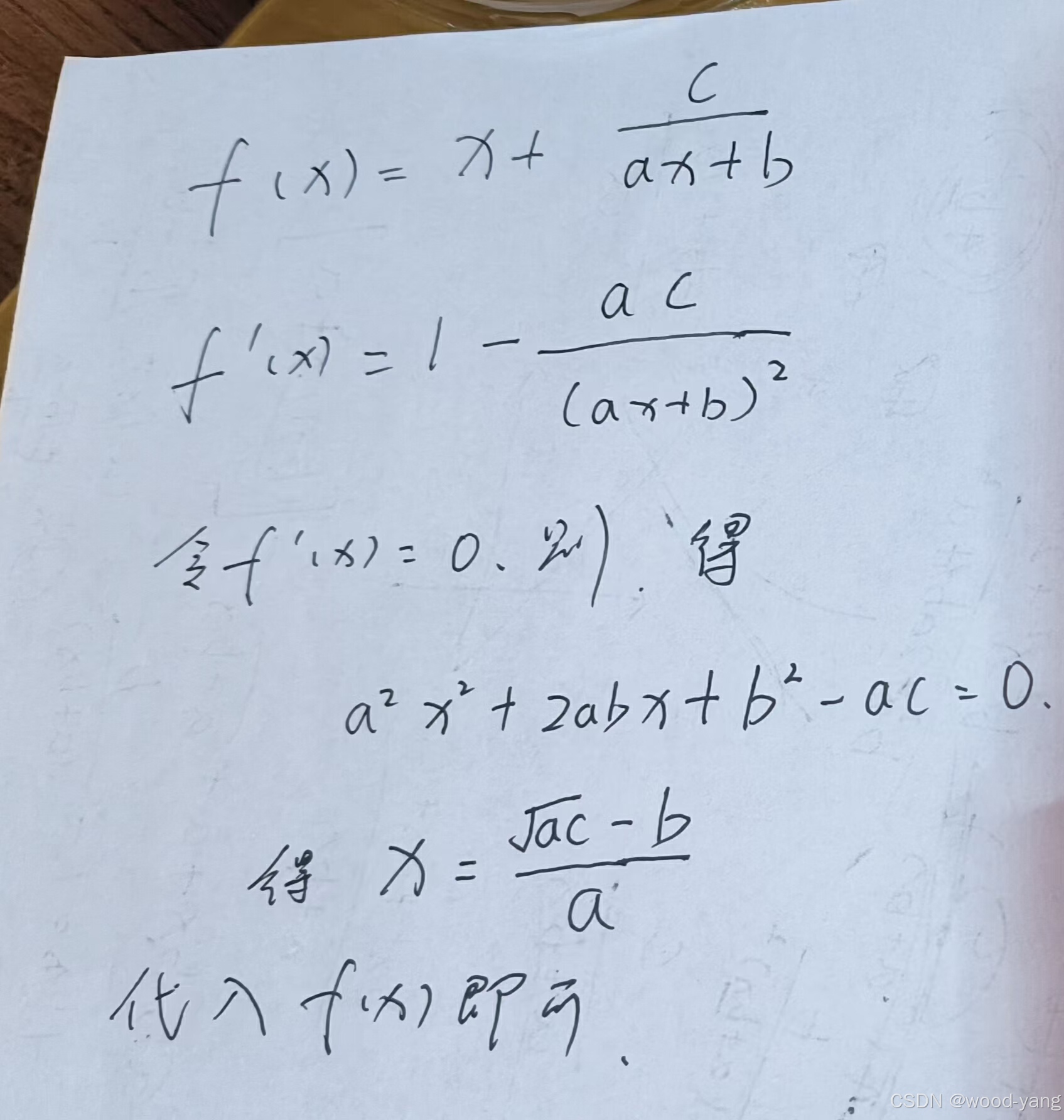
在来个代码

	public static void main(String[] args) {
        Scanner in = new Scanner(System.in);
        double v = in.nextInt();
        double x = in.nextInt();
        double y = in.nextInt();
        double ans = new Main().solve(v, x, y);
        System.out.printf("%.7f\n", ans);
    }

/*
0 1 2
 */
    private double solve(double v, double x, double y) {
        double t = (Math.sqrt(x * y) - v) / x;
        return t + y / (v + x * t);
    }

优化题解(推荐)

发现可以直接用对勾函数的结论，搞复杂了