2019牛客暑期多校训练营（第七场） Find the median（权值线段树+离散化）

题意+解题思路：

给你一种计算规则，让你计算出 L [ i ] , R [ i ] ，( i 取值是 1 - n )。然后每次增加 L[ i ] - R[ i ]  这些数，然后让你求当前的中位数，如果是偶数个（如 6 个 取第3个）。比如 L[ 1 ] = 5 , R [ 1 ] = 15 . 就会增加 5、6、7 ... ... 13、14、15 这些数。又因为区间大小为 1 - 10^9 比较大，但是 n 是4*10^5。所以可以开一个权值线段树来维护，不过需要对区间离散化来维护。有几个点说一下

举个例子： 有两个区间 [ 1, 10 ] 、[ 5，15 ] ,这时候维护的根节点的值应该什么呢？ 

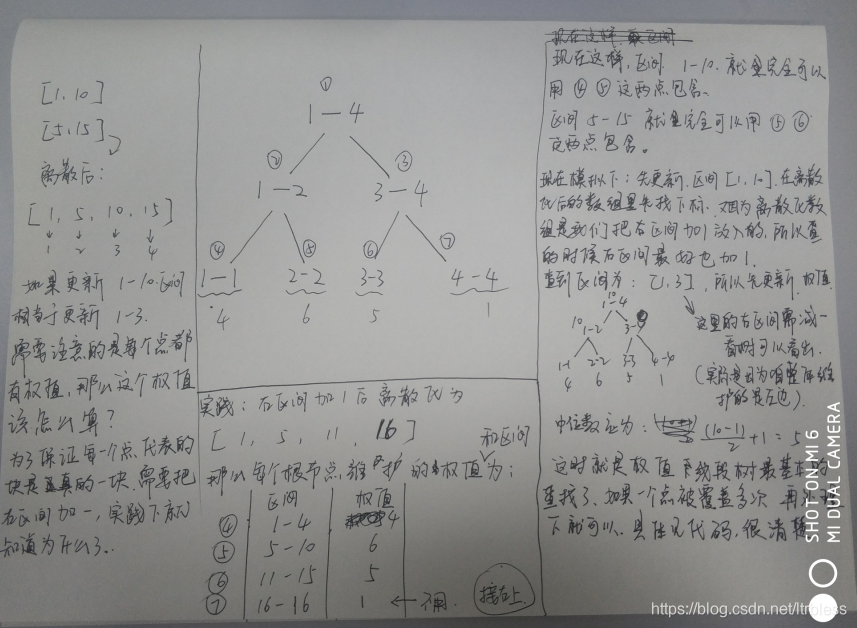
AC代码：

#include<bits/stdc++.h>
#define up(i, x, y) for(ll i = x; i <= y; i++)
#define down(i, x, y) for(ll i = x; i >= y; i--)
#define bug prllf("*********\n")
#define debug(x) cout<<#x"=["<<x<<"]" <<endl
#define IO ios::sync_with_stdio(false);cin.tie(0);cout.tie(0)
typedef long long ll;
typedef unsigned long long ull;
const double eps = 1e-8;
const ll mod = 1e9 + 7;
const ll maxn = 8e5 + 7;
const double pi = acos(-1);
const ll inf = 0x3f3f3f3f;
const ll INF = 0x3f3f3f3f3f3f3f3fLL;
using namespace std;

ll a[maxn];
ll n, x[maxn], y[maxn], a1, a2, b1,b2,c1,c2,m1,m2;
ll l[maxn], r[maxn];
ll cnt;
struct node
{
    ll l, r, f, v, sum; // v保存最初的基本权值  sum是更新区间后的真实权值  f是lazy标记
}t[maxn << 2];

void push_up(ll k)
{
    t[k].sum = t[k << 1].sum + t[k << 1 | 1].sum;
    t[k].v = t[k << 1].v + t[k << 1 | 1].v;
}

void push_down(ll k)
{
    t[k << 1].f += t[k].f; t[k << 1 | 1].f += t[k].f;
    t[k << 1].sum += t[k << 1].v * t[k].f;
    t[k << 1 | 1].sum += t[k << 1 | 1].v * t[k].f;
    t[k].f = 0;
}

void build(ll k, ll l, ll r)
{
    t[k].l = l, t[k].r = r;
    t[k].f = 0, t[k].sum = 0;
    if(l == r)
    {
        t[k].v = a[l + 1] - a[l]; // 基本权值
//        cout << k << ' ' << t[k].v << '\n';
        return ;
    }
    ll mid = (l + r) >> 1;
    build(k << 1, l, mid);
    build(k << 1 | 1, mid + 1, r);
    push_up(k);
}

void update(ll k, ll l, ll r)
{

    if(l <= t[k].l && t[k].r <= r)
    {
        t[k].sum += t[k].v; // 更新真实权值
        t[k].f++;
        return ;
    }
    if(t[k].f) push_down(k);
    ll mid = (t[k].l + t[k].r) >> 1;
    if(l <= mid) update(k << 1, l ,r);
    if(mid + 1 <= r) update(k << 1 | 1, l ,r);
    push_up(k);
}

void query(ll k, ll x, ll &ans)
{
    if(t[k].l == t[k].r)
    {
        ll time = t[k].sum / t[k].v; // 被覆盖过 time 次
        ll lll = a[ t[k].l ];
        ll pos = (x - 1) / time + 1; // 寻找中位数
        ans = lll + pos - 1; // 真实中位数大小
        return ;
    }

    if(t[k].f) push_down(k);

    if( t[k << 1].sum >= x ) query(k << 1, x, ans);

    else
    {
        query(k << 1 | 1, x - t[k << 1].sum, ans);
    }
    push_up(k);
}

ll getid(ll x)
{
    return lower_bound(a + 1, a + 1 + cnt, x) - a;
}

int main()
{
    cnt = 0;
    scanf("%lld", &n);
    scanf("%lld %lld %lld %lld %lld %lld", &x[1], &x[2], &a1, &b1, &c1, &m1);
    scanf("%lld %lld %lld %lld %lld %lld", &y[1], &y[2], &a2, &b2, &c2, &m2);
    for(ll i = 3; i <= n; i++)
    {
        x[i] = (a1 * x[i - 1] + b1 * x[i - 2] + c1) % m1;
        y[i] = (a2 * y[i - 1] + b2 * y[i - 2] + c2) % m2;
    }
    for(ll i = 1; i <= n; i++)
    {
        l[i] = min(x[i], y[i]) + 1;
        r[i] = max(x[i], y[i]) + 1;
        a[++cnt] = l[i];
        a[++cnt] = r[i] + 1;  // 右区间加一
//        cout << l[i] << ' ' << r[i] << '\n';
    }

//    l[1] = 1; l[2] = 5;
//    r[1] = 10; r[2] = 15;
//    a[1] = l[1]; a[2] = l[2]; a[3] = r[1] + 1; a[4] = r[2] +1;
//    cnt = 4;
//    n = 2;

    sort(a + 1, a + 1 + cnt);
    cnt = unique(a + 1, a + 1 + cnt) - a - 1;
//    debug(cnt);
    a[cnt + 1] = a[cnt] + 1; // 避免最右边根节点建树的时候数组越界
    build(1, 1 ,cnt);
    ll sum = 0;
    for(ll i = 1; i <= n; i++)
    {
        update(1, getid(l[i]), getid(r[i] + 1) - 1); // 更新区间
        ll ans = 0;
        sum += r[i] - l[i] + 1;  // 累计，计算需要查询第几个数
        query(1, (sum - 1) / 2 + 1, ans); // 查询并用ans，保留答案 （(sum - 1) / 2 + 1 --> 代表除2向上取整）
        printf("%lld\n", ans);
    }
}