【牛客】面试必刷TOP101——01链表

最新推荐文章于 2025-02-17 13:11:22 发布
最新推荐文章于 2025-02-17 13:11:22 发布
阅读量821 收藏
点赞数 1
分类专栏： 【刷题】刷题日记 文章标签： 算法 链表
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/lsz20000813/article/details/124307404
版权

BM1 反转链表

描述
给定一个单链表的头结点pHead(该头节点是有值的，比如在下图，它的val是1)，长度为n，反转该链表后，返回新链表的表头。

数据范围： 0≤n≤1000
要求：空间复杂度 O(1)，时间复杂度 O(n) 。

如当输入链表{1,2,3}时，
经反转后，原链表变为{3,2,1}，所以对应的输出为{3,2,1}。
以上转换过程如下图所示：
在这里插入图片描述

示例1
输入：{1,2,3}
返回值：{3,2,1}

示例2
输入：{}
返回值：{}
说明：
空链表则输出空

我的思路：
初始化：3个指针
1）pre指针指向已经反转好的链表的最后一个节点，最开始没有反转，所以指向nullptr
2）cur指针指向待反转链表的第一个节点，最开始第一个节点待反转，所以指向head
3）nex指针指向待反转链表的第二个节点，目的是保存链表，因为cur改变指向后，后面的链表则失效了，所以需要保存
接下来，循环执行以下三个操作
1）nex = cur->next, 保存作用
2）cur->next = pre 未反转链表的第一个节点的下个指针指向已反转链表的最后一个节点
3）pre = cur， cur = nex; 指针后移，操作下一个未反转链表的第一个节点
循环条件，当然是cur != nullptr
循环结束后，cur当然为nullptr，所以返回pre，即为反转后的头结点
如图所示：
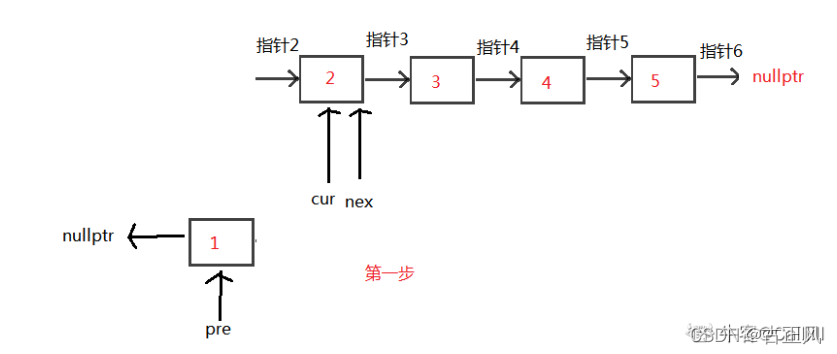
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
以此类推。

代码如下：

/*
struct ListNode {
	int val;
	struct ListNode *next;
	ListNode(int x) :
			val(x), next(NULL) {
	}
};*/
class Solution {
public:
    ListNode* ReverseList(ListNode* pHead) {
        ListNode* next=nullptr;
        ListNode* pre=nullptr;
        ListNode* cur=pHead;
        
        while(cur!=nullptr)
        {
            next=cur->next;
            cur->next=pre;
            pre=cur;
            cur=next;
        }
        return pre;
    }
};

BM2 链表内指定区间反转

描述
将一个节点数为 size 链表 m 位置到 n 位置之间的区间反转，要求时间复杂度 O(n)，空间复杂度 O(1)。
例如：
给出的链表为 1→2→3→4→5→NULL, m=2,n=4
返回 1→4→3→2→5→NULL.

数据范围： 链表长度 0<size≤1000，0<m≤n≤size，链表中每个节点的值满足 ∣val∣≤1000
要求：时间复杂度 O(n) ，空间复杂度 O(n)
进阶：时间复杂度 O(n)，空间复杂度 O(1)

示例1
输入：{1,2,3,4,5},2,4
返回值：{1,4,3,2,5}

示例2
输入：{5},1,1
返回值：{5}

我的思路：
方法一：栈
把待旋转的地方先存在栈里，再依次出栈。

/**
 * struct ListNode {
 *	int val;
 *	struct ListNode *next;
 * };
 */

class Solution {
public:
    /**
     * 
     * @param head ListNode类 
     * @param m int整型 
     * @param n int整型 
     * @return ListNode类
     */
    ListNode* reverseBetween(ListNode* head, int m, int n) {
        // write code here
        if(head==nullptr||m==n){
            return head;
        }
        //方法一：
        stack<int> stk;
        ListNode* p=head;
        int i=1;
        while(i<m)
        {
            p=p->next;
            i++;
        }
        ListNode* q=p;
        while(i<=n)
        {
            stk.push(p->val);
            p=p->next;
            i++;
        }
        p=q;
        while(!stk.empty()){
            p->val=stk.top();
            stk.pop();
            p=p->next;
        }
        return head;

方法二：三指针
在这里插入图片描述

/**
 * struct ListNode {
 *	int val;
 *	struct ListNode *next;
 * };
 */

class Solution {
public:
    /**
     * 
     * @param head ListNode类 
     * @param m int整型 
     * @param n int整型 
     * @return ListNode类
     */
    ListNode* reverseBetween(ListNode* head, int m, int n) {
        // write code here
        if(head==nullptr||m==n){
            return head;
        }
        //方法二
        ListNode* head_node =new ListNode(-1);
        head_node->next=head;
        ListNode* begin=head_node;
        int i=0;
        while(i<m-1)
        {
            begin=begin->next;
            i++;
        }
        ListNode* start=begin->next;
        ListNode* finish=begin;
        while(i<n)
        {
            finish=finish->next;
            i++;
        }
        ListNode* end=finish->next;
        
        ListNode* p=start;
        ListNode* q=p->next;
        begin->next=nullptr;
        finish->next=nullptr; 
        while(p!=finish){
            ListNode* tmp=q->next;
            q->next=p;
            p=q;
            q=tmp;
        }
        begin->next=finish;
        start->next=end;
        head=head_node->next;
        delete head_node;
        return head;
    }

BM3 链表中的节点每k个一组翻转

描述
将给出的链表中的节点每 k 个一组翻转，返回翻转后的链表
如果链表中的节点数不是 k 的倍数，将最后剩下的节点保持原样
你不能更改节点中的值，只能更改节点本身。

数据范围： 0≤n≤2000 ，1≤k≤2000 ，链表中每个元素都满足 0≤val≤1000
要求空间复杂度 O(1)，时间复杂度 O(n)
例如：
给定的链表是 1→2→3→4→5
对于 k = 2k=2 , 你应该返回 2→1→4→3→5
对于 k = 3k=3 , 你应该返回 3→2→1→4→5

示例1
输入：{1,2,3,4,5},2
返回值：{2,1,4,3,5}

示例2
输入：{},1
返回值：{}

我的思路：
在这里插入图片描述
代码如下：

/**
 * struct ListNode {
 *	int val;
 *	struct ListNode *next;
 * };
 */

class Solution {
public:
    /**
     * 
     * @param head ListNode类 
     * @param k int整型 
     * @return ListNode类
     */
    ListNode* reverseKGroup(ListNode* head, int k) {
        // write code here
        if(head==nullptr) return head;
        int len=0;
        for(ListNode* p=head;p;p=p->next)
        {
            len++;
        }
        int cnt=len/k;
        ListNode* h=new ListNode(0);
        h->next=head;
        ListNode* r=h;
        ListNode* p=head;
        ListNode* q=p->next;
        ListNode *s,*t;
        while(cnt--)
        {
            s=p;
            for(int i=0;i<k-1;i++)
            {
                t=q->next;
                q->next=p;
                p=q;
                q=t;
            }
            r->next=p;
            s->next=q;
            
            r=s;
            p=q;
            q=p->next;
        }
        return h->next;
    }
};

BM4 合并两个排序的链表

描述
输入两个递增的链表，单个链表的长度为n，合并这两个链表并使新链表中的节点仍然是递增排序的。
数据范围： 0 \le n \le 10000≤n≤1000，-1000 \le 节点值 \le 1000−1000≤节点值≤1000
要求：空间复杂度 O(1)O(1)，时间复杂度 O(n)O(n)

如输入{1,3,5},{2,4,6}时，合并后的链表为{1,2,3,4,5,6}，所以对应的输出为{1,2,3,4,5,6}，转换过程如下图所示：
在这里插入图片描述

或输入{-1,2,4},{1,3,4}时，合并后的链表为{-1,1,2,3,4,4}，所以对应的输出为{-1,1,2,3,4,4}，转换过程如下图所示：
在这里插入图片描述

示例1
输入：{1,3,5},{2,4,6}
返回值：{1,2,3,4,5,6}

示例2
输入：{},{}
返回值：{}

示例3
输入：{-1,2,4},{1,3,4}
返回值：{-1,1,2,3,4,4}

我的思路：
方法一：递归

/*
struct ListNode {
	int val;
	struct ListNode *next;
	ListNode(int x) :
			val(x), next(NULL) {
	}
};*/
class Solution {
public:
    ListNode* Merge(ListNode* pHead1, ListNode* pHead2) {
        if(pHead1==nullptr) return pHead2;
        if(pHead2==nullptr) return pHead1;
        
        if(pHead1->val<=pHead2->val)
        {
            pHead1->next=Merge(pHead1->next, pHead2);
            return pHead1;
        }
        else
        {
            pHead2->next=Merge(pHead2->next, pHead1);
            return pHead2;
        }
    }
};

方法二：非递归　模拟

/*
struct ListNode {
	int val;
	struct ListNode *next;
	ListNode(int x) :
			val(x), next(NULL) {
	}
};*/
class Solution {
public:
    ListNode* Merge(ListNode* pHead1, ListNode* pHead2) {
        if(pHead1==nullptr) return pHead2;
        if(pHead2==nullptr) return pHead1;
        ListNode* h=new ListNode(0);
        ListNode* head=h;
        while(pHead1 && pHead2)
        {
            if(pHead1->val<=pHead2->val)
            {
                h->next=pHead1;
                h=h->next;
                pHead1=pHead1->next;
            }
            else
            {
                h->next=pHead2;
                h=h->next;
                pHead2=pHead2->next;
            }
        }
        if(pHead1)
            h->next=pHead1;
        else
            h->next=pHead2;
        return head->next;
    }
};

BM5 合并k个已排序的链表

描述
合并 k 个升序的链表并将结果作为一个升序的链表返回其头节点。

数据范围：节点总数满足 0≤n≤10^5
，链表个数满足 1≤k≤10^5 ，
每个链表的长度满足1≤len≤200 ，
每个节点的值满足 ∣val∣<=1000
要求：时间复杂度O(nlogk)

示例1
输入：[{1,2,3},{4,5,6,7}]
返回值：{1,2,3,4,5,6,7}

示例2
输入：[{1,2},{1,4,5},{6}]
返回值：{1,1,2,4,5,6}

我的思路：优先队列
先把所有数据存放在递增的优先队列中，依次出队。

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *mergeKLists(vector<ListNode *> &lists) {
        priority_queue<int,vector<int>,greater<int>> q;
        for(int i=0;i<lists.size();i++)
        {
             ListNode* h=lists[i];
            while(h)
            {
                q.push(h->val);
                h=h->next;
            }
        }
        ListNode* head=new ListNode(0);
        ListNode* p=head;
        while(!q.empty())
        {
            p->next=new ListNode(q.top());
            q.pop();
            p=p->next;
        }
        return head->next;
    }
};

BM6 判断链表中是否有环

描述
判断给定的链表中是否有环。如果有环则返回true，否则返回false。
数据范围：链表长度 0 \le n \le 100000≤n≤10000，链表中任意节点的值满足 ∣val∣<=100000
要求：空间复杂度 O(1)，时间复杂度 O(n)

输入分为两部分，第一部分为链表，第二部分代表是否有环，然后将组成的head头结点传入到函数里面。-1代表无环，其它的数字代表有环，这些参数解释仅仅是为了方便读者自测调试。实际在编程时读入的是链表的头节点。

例如输入{3,2,0,-4},1时，对应的链表结构如下图所示：
在这里插入图片描述
可以看出环的入口结点为从头结点开始的第1个结点（注：头结点为第0个结点），所以输出true。

示例1
输入：{3,2,0,-4},1
返回值：true
说明：
第一部分{3,2,0,-4}代表一个链表，第二部分的1表示，-4到位置1（注：头结点为位置0），即-4->2存在一个链接，组成传入的head为一个带环的链表，返回true

示例2
输入：{1},-1
返回值：false
说明：
第一部分{1}代表一个链表，-1代表无环，组成传入head为一个无环的单链表，返回false

示例3
输入：{-1,-7,7,-4,19,6,-9,-5,-2,-5},6
返回值：true

我的思路：双指针
快慢指针，快指针一次走两步，慢指针一次走一步，如果有环一定会有相等的时候。

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    bool hasCycle(ListNode *head) {
        if(!head) return false;
        ListNode* p=head;
        ListNode* q=head;
        while(q&&q->next)
        {
            p=p->next;
            q=q->next->next;
            if(p==q) return true;
        }
        return false;
    }
};

BM7 链表中环的入口结点

描述
给一个长度为n链表，若其中包含环，请找出该链表的环的入口结点，否则，返回null。

数据范围：n≤10000，1<=结点值<=10000
要求：空间复杂度 O(1)，时间复杂度 O(n)

例如，输入{1,2},{3,4,5}时，对应的环形链表如下图所示：
在这里插入图片描述

可以看到环的入口结点的结点值为3，所以返回结点值为3的结点。
输入描述：
输入分为2段，第一段是入环前的链表部分，第二段是链表环的部分，后台会根据第二段是否为空将这两段组装成一个无环或者有环单链表
返回值描述：
返回链表的环的入口结点即可，我们后台程序会打印这个结点对应的结点值；若没有，则返回对应编程语言的空结点即可。

示例1
输入：{1,2},{3,4,5}
返回值：3
说明：返回环形链表入口结点，我们后台程序会打印该环形链表入口结点对应的结点值，即3

示例2
输入：{1},{}
返回值：“null”
说明：没有环，返回对应编程语言的空结点，后台程序会打印"null"

示例3
输入：{},{2}
返回值：2
说明：环的部分只有一个结点，所以返回该环形链表入口结点，后台程序打印该结点对应的结点值，即2

我的思路：
方法一：哈希法
遍历链表，把每个节点判断是否存在set里。如果不存在，把节点放入set，如果存在，就直接返回。

/*
struct ListNode {
    int val;
    struct ListNode *next;
    ListNode(int x) :
        val(x), next(NULL) {
    }
};
*/
class Solution {
public:
    ListNode* EntryNodeOfLoop(ListNode* pHead) {
        //方法一：set
        unordered_set<ListNode*> set;
        ListNode* cur=pHead;
        while(cur)
        {
            if(set.count(cur)){
                return cur;
            }else{
                set.insert(cur);
            }
            cur=cur->next;
        }
        return nullptr;
    }
};

方法二：双指针
类似于BM6，快慢指针找到交点之后，把其中一个指针放置在链表开头，然后两个指针依次走一步，再次相交即是入环节点。
在这里插入图片描述

/*
struct ListNode {
    int val;
    struct ListNode *next;
    ListNode(int x) :
        val(x), next(NULL) {
    }
};
*/
class Solution {
public:
    ListNode* EntryNodeOfLoop(ListNode* pHead) {
        //方法一：快慢指针
        if(!pHead) return nullptr;
        ListNode* p=pHead;
        ListNode* q=pHead;
        
        while(q&&q->next)
        {
            q=q->next->next;
            p=p->next;
            if(p==q)
            {
                q=pHead;
                while(p!=q)
                {
                    p=p->next;
                    q=q->next;
                }
                return p;
            }
        }
        return nullptr;
    }
}；

BM8 链表中倒数最后k个结点

描述
输入一个长度为 n 的链表，设链表中的元素的值为 ai ，返回该链表中倒数第k个节点。
如果该链表长度小于k，请返回一个长度为 0 的链表。

数据范围：0≤n≤10^5
，0≤ ai ≤10 ^9
，0≤k≤10 ^9

要求：空间复杂度 O(n)，时间复杂度 O(n)
进阶：空间复杂度 O(1)，时间复杂度 O(n)

例如输入{1,2,3,4,5},2时，对应的链表结构如下图所示：
在这里插入图片描述
其中蓝色部分为该链表的最后2个结点，所以返回倒数第2个结点（也即结点值为4的结点）即可，系统会打印后面所有的节点来比较。

示例1
输入：{1,2,3,4,5},2
返回值：{4,5}
说明：返回倒数第2个节点4，系统会打印后面所有的节点来比较。

示例2
输入：{2},8
返回值：{}

我的思路：双指针
快慢指针，快指针先走K步，然后快慢指针依次走一步，直到快指针为nullptr，返回慢指针。

/**
 * struct ListNode {
 *	int val;
 *	struct ListNode *next;
 *	ListNode(int x) : val(x), next(nullptr) {}
 * };
 */
class Solution {
public:
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param pHead ListNode类 
     * @param k int整型 
     * @return ListNode类
     */
    ListNode* FindKthToTail(ListNode* pHead, int k) {
        // write code here
        ListNode* p=pHead;
        ListNode* q=pHead;   
        while(k-->0) 
        {
            if(!q) return nullptr;
            q=q->next;
        }
        while(q)
        {
            p=p->next;
            q=q->next;
        }
        return p;       
    }
};

BM9 删除链表的倒数第n个节点

描述
给定一个链表，删除链表的倒数第 n 个节点并返回链表的头指针
例如，
给出的链表为: 1→2→3→4→5, n=2.
删除了链表的倒数第 n 个节点之后,链表变为1→2→3→5.

数据范围： 链表长度 0≤n≤1000，链表中任意节点的值满足 0≤val≤100
要求：空间复杂度 O(1)，时间复杂度 O(n)
备注：题目保证 n 一定是有效的

示例1
输入：{1,2},2
返回值：{2}

我的思路：双指针
和BM8类似，快慢指针快指针先走k步，然后快慢指针依次走一步，直到快指针为nullptr。然后慢指针的next=next->next，这样就可以直接删除掉。

/**
 * struct ListNode {
 *	int val;
 *	struct ListNode *next;
 * };
 */

class Solution {
public:
    /**
     * 
     * @param head ListNode类 
     * @param n int整型 
     * @return ListNode类
     */
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        // write code here
        if(!head) return head;
        ListNode* p=head;
        ListNode* q=head;
        for(int i =0;i<n;i++)
        {
            q=q->next;
        }
        if(!q) return head->next;
        while(q->next)
        {
            p=p->next;
            q=q->next;
        }
        p->next=p->next->next;
        return head;
    }
};

BM10 两个链表的第一个公共结点

描述
输入两个无环的单向链表，找出它们的第一个公共结点，如果没有公共节点则返回空。（注意因为传入数据是链表，所以错误测试数据的提示是用其他方式显示的，保证传入数据是正确的）

数据范围：n≤1000
要求：空间复杂度O(1)，时间复杂度 O(n)

例如，输入{1,2,3},{4,5},{6,7}时，两个无环的单向链表的结构如下图所示：
在这里插入图片描述

可以看到它们的第一个公共结点的结点值为6，所以返回结点值为6的结点。
输入描述：
输入分为是3段，第一段是第一个链表的非公共部分，第二段是第二个链表的非公共部分，第三段是第一个链表和第二个链表的公共部分。 后台会将这3个参数组装为两个链表，并将这两个链表对应的头节点传入到函数FindFirstCommonNode里面，用户得到的输入只有pHead1和pHead2。
返回值描述：
返回传入的pHead1和pHead2的第一个公共结点，后台会打印以该节点为头节点的链表。

示例1
输入：{1,2,3},{4,5},{6,7}
返回值：{6,7}
说明：第一个参数{1,2,3}代表是第一个链表非公共部分，第二个参数{4,5}代表是第二个链表非公共部分，最后的{6,7}表示的是2个链表的公共部分这3个参数最后在后台会组装成为2个两个无环的单链表，且是有公共节点的

示例2
输入：{1},{2,3},{}
返回值：{}
说明：2个链表没有公共节点 ,返回null，后台打印{}

我的思路：合并链表
这里先假设链表A头结点与结点8的长度 与 链表B头结点与结点8的长度相等，那么就可以用双指针
初始化：指针ta指向链表A头结点，指针tb指向链表B头结点
如果ta== tb， 说明找到了第一个公共的头结点，直接返回即可。
否则，ta != tb，则++ta，++tb
所以现在的问题就变成，如何让本来长度不相等的变为相等的？
假设链表A长度为a， 链表B的长度为b，此时a != b
但是，a+b == b+a
因此，可以让a+b作为链表A的新长度，b+a作为链表B的新长度。
如图：
在这里插入图片描述

/*
struct ListNode {
	int val;
	struct ListNode *next;
	ListNode(int x) :
			val(x), next(NULL) {
	}
};*/
class Solution {
public:
    ListNode* FindFirstCommonNode( ListNode* pHead1, ListNode* pHead2) {
        ListNode* p1=pHead1;
        ListNode* p2=pHead2;
        while(p1!=p2)
        {
            p1 = p1?p1->next:pHead2;
            p2 = p2?p2->next:pHead1;
        }
        return p1;
    }
};

BM11 链表相加(二)

描述
假设链表中每一个节点的值都在 0 - 9 之间，那么链表整体就可以代表一个整数。
给定两个这种链表，请生成代表两个整数相加值的结果链表。
数据范围：0 \le n,m \le 10000000≤n,m≤1000000，链表任意值 0 \le val \le 90≤val≤9
要求：空间复杂度 O(n)O(n)，时间复杂度 O(n)O(n)

例如：链表 1 为 9->3->7，链表 2 为 6->3，最后生成新的结果链表为 1->0->0->0。
在这里插入图片描述

示例1
输入：[9,3,7],[6,3]
返回值：{1,0,0,0}
说明：如题面解释

示例2
输入：[0],[6,3]
返回值：{6,3}

我的思路：反转链表
先把两个链表反转，在依次相加，合成新链表后再反转。

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */

class Solution {
public:
    /**
     * 
     * @param head1 ListNode类 
     * @param head2 ListNode类 
     * @return ListNode类
     */
    ListNode *reverseList(ListNode *head) {
        if (head == nullptr || head->next == nullptr) return head;
        ListNode *l = head, *r = l->next;
        l->next = nullptr;
        while (r) {
            ListNode *t = r->next;
            r->next = l;
            l = r;
            r = t;
        }
        return l;
    }
    ListNode* addInList(ListNode* head1, ListNode* head2) {
        // write code here
        if(!head1) return head2;
        if(!head2) return head1;
        ListNode* l1=reverseList(head1);
        ListNode* l2=reverseList(head2);
        int carry=0;
        ListNode* ans=new ListNode(0),*cur=ans;
        while(l1||l2||carry)
        {
            int x = l1?l1->val:0;
            int y = l2?l2->val:0;
            int sum = x+y+carry;
            carry=sum/10;
            sum %= 10;
            cur->next = new ListNode(sum);
            cur =cur->next;
            if(l1) l1=l1->next;
            if(l2) l2=l2->next;
        }
        ans =ans->next;
        ans=reverseList(ans);
        return ans;
    }
};

BM12 单链表的排序

描述
给定一个节点数为n的无序单链表，对其按升序排序。

数据范围：0<n≤100000
要求：时间复杂度 O(nlogn)

示例1
输入：{1,3,2,4,5}
返回值：{1,2,3,4,5}

示例2
输入：{-1,0,-2}
返回值：{-2,-1,0}

我的思路：模拟
遍历链表，把所有的元素存放在vector里面，在vector进行排序后，依次输入到新链表里。

/**
 * struct ListNode {
 *	int val;
 *	struct ListNode *next;
 * };
 */

class Solution {
public:
    /**
     * 
     * @param head ListNode类 the head node
     * @return ListNode类
     */
    ListNode* sortInList(ListNode* head) {
        // write code here
        vector<int> v;
        while(head)
        {
            v.push_back(head->val);
            head = head->next;
        }
        sort(v.begin(),v.end());
        ListNode* ans=new ListNode(0),*cur = ans;
        for(int i:v)
        {
            cur->next=new ListNode(i);
            cur=cur->next;
        }
        return ans->next;
    }
};

BM13 判断一个链表是否为回文结构

描述
给定一个链表，请判断该链表是否为回文结构。
回文是指该字符串正序逆序完全一致。
数据范围： 链表节点数 0≤n≤10 ^5
，链表中每个节点的值满足 ∣val∣≤10 ^7

示例1
输入：{1}
返回值：true

示例2
输入：{2,1}
返回值：false
说明：2->1

示例3
输入：{1,2,2,1}
返回值：true
说明：1->2->2->1

我的思路：
方法一：字符串
在遍历链表的同时，分别采用头插和尾插的方法构造2个字符串，然后比较这两个字符串是否相等即可。

/**
 * struct ListNode {
 *	int val;
 *	struct ListNode *next;
 * };
 */

class Solution {
public:
    /**
     * 
     * @param head ListNode类 the head
     * @return bool布尔型
     */
    bool isPail(ListNode* head) {
        // write code here
        //方法一：
        ListNode* p=head;
        string s1,s2;
        bool ret=true;
        while(p)
        {
            s1+=(char)p->val;
            s2=(char)p->val+s2;
            p=p->next;
        }
        return s1==s2;
    }
};

方法二：双指针
双指针找中点，快指针走两步，慢指针走一步，快指针指向nullptr时，慢指针指向中间，再
把后半段反转。再依次遍历两个指针，判断元素是否相同即可。

/**
 * struct ListNode {
 *	int val;
 *	struct ListNode *next;
 * };
 */

class Solution {
public:
    /**
     * 
     * @param head ListNode类 the head
     * @return bool布尔型
     */
    ListNode* reverseList(ListNode* head){
        if(!head || !head->next) return head;
        ListNode* cur=head;
        ListNode* p=nullptr;
        while(cur)
        {
            ListNode* tmp=cur->next;
            cur->next=p;
            p=cur;
            cur=tmp;
        }
        return p;        
    }
    bool isPail(ListNode* head) {
        // write code here
        //方法二：
        if(!head || !head->next) return true;
        ListNode* p=head;
        ListNode* q =head;
        while(q&&q->next)
        {
            q=q->next->next;
            p=p->next;
        }
        ListNode* mid=(!q)?p:p->next;
        ListNode* end=reverseList(mid);
        while(end)
        {
            if(end->val!=head->val) return false;
            end=end->next;
            head=head->next;
        }
        return true;
    }
};

BM14 链表的奇偶重排

描述
给定一个单链表，请设定一个函数，将链表的奇数位节点和偶数位节点分别放在一起，重排后输出。
注意是节点的编号而非节点的数值。

数据范围：节点数量满足 0≤n≤10^5 ，节点中的值都满足0≤val≤1000
要求：空间复杂度 O(n)，时间复杂度 O(n)

示例1
输入：{1,2,3,4,5,6}
返回值:{1,3,5,2,4,6}
说明：1->2->3->4->5->6->NULL
重排后为1->3->5->2->4->6->NULL

示例2
输入：{1,4,6,3,7}
返回值：{1,6,7,4,3}
说明：1->4->6->3->7->NULL
重排后为1->6->7->4->3->NULL
奇数位节点有1,6,7，偶数位节点有4,3。重排后为1,6,7,4,3

备注：
链表长度不大于200000。每个数范围均在int内。

我的思路：利用链表操作，一次遍历即可（常数空间的解法）
我们定义两个头部节点odd和even, 分别表示“奇链表”和“偶链表”的头结点，每遍历一次，往对应链表尾部插入一个节点，最后“奇链表”的尾部指向“偶链表”的头部即可。
在这里插入图片描述

/**
 * struct ListNode {
 *	int val;
 *	struct ListNode *next;
 *	ListNode(int x) : val(x), next(nullptr) {}
 * };
 */
class Solution {
public:
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param head ListNode类 
     * @return ListNode类
     */
    ListNode* oddEvenList(ListNode* head) {
        // write code here
        if(!head) return head;
        ListNode* odd=head;
        ListNode* even=head->next;
        ListNode* evenhead=even;
        while(even && even->next)
        {
            odd->next=even->next;
            odd=odd->next;
            even->next=odd->next;
            even=even->next;
        }
        odd->next=evenhead;
        return head;
    }
};

BM15 删除有序链表中重复的元素-I

描述
删除给出链表中的重复元素（链表中元素从小到大有序），使链表中的所有元素都只出现一次
例如：
给出的链表为1→1→2,返回1→2.
给出的链表为1→1→2→3→3,返回1→2→3.

数据范围：链表长度满足 0≤n≤100，链表中任意节点的值满足 ∣val∣≤100
进阶：空间复杂度 O(1)，时间复杂度 O(n)

示例1
输入：{1,1,2}
返回值：{1,2}

示例2
输入：{}
返回值：{}

我的思路：一次遍历
如果该元素和下一个元素相同，就直接跳过。

/**
 * struct ListNode {
 *	int val;
 *	struct ListNode *next;
 * };
 */

class Solution {
public:
    /**
     * 
     * @param head ListNode类 
     * @return ListNode类
     */
    ListNode* deleteDuplicates(ListNode* head) {
        // write code here
        if(!head) return head;
        ListNode* p = head;
        while(p&&p->next)
        {
            if(p->val==p->next->val)
            {
                p->next=p->next->next;
            }else{
                p=p->next;
            }
        }
        return head;
    }
};

BM16 删除有序链表中重复的元素-II

描述
给出一个升序排序的链表，删除链表中的所有重复出现的元素，只保留原链表中只出现一次的元素。
例如：
给出的链表为1→2→3→3→4→4→5, 返回1→2→5.
给出的链表为1→1→1→2→3, 返回2→3.

数据范围：链表长度 0≤n≤10000，链表中的值满足 ∣val∣≤1000
要求：空间复杂度 O(n)，时间复杂度 O(n)
进阶：空间复杂度 O(1)，时间复杂度 O(n)

示例1
输入：{1,2,2}
返回值：{1}

示例2
输入：{}
返回值：{}

我的思路：双指针
快指针q探测并跳过重复的节点，慢指针p指向已检查过的最后一个，使用p->next = q删除重复的节点
难点：头节点也可能要删除。这里往头部之前加一个虚拟头部h，让p先指向h

/**
 * struct ListNode {
 *	int val;
 *	struct ListNode *next;
 * };
 */

class Solution {
public:
    /**
     * 
     * @param head ListNode类 
     * @return ListNode类
     */
    ListNode* deleteDuplicates(ListNode* head) {
        // write code here
        if(!head) return head;
        ListNode* h=new ListNode(0);
        h->next=head;
        ListNode* p=h;
        ListNode* q=head;
        while(q && q->next)
        {
            if(q->val!=q->next->val)
            {
                p=q;
                q=q->next;
            }
            else
            {
                int tmp=q->val;
                while(q&&q->val==tmp)
                {
                    q=q->next;
                }
                p->next=q;
            }
        }
        return h->next;
    }
};
2025华为OD面试手撕代码真题目录
MISAYAONE的博客
04-28 7万+
一般面试的时候每一轮技术面都会出一到两个手撕代码题，这些题的特点就是，非常短小，易于理解。不可能会再出阅读理解一样的机试题的。但是这些题目也非常注意基本功，很注意细节的处理，一般都是easy+medium题目。但是大家一定要注意，因为大部分面试官上面一开始就会让你做题，直接看你所有的做题过程（防止有人水平一般，机试就网上找的答案的蒙混过关），手撕代码题会给你后面的面试定一个基调。
Java面试八股文（素材来自网络）
热门推荐
weixin_50776418的博客
07-14 1万+
不定时更新，素材来自网络，都附注有超链接，侵删 联系邮箱：zhenyu_li1998@163.com
【牛客网面试必刷TOP101】二叉树篇（三）
qq_66314292的博客
09-01 2190
二叉树是数据结构中重要的一个章节，他的重要性也不言而喻，在未来不管是笔试还是面试都会遇到这类的题目，所以接下来我就会把一些常考的题目全部整理出来供大家学习指正。
【刷题笔记】之牛客面试必刷TOP101（1）
m0_58761900的博客
08-23 1889
1. 反转链表（双链表头插法 / 栈） 2.链表内指定区间反转 3. 链表中的节点每k个一组翻转 4. 合并两个排序的链表 5. 合并k个已排序的链表
牛客网算法篇之面试必刷TOP101之链表
白帽子九一
04-22 955
BM1 反转链表 描述 给定一个单链表的头结点pHead(该头节点是有值的，比如在下图，它的val是1)，长度为n，反转该链表后，返回新链表的表头。 数据范围： 0\leq n\leq10000≤n≤1000 要求：空间复杂度 O(1)O(1) ，时间复杂度 O(n)O(n) 。 如当输入链表{1,2,3}时， 经反转后，原链表变为{3,2,1}，所以对应的输出为{3,2,1}。 以上转换过程如下图所示： 题解思路 将链表反转，就是将每个表元的指针从向后变成向前，那我们可以遍历原始链表，将遇到的节点一一指
【牛客面试必刷101】-合并两个有序的数组+二分查找+两数之和
孙宇航的博客
12-07 215
对于Java lang包中 arraycopy方法解释： 两数之和
leetcode/牛客 链表面试题
TPON的博客
05-26 344
leetcode/牛客 链表面试题
【牛客面试必刷TOP101】Day24.BM34 判断是不是二叉搜索树和BM35 判断是不是完全二叉树
未央的博客哟
02-21 513
一、BM16 删除有序链表中重复的元素-II题目描述给定一个二叉树根节点，请你判断这棵树是不是二叉搜索树。二叉搜索树满足每个节点的左子树上的所有节点均小于当前节点且右子树上的所有节点均大于当前节点。举例说明：示例1：题目解析二、BM35 判断是不是完全二叉树题目描述给定一个二叉树，确定他是否是一个完全二叉树。完全二叉树的定义：若二叉树的深度为 h，除第 h 层外，其它各层的结点数都达到最大个数，第 h 层所有的叶子结点都连续集中在最左边，这就是完全二叉树。
Leetcode面试热题（二）
weixin_38428439的博客
09-30 273
下面是题 1、采用两个栈组成一个队列 class MyQueue { private: stack<int> inStack, outStack; void in2out() { while (!inStack.empty()) { outStack.push(inStack.top()); inStack.pop(); } } public: MyQueue() {}..
C++面试整理
csdn609387481的博客
11-07 7928
最近开始准备找实习了，收到某位大佬的指导，说可以上牛客网把相关的面经都刷一遍，记录下考点各个击破。大佬是搞java的，已经把java的刷完了，看了一下觉得很受用，因此也准备刷下c++的。顺带附上大佬的java总结：https://zhuanlan.zhihu.com/p/266362976 ...
牛客面试算法top101（JAVA和C++）
04-30
牛客面试算法top101（JAVA和C++）
【牛客面试必刷101】二叉树的前序遍历+二叉树的中序遍历+二叉树的后序遍历
孙宇航的博客
12-06 240
二叉树的中序遍历 二叉树的后序遍历
top面试101.对称二叉树
carolineme的博客
08-02 113
题目描述： 思路一：递归 /** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode(int x) : val(x), left(NULL), right(NULL) {} * }; */ class Solution { public: bool check(Tree
牛客网刷题总结--面试必刷top101
老板来片烤面包的博客
06-02 469
解法2：
牛客-NC70-单链表的排序
dingzhi4469的博客
07-22 392
NC70. 单链表的排序（easy）方法一：归并排序（递归） 方法一：归并排序（递归） 思路：这道题考察链表排序问题，朴素解法（暴力解）是直接遍历存值再遍历修改值；但更容易打动面试官的可能是归并排序了吧。 我们分两步完成该题，首先是分割，怎么分？需要使用快慢指针去寻找链表的中点，然后以中点为分割点，将链表分为左链表和右链表。再递归进行分割，当head == null || head.next == null达到递归终止条件。如下图的递归终止图，ps：图片来自于K神。 举个例子：left = 3， righ
054、牛客网算法面试必刷TOP101--堆/栈/队列（230509）
Yora123的博客
05-09 1162
本文章记录自己刷牛客网算法面试必刷TOP101——堆/栈/队列面试必刷TOP101——堆/栈/队列，总共有8道题目。提示：以下是本篇文章正文内容。
LeetCode，牛客面试必刷，看了这些，大厂面试必问
m0_64604842的博客
12-04 767
一、BAT等大厂面试问题套路总结 我们先来看看各个大厂面试答题流程 阿里巴巴 腾讯 百度 小米 看上面的面试题，都是牛客网里随便搜的，我用红色圈出来的，都是大厂面试时，最喜欢问的Android知识点，几乎每家大厂必问！ 面试，开始： 1.自我介绍 2.计算机网络基础面试题 3.数据结构与算法题 4.java面试题 5.Android面试题 6.如果有幸前面都过了开始HR面试，我就称为非技术题 7.其他一些扩展题，这是面试官按照你的能力提出的一些问题，（这些会是加分项哦！）以及你简历上写的项目与.
牛客必刷TOP101——模拟
最新发布
weixin_42486554的博客
02-17 873
一个数组A中存有 n 个整数，在不允许使用另外数组的前提下，将每个整数循环向右移 M（ M >=0）个位置，即将A中的数据由（A0 A1 ……可以把例题矩阵画出来，对比原矩阵和旋转90度后的矩阵，可以得知，只需要将原矩阵先按照左斜对角线翻转，然后每一行再进行翻转，即可得到旋转90度后的矩阵。将矩阵旋转90度，即原来的最后一行变成新矩阵的第一列，依此类推，所以可以先定义一个新矩阵，然后按照关系依此对新矩阵进行赋值即可。给定一个m x n大小的矩阵（m行，n列），按螺旋的顺序返回矩阵中的所有元素。
牛客TOP101学习笔记
且视他人之疑目如盏盏鬼火,大胆走吾之夜路！
04-01 1463
这里写目录标题一 链表BM1反转链表BM2链表内指定区间反转BM3链表中的节点每k个一组翻转BM4 合并两个排序的链表BM5 合并k个已排序的链表BM6 判断链表中是否有环BM7 链表中环的入口结点BM8 链表中倒数最后k个结点BM9 删除链表的倒数第n个节点BM10 两个链表的第一个公共结点BM11 链表相加(二)BM12 单链表的排序**BM13 判断一个链表是否为回文结构BM14 链表的奇偶重排BM15 删除有序链表中的重复元素-ⅠBM16 删除链表中的重复元素-Ⅱ二 数组**BM17** 二分查找.
牛客面试算法TOP101：JAVA与C++解析
"牛客面试算法top101（JAVA和C++）提供了101个热门的算法题目，包括PDF和HTML格式，旨在帮助求职者准备面试。在NowCoder平台上可以找到相关的在线编程题目集，涵盖了算法分类，适合进行算法刷题。此资源可能包含从...
评论 2
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值