0x03.1_前缀和

前缀和是指某序列的前n项和，可以把它理解为数学上的数列的前n项和，而差分可以看成前缀和的逆运算。合理的使用前缀和与差分，可以将某些复杂的问题简单化。

(1).

对于一维前缀和，可以很好的解决 ——“一个长度为n的整数序列。有m个询问，每个询问输入一对l, r。对于每个询问，输出原序列中从第l个数到第r个数的和。”这个问题，使得时间复杂度降为 O(1);

原理

sum[r] =a[1]+a[2]+a[3]+a[l-1]+a[l]+a[l+1]......a[r];
sum[l-1]=a[1]+a[2]+a[3]+a[l-1];
sum[r]-sum[l-1]=a[l]+a[l+1]+......+a[r];

图解

(2). 

 对于二维前缀和：可以很好的解决—— “一个n行m列的整数矩阵，有 q 个询问，每个询问包含四个整数x1, y1, x2, y2，表示一个子矩阵的左上角坐标和右下角坐标。对于每个询问输出子矩阵中所有数的和。”这个问题。

同一维前缀和一样，我们先来定义一个二维数组s[][], s[i][j]表示二维数组中，左上角(1,1)到右下角( i,j )所包围的矩阵元素的和。接下来推导二维前缀和的公式。

先看一下一张图：

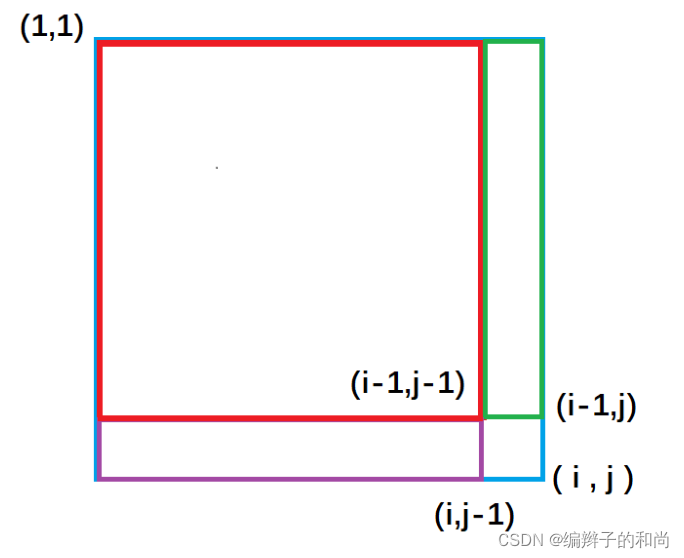
紫色面积是指(1,1)左上角到(i,j-1)右下角的矩形面积, 绿色面积是指(1,1)左上角到(i-1, j )右下角的矩形面积。每一个颜色的矩形面积都代表了它所包围元素的和。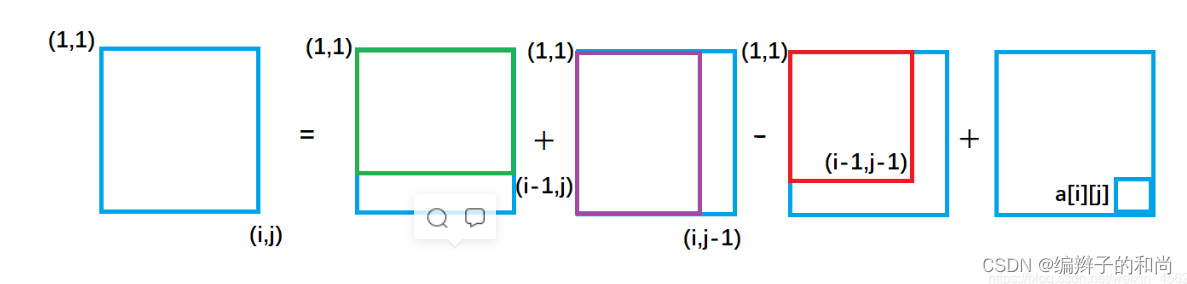

从图中我们很容易看出，整个外围蓝色矩形面积s[i][j] = 绿色面积s[i-1][j] + 紫色面积s[i][j-1] - 重复加的红色的面积s[i-1][j-1]+小方块的面积a[i][j];

因此得出二维前缀和预处理公式

s[i] [j] = s[i-1][j] + s[i][j-1 ] + a[i] [j] - s[i-1][ j-1]

接下来回归问题去求以(x1,y1)为左上角和以(x2,y2)为右下角的矩阵的元素的和。

如图：
 

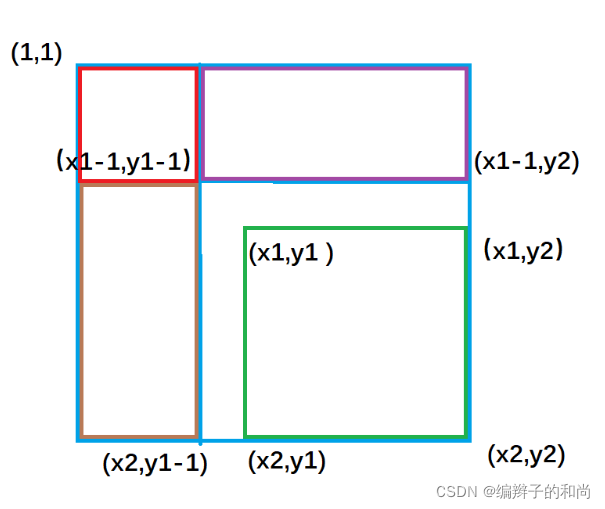
紫色面积是指 ( 1,1 )左上角到(x1-1,y2)右下角的矩形面积 ，黄色面积是指(1,1)左上角到(x2,y1-1)右下角的矩形面积；

不难推出：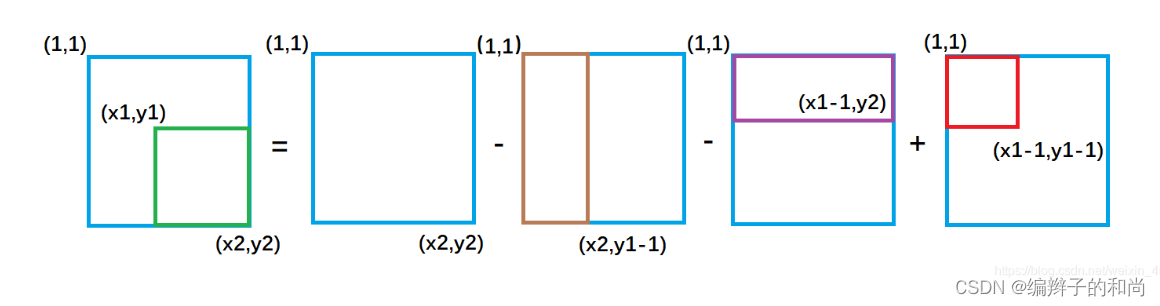

绿色矩形的面积 = 整个外围面积s[x2, y2] - 黄色面积s[x2, y1 - 1] - 紫色面积s[x1 - 1, y2] + 重复减去的红色面积 s[x1 - 1, y1 - 1]

因此二维前缀和的结论为：

以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵的和为：
s[x2, y2] - s[x1 - 1, y2] - s[x2, y1 - 1] + s[x1 - 1, y1 - 1]
 

接下来练习一道题目：

问题描述：

地图上有 N 个目标，用整数 Xi,Yi 表示目标在地图上的位置，每个目标都有一个价值 Wi。

注意：不同目标可能在同一位置。

现在有一种新型的激光炸弹，可以摧毁一个包含 R×R 个位置的正方形内的所有目标。

激光炸弹的投放是通过卫星定位的，但其有一个缺点，就是其爆炸范围，即那个正方形的边必须和 x，y 轴平行。

求一颗炸弹最多能炸掉地图上总价值为多少的目标。

输入格式

第一行输入正整数 N 和 R，分别代表地图上的目标数目和正方形的边长，数据用空格隔开。

接下来 N 行，每行输入一组数据，每组数据包括三个整数 Xi,Yi,Wi，分别代表目标的 x 坐标，y 坐标和价值，数据用空格隔开。

输出格式

输出一个正整数，代表一颗炸弹最多能炸掉地图上目标的总价值数目。

数据范围

0≤R≤109
0<N≤10000,
0≤Xi,Yi≤5000
0≤Wi≤1000

输入样例：

2 1
0 0 1
1 1 1

输出样例：

1

AC代码：

#include <iostream>
using namespace std;

const int N = 5010;

int f[N][N];

int main()
{
	int N, R;
	cin >> N >> R;
	int n = R, m = R;
	for(int i = 0, x, y, w; i < N; i ++ )
	{
		cin >> x >> y >> w;
		x ++, y ++;
		n = max(n, x), m = max(m, y);
		f[x][y] += w;
	}
	
	for(int i = 1; i <= n; i ++ )
	{
		for(int j = 1; j <= m; j ++ )
		{
			f[i][j] += f[i - 1][j] + f[i][j - 1] - f[i - 1][j - 1];
		}
	}
	
	int res = 0;
	for(int i = R; i <= n; i ++ )
	{
		for(int j = R; j <= m; j ++ )
		{
			res = max(res, f[i][j] - f[i - R][j] - f[i][j - R] + f[i - R][j - R]);
		}
	}
	
	cout << res << endl;
	return 0;
}

 

 具体请见：

https://blog.youkuaiyun.com/weixin_45629285/article/details/111146240