本文介绍了Huffman树的概念，如何通过构造算法生成最优二叉树，并详细阐述了哈夫曼编码在数据压缩中的应用。通过实例演示了如何使用Huffman编码对字符进行可变长度编码，以及其实现步骤和压缩效果。
目录
一、Huffman树（最优二叉树）
1、定义
树的带权路径长度，就是树中所有的叶节点的权值乘上其到根节点的路径长度。
在含有n 个带权叶结点的二叉树中，其中带权路径长度（WPL）最小的二叉树称为哈夫曼树， 也称最优二叉树。如图，c树的WPL=35最小，经验证其为哈夫曼树。
2、构造
构造哈夫曼树的算法
（给定n 个权值分别为wi的结点）
1）将这n个结点分别作为n棵仅含一个结点的二叉树，构成森林F。
2）构造一个新结点，从 F 中选取两棵根结点权值最小的树作为新结点的左、右子树，并且将新结点的权值置为左、右子树上根结点的权值之和。
3）从 F 中删除刚才选出的两棵树，同时将新得到的树加入F中。
4）重复步骤2）和 3）, 直至F中只剩下一棵树为止。
//哈夫曼
class Node implements Comparable<Node> {
Byte data;
int weight;
Node left;
Node right;
public Node(Byte data, int weight) {
this.data = data;
this.weight = weight;
}
@Override
public int compareTo(Node o) {
return this.weight - o.weight;
}
@Override
public String toString() {
return "Node [ data = " + data + "weight = " + weight + " ]";
}
//遍历
public void preOrder() {
System.out.println(this);
if (this.left != null) {
this.left.preOrder();
}
if (this.right != null) {
this.right.preOrder();
}
}
}
private static Node createHuffmanTree(List<Node> nodes) {
/**
*@MethodName createHuffmanTree
*@Description TODO 创建哈夫曼树
*@Author SSRS
*@Date 2020-10-31 13:21
*@Param [nodes]
*@ReturnType Java_note.Algorithm.HuffmanCode.Node
*/
while (nodes.size() > 1) {
//排序
Collections.sort(nodes);
//取最小两个二叉树
Node leftNode = nodes.get(0);
Node rightNode = nodes.get(1);
//创建新的二叉树（他的根节点没有data，只有权值）
Node parent = new Node(null, leftNode.weight + rightNode.weight);
parent.left = leftNode;
parent.right = rightNode;
//删除已用结点
nodes.remove(leftNode);
nodes.remove(rightNode);
//加入新节点
nodes.add(parent);
}
return nodes.get(0);
}哈夫曼树特点
1）每个初始结点最终都成为叶结点，且权值越小的结点到根结点的路径长度越大。
2）构造过程中共新建了n-1个结点 （双分支结点），因此哈夫曼树的结点总数为2n- 1 。
3）每次构造都选择 2 棵树作为新结点的孩子，因此哈夫曼树中不存在度为1 的结点。
例如，权值｛7, 5, 2, 4｝的哈夫曼树的构造过程如图所示。
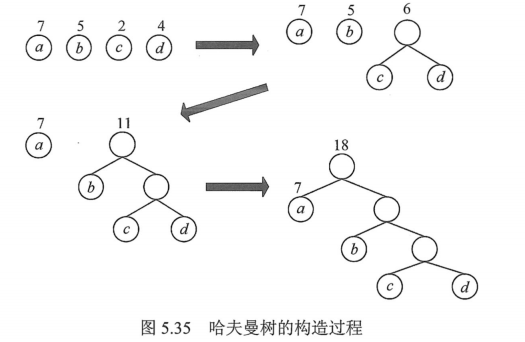
二、Huffman编码
在数据通信中，若对每个字符用相等长度的二进制位表示，称这种编码方式为固定长度编码。 若允许对不同字符用不等长的二进制位表示，则这种编码方式称为可变长度编码。
可变长度编码 比固定长度编码要好得多，其特点是对频率高的字符赋以短编码，而对频率较低的字符则赋以较长一些的编码，从而可以使字符的平均编码长度减短，起到压缩数据的效果。哈夫曼编码是一种被广泛应用而且非常有效的数据压缩编码。
若没有一个编码是另一个编码的前缀，则称这样的编码为前缀编码。哈夫曼编码是前缀编码。
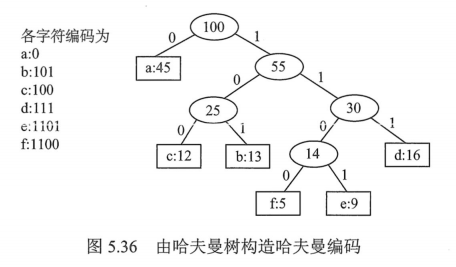
class HuffmanCode {
public static void main(String[] args) {
String str = "I like like like java Do you like a java";
byte[] strBytes = str.getBytes();
System.out.println(str + "的原长度是" + strBytes.length);
HuffmanCode huffmanCode = new HuffmanCode();
System.out.println("转成哈夫曼编码为：");
String huffmanstr = huffmanCode.createHuffmanCode(strBytes);
System.out.println(huffmanstr);
System.out.println("其长度为：" + huffmanstr.getBytes().length);
byte[] bytes = huffmanCode.zipbytes(strBytes);
System.out.println("压缩后的结果是：" + Arrays.toString(bytes));
System.out.println("其长度为：" + bytes.length);
System.out.println("解压缩：" + new String(huffmanCode.rezip(bytes)));
}
private static List<Node> getNodes(byte[] bytes) {
/**
*@MethodName getNodes
*@Description TODO 获得构建哈夫曼树的Node
*@Author SSRS
*@Date 2020-10-31 13:07
*@Param [bytes]
*@ReturnType java.util.List<Java_note.Algorithm.HuffmanCode.Node>
*/
ArrayList<Node> nodes = new ArrayList<Node>();//要返回的nodes集合
Map<Byte, Integer> counts = new HashMap<>();
//统计每一个byte出现的次数
for (byte b : bytes) {
Integer count = counts.get(b);
if (count == null) {
counts.put(b, 1);
} else {
counts.put(b, count + 1);
}
}
//把每一个键值对转换成Node对象，并加入nodes集合
for (Map.Entry<Byte, Integer> each : counts.entrySet()) {
nodes.add(new Node(each.getKey(), each.getValue()));
}
return nodes;
}
private static Node createHuffmanTree(List<Node> nodes) {
/**
*@MethodName createHuffmanTree
*@Description TODO 创建哈夫曼树
*@Author SSRS
*@Date 2020-10-31 13:21
*@Param [nodes]
*@ReturnType Java_note.Algorithm.HuffmanCode.Node
*/
while (nodes.size() > 1) {
//排序
Collections.sort(nodes);
//取最小两个二叉树
Node leftNode = nodes.get(0);
Node rightNode = nodes.get(1);
//创建新的二叉树（他的根节点没有data，只有权值）
Node parent = new Node(null, leftNode.weight + rightNode.weight);
parent.left = leftNode;
parent.right = rightNode;
//删除已用结点
nodes.remove(leftNode);
nodes.remove(rightNode);
//加入新节点
nodes.add(parent);
}
return nodes.get(0);
}
static Map<Byte, String> codes = new HashMap<Byte, String>();
private static Map<Byte, String> getCodes(Map<Byte, String> codes, Node node, String code, StringBuilder stringBuilder) {
StringBuilder stringBuilder1 = new StringBuilder(stringBuilder);
stringBuilder1.append(code);
if (node != null) {
if (node.data == null) {
getCodes(codes, node.left, "0", stringBuilder1);
getCodes(codes, node.right, "1", stringBuilder1);
} else {
codes.put(node.data, stringBuilder1.toString());
}
}
return codes;
}
private static byte[] bytesArrays(String string) {
int len;//bytes数组长度
if (string.length() % 8 == 0) {
len = string.length() / 8;
} else {
len = string.length() / 8 + 1;
}
int index = 0;//bytes角标
byte[] huffmanCodeBytes = new byte[len];
for (int i = 0; i < string.length(); i += 8) {
String strTemp;
if (i + 8 > string.length()) {
strTemp = string.substring(i);
} else {
strTemp = string.substring(i, i + 8);
}
//转换
huffmanCodeBytes[index] = (byte) Integer.parseInt(strTemp, 2);
index++;
}
return huffmanCodeBytes;
}
public static String createHuffmanCode(byte[] bytes) {
/**
*@MethodName createHuffmanCode
*@Description TODO 得到哈夫曼转码
*@Author SSRS
*@Date 2020-10-31 20:15
*@Param [bytes]
*@ReturnType java.lang.String
*/
Node root = createHuffmanTree(getNodes(bytes));
StringBuilder stringBuilder = new StringBuilder();
getCodes(codes, root, "", stringBuilder);
String str = "";
for (Byte each : bytes) {
str += codes.get(each);
}
return str;
}
public byte[] zipbytes(byte[] bytes) {
return bytesArrays(createHuffmanCode(bytes));
}
//解压缩
private String byteToBitString(boolean flag, byte b) {
/**
*@MethodName byteToBitString
*@Description TODO 将一个byte转成二进制字符串
*@Author SSRS
*@Date 2020-10-31 20:56
*@Param [flag 正数为true要补高位, b]
*@ReturnType java.lang.String
*/
int temp = b;//转int
//如果是正数还要补高位
if (flag) {
temp |= 256;//按位与 256 是 1 0000 0000 | 0000 0001=》1 0000 0001
}
String str = Integer.toBinaryString(temp);//返回的是二进制的补码
if (flag) {
return str.substring(str.length() - 8);
} else {
return str;
}
}
public byte[] rezip(byte[] huffmanbytes) {
StringBuilder stringBuilder = new StringBuilder();//储存二进制字符串
//全部转成二进制字符串
for (int i = 0; i < huffmanbytes.length; i++) {
//如果是最后一个可能不满8位就转码的那个就不用补高位无论正负，因此要判断
boolean flag = (i == huffmanbytes.length - 1);
stringBuilder.append(byteToBitString(!flag, huffmanbytes[i]));
}
//把哈夫曼编码表反向
Map<String, Byte> map = new HashMap<String, Byte>();
for (Map.Entry<Byte, String> each : codes.entrySet()) {
map.put(each.getValue(), each.getKey());
}
List<Byte> list = new ArrayList();//解压缩后的语句的储存位置
for (int i = 0; i < stringBuilder.length(); ) {
int count = 1;//计数,计每一个字符的二进制字符位数
boolean flag = true;
Byte b = null;
//找字符对应哈夫曼编码
while (flag) {
String key = stringBuilder.substring(i, i + count);
b = map.get(key);
if (b == null) {
count++;
} else {//匹配成功
flag = false;
}
}
list.add(b);
i = i + count;
}
byte b[] = new byte[list.size()];
for (int i = 0; i < b.length; i++) {
b[i] = list.get(i);
}
return b;
}
public void preOrder(Node root) {
if (root != null) {
root.preOrder();
} else {
System.out.println("二叉树为空。");
}
}
}
本文所有概念性描述及图示均来自王道考研数据结构一书
扫一扫
280
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
