概念
四连通区域:指从某个点出发,只能通过上、下、左、右四个方向的运动到达区域内的其他点,且不能跨越区域的边界。
八连通区域:除了上、下、左、右四个方向,还可以沿对角线方向(左上、右上、左下、右下)运动,同样不能跨越区域的边界。
示例解释
下面通过一些简单的图形示例来解释四连通和八连通区域个数的判断:
示例一:简单的矩形区域
假设我们有一个简单的矩形区域,如下所示:

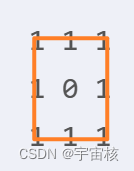
这里的数字1代表该位置属于某个区域,而0代表不属于该区域。
- 四连通区域个数:在这个例子中,我们可以看到1组成的区域是四连通的,因为它们只能通过上、下、左、右四个方向相连。因此,四连通区域个数为1。
- 八连通区域个数:由于这个区域没有对角线方向的连接,但是按照八连通的定义,这些区域仍然是独立的。因此,八连通区域个数也为1。
示例二:包含对角线连接的区域
现在考虑一个包含对角线连接的区域:


- 四连通区域个数:这个区域虽然视觉上是一个整体,但按照四连通的定义,它仍然是由多个小的四连通区域组成(如果考虑每个单独的1为一个区域)。因此,如果我们这样看待,四连通区域个数仍然是多个。但如果我们将整个连续的1看作一个区域,那么四连通区域个数就是1。
- 八连通区域个数:按照八连通的定义,这个区域是一个整体的八连通区域,因为任意一点都可以通过八个方向之一到达区域内的其他点。所以八连通区域个数为1。
示例三:不规则区域1



- 四连通区域个数:如果我们将整个连续的1看作一个区域,那么四连通区域个数就是2。
- 八连通区域个数:这个区域是一个整体的八连通区域,因为任意一点都可以通过八个方向之一到达区域内的其他点。所以八连通区域个数为1。
示例四:不规则区域2



- 四连通区域个数:如果我们将整个连续的1看作一个区域,那么四连通区域个数就是2。
- 八连通区域个数:这个区域是一个整体的八连通区域,因为任意一点都可以通过八个方向之一到达区域内的其他点。所以八连通区域个数为1。























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








