NMS 多个框中取最大值

在MNS计算中，取预测框与真实框的交集，需要算出[xmin,ymin,xmax,ymax]，那对于多对多的情况下，如何实现批量计算呢？如下代码所示：

def compute_intersection(set_1, set_2):
    """
    计算anchor之间的交集
    Args:
        set_1: a tensor of dimensions (n1, 4), anchor表示成(xmin, ymin, xmax, ymax)
        set_2: a tensor of dimensions (n2, 4), anchor表示成(xmin, ymin, xmax, ymax)
    Returns:
        intersection of each of the boxes in set 1 with respect to each of the boxes in set 2, shape: (n1, n2)
    """
    # PyTorch auto-broadcasts singleton dimensions
    lower_bounds = torch.max(set_1[:, :2].unsqueeze(1), set_2[:, :2].unsqueeze(0))  # (n1, n2, 2)
    upper_bounds = torch.min(set_1[:, 2:].unsqueeze(1), set_2[:, 2:].unsqueeze(0))  # (n1, n2, 2)
    intersection_dims = torch.clamp(upper_bounds - lower_bounds, min=0)  # (n1, n2, 2)
    return intersection_dims[:, :, 0] * intersection_dims[:, :, 1]  # (n1, n2)

这时候，torch.max 的boradcast就可以派上用场了。
set_1 的shape,从 (n1, 4) 进行unsqueeze(1)，从而得到 （n1,1, 2）
set_1 的shape,从 (n2, 4) 进行unsqueeze(0)，从而得到 （1,n2, 2）
这是使用torch.max（）函数，最后得到shape为 [n1,n2,2],如下图所示：

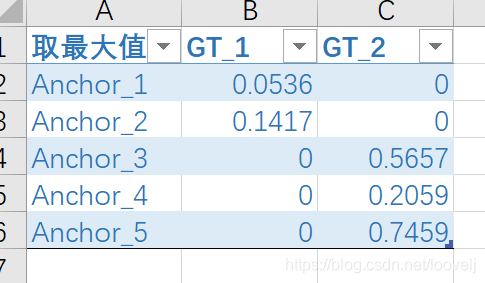
然后再继续计算NMS

def compute_jaccard(set_1, set_2):
    """
    计算anchor之间的Jaccard系数(IoU)
    Args:
        set_1: a tensor of dimensions (n1, 4), anchor表示成(xmin, ymin, xmax, ymax)
        set_2: a tensor of dimensions (n2, 4), anchor表示成(xmin, ymin, xmax, ymax)
    Returns:
        Jaccard Overlap of each of the boxes in set 1 with respect to each of the boxes in set 2, shape: (n1, n2)
    """
    # Find intersections
    intersection = compute_intersection(set_1, set_2)  # (n1, n2)

    # Find areas of each box in both sets
    areas_set_1 = (set_1[:, 2] - set_1[:, 0]) * (set_1[:, 3] - set_1[:, 1])  # (n1)
    areas_set_2 = (set_2[:, 2] - set_2[:, 0]) * (set_2[:, 3] - set_2[:, 1])  # (n2)

    # Find the union
    # PyTorch auto-broadcasts singleton dimensions
    union = areas_set_1.unsqueeze(1) + areas_set_2.unsqueeze(0) - intersection  # (n1, n2)   #这个地方也用到了交叉计算，通过错位，就能通过广播算到所有可能的结果

    return intersection / union  # (n1, n2)