八皇后问题--如何计算皇后的攻击范围

计算一个皇后的攻击范围，本质上就是找出棋盘上所有会被她直接攻击到的位置。国际象棋中的皇后可以横向、纵向、斜向无限移动，因此她的攻击范围可以用以下规则判断：

---

1. 皇后攻击范围的直观理解

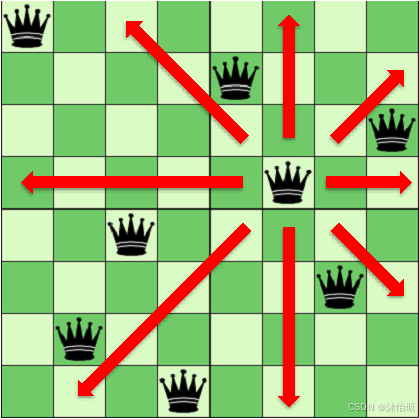
假设皇后在位置 (row, col)（行和列从0或1开始编号均可），她的攻击范围覆盖：

• 整行：同一行的所有列。
• 整列：同一列的所有行。
• 两条斜线：左上到右下（主对角线）和右上到左下（副对角线）的所有位置。
  

---

2. 数学判断条件

要判断任意位置 (i, j) 是否在皇后 (row, col) 的攻击范围内，只需满足以下任意一个条件：

1. 在同一行：i == row
2. 在同一列：j == col
3. 在同一主对角线：i - row == j - col（行差 = 列差）
4. 在同一副对角线：i - row == -(j - col)（行差 = -列差）
   （或简化为 i + j == row + col）

---

3. 例子说明

假设皇后在 (4,4)（第5行第5列，假设从0开始编号）：

• 横向攻击范围：所有 (4, j)，比如 (4,0)、(4,7)。
• 纵向攻击范围：所有 (i, 4)，比如 (0,4)、(7,4)。
• 主对角线：行差=列差，如 (1,1)、(5,5)、(7,7)。
• 副对角线：行差= -列差，如 (1,7)、(5,3)、(7,1)。

---

4. 代码实现思路

在编程中（比如解决八皇后问题时），通常用以下逻辑判断两个皇后是否冲突：

def is_attackable(q1_row, q1_col, q2_row, q2_col):
    # 同一行或同一列
    if q1_row == q2_row or q1_col == q2_col:
        return True
    # 主对角线或副对角线
    if abs(q1_row - q2_row) == abs(q1_col - q2_col):
        return True
    return False

---

5. 为什么不用遍历整个棋盘？

在实际问题（如八皇后）中，我们通常不需要显式计算所有攻击位置，而是用上述规则直接判断新皇后与已有皇后的位置关系。这样效率更高！

---

6. 边界问题

• 棋盘边界（如0行或7行）不影响规则，因为判断条件与具体行列值无关。
• 如果棋盘不是8x8（比如N皇后问题），规则依然适用。

---

总结

• 皇后的攻击范围 = 同行 + 同列 + 两条斜线。
• 数学本质是行差和列差的绝对值相等，或行列直接相等。
• 实际编程中只需判断新皇后与已有皇后的位置关系，无需遍历整个棋盘。