k-means获取最佳k值：手肘法与轮廓系数法

最新推荐文章于 2025-05-09 00:00:30 发布
最新推荐文章于 2025-05-09 00:00:30 发布
阅读量1.8k 收藏 3
点赞数
CC 4.0 BY-SA版权
分类专栏： 机器学习 数据分析 文章标签： kmeans 聚类 机器学习
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/lm_is_dc/article/details/130536652
本文介绍了确定k-means聚类中最佳k值的两种方法：手肘法和轮廓系数法。通过计算误差平方和（SSE）和轮廓系数，分析得出在给定数据集上，k=11时达到最优聚类效果。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

1、手肘法

获取最佳的k值
1、手肘法的核心指标是SSE(sum of the squared errors，误差平方和)，
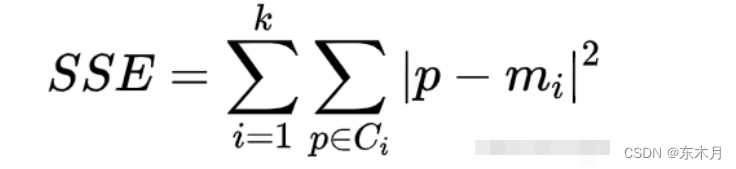
在这里插入图片描述

其中，Ci是第i个簇，p是Ci中的样本点，mi是Ci的质心（Ci中所有样本的均值），SSE是所有样本的聚类误差，代表了聚类效果的好坏。
手肘法的核心思想是：随着聚类数k的增大，样本划分会更加精细，每个簇的聚合程度会逐渐提高，
那么误差平方和SSE自然会逐渐变小。并且，当k小于真实聚类数时，由于k的增大会大幅增加每个簇的聚合程度，
故SSE的下降幅度会很大，而当k到达真实聚类数时，再增加k所得到的聚合程度回报会迅速变小，
所以SSE的下降幅度会骤减，然后随着k值的继续增大而趋于平缓，也就是说SSE和k的关系图是一个手肘的形状，
 而这个肘部对应的k值就是数据的真实聚类数。
 当然，这也是该方法被称为手肘法的原因。

代码：

from sklearn.cluster import KMeans
from matplotlib
了解本专栏 订阅专栏 解锁全文 超级会员免费看
关于利用K-均值法测定
06-04
在本文中，我们考虑结合确定性退火方法和Tsallis熵最大化的模糊c均值（FCM）聚类算法。 Tsallis熵是Shannon熵的q参数扩展。 通过在FCM框架内最大化Tsallis熵，可以推导出类似于统计机械分布函数的隶属函数。 使用此方法时的主要考虑因素之一是如何为给定的数据集确定合适的q值和最高退火温度Thigh。 因此，在本文中，提出了一种在不引入任何附加参数的情况下同时确定这些值的方法。 在我们的方法中，隶属函数通过一系列扩展方法进行近似，并且K-means聚类算法被用作预处理步骤以估计每个数据分布的半径。 实验结果表明，该方法是有效的，并且可以根据给定的数据集自动和代数确定q和Thigh。
确定最佳聚类数matlab代码_K-means聚类最优k值的选取
weixin_39606019的博客
11-26 6451
最近做了一个数据挖掘的项目，挖掘过程中用到了K-means聚类方法，但是由于根据行业经验确定的聚类数过多并且并不一定是我们获取到数据的真实聚类数，所以，我们希望能从数据自身出发去确定真实的聚类数，也就是对数据而言的最佳聚类数。为此，我查阅了大量资料和博客资源，总结出主流的确定聚类数k的方法有以下两类。1.手肘法1.1 理论手肘法的核心指标是SSE(sum of the squared errors...
Python: K-Means聚类，肘部法则+轮廓系数确定最佳K值
最新发布
Qiaomwh的博客
05-09 480
轮廓系数（Silhouette Coefficient）是一种用于评估聚类效果的指标，它结合了簇内凝聚度和簇间分离度来衡量每个样本点与所属簇的匹配程度，以及与其他簇的分离程度。轮廓系数的取值范围是 [−1,1]，值越接近 1 表示聚类效果越好，值接近 -1 表示样本点可能被错误地分配到了其他簇，值接近 0 表示样本点位于两个簇的边界上。这个点通常被认为是最佳的 K 值，因为在该点之前，增加 K 值能显著降低惯性，而在该点之后，增加 K 值对惯性的改善效果不明显，同时还会增加模型的复杂度和计算成本。
KNN算法 通过手肘法选取最优参数K(鸢尾花的数据)
吃饭的博客
12-20 1万+
实验目的：熟悉手肘法和KNN聚类 实验内容：针对iris数据集（相关信息详见https://archive.ics.uci.edu/ml/datasets/iris），进行KNN 分类模型的python实现，通过手肘法选取最优参数K（K不用超过10），并给出最优参数下以下新数据点的预测类别，并进行可视化（突出新数据点的位置，可视化所有数据的类别）： （1）4.5，3.4， 2.1， 0.8 （2）5.5，2.4， 7.3， 1.5 （3）7.6， 3.3， 5.7， 5.2 通过手肘法选取最优参数K（K
KMeans算法，采用肘部法则获取类簇中心个数K的值。
weixin_46613998的博客
10-13 6672
K-Means是一种非常常见的聚类算法，在处理聚类任务中经常使用，K-Means算法是一种原型聚类算法。 该算法重要的一步就是确定K的值的划分，通常我们采用肘部法则选取K值，再依据轮廓系数，及各个数据集中数据的数量综合去评估哪个K值为最佳。 肘部法则 1 ）、对于n个点的数据集，迭代计算k from 1 to n，每次聚类完成后计算每个点到其所属的簇中心的距离的平方和； 2）、平方和是会逐渐变小的，直到k时平方和为0，因为每个点都是它所在的簇中心本身。 3）、在这个平方和变化过程中..
K-means聚类最优k值的选取
热门推荐
qq_15738501的博客
01-11 8万+
       最近做了一个数据挖掘的项目，挖掘过程中用到了K-means聚类方法，但是由于根据行业经验确定的聚类数过多并且并不一定是我们获取到数据的真实聚类数，所以，我们希望能从数据自身出发去确定真实的聚类数，也就是对数据而言的最佳聚类数。为此，我查阅了大量资料和博客资源，总结出主流的确定聚类数k的方法有以下两类。1.手肘法1.1 理论手肘法的核心指标是SSE(sum of the squared...
数学建模：K-means聚类手肘法确定k值（含python实现）
zly_Always_be的博客
02-13 1万+
数学建模：K-means聚类手肘法确定k值（含python实现）
K-means算法的实践与应用：最佳聚类数确定与散点图可视化结果展示,K-means算法及其在确定最佳聚类数与散点图分析中的应用：通过手肘法、轮廓系数法及CH值综合衡量及聚类结果可视化的Python实
03-04
K-means算法的实践与应用：最佳聚类数确定与散点图可视化结果展示,K-means算法及其在确定最佳聚类数与散点图分析中的应用：通过手肘法、轮廓系数法及CH值综合衡量及聚类结果可视化的Python实践。,Kmeans算法、最佳...
数据挖掘中手肘法用于k-means聚类算法选k值的技术解析与Python实现
03-29
内容概要：本文详细介绍了手肘法在k-means聚类算法中选择最佳k值的方法及其Python实现。首先通过模拟数据展示了如何生成数据并使用k-means进行初步聚类。接着深入探讨了手肘法的核心思想，即通过绘制SSE（误差平方和...
基于手肘法的k-means聚类
05-05
接着，利用sklearn库实现了k-means算法，计算不同k值对应的SSE（簇内平方和），并通过绘制手肘图找出最佳k值。文中还讨论了手肘法的局限性和应对措施，如结合轮廓系数和其他评估指标，以及针对不同类型数据的特点...
数据挖掘中基于手肘法的k-means聚类算法及其Python实现与优化
04-15
接着，利用sklearn库实现了k-means算法，计算不同k值对应的SSE（簇内平方和），并通过绘制手肘图找出最佳k值。文中还讨论了手肘法的局限性和应对措施，如结合轮廓系数和其他评估指标，以及针对不同类型数据的特点...
KMeans_elbow：使用“肘标准”为K-means算法确定最佳聚类数的代码
02-03
KMeans算法和Elbow准则 “ k-Means聚类背后的想法是获取一堆数据并确定数据中是否存在任何自然聚类（相关对象的组）。 k-Means算法是所谓的无监督学习算法。 我们事先不知道数据中存在什么模式-它没有形式分类-但我们想知道是否可以将数据以某种方式分为几类。 例如，您可以使用k-Means通过告诉像素根据其颜色值将像素分组为3个群集来查找图像中3种最突出的颜色。 或者，您可以使用它将相关新闻文章分组在一起，而无需事先确定要使用的类别。 该算法将自动找出最佳组。 k均值中的“ k”是一个数字。 该算法假定数据中存在k个中心，各个数据元素分散在周围。 最接近这些所谓质心的数据将被分类或分组在一起。 k-Means不会告诉您每个特定数据组的分类器是什么。 将新闻文章分成几组后，并不能说第一组是关于科学的，第二组是关于名人的，第三组是关于即将举行的选举的，等等。您只知道相关的新闻故事现在在一起了，但不一定是什么这种关系意味着。 k均值仅有助于寻找潜在的集群。” -取自对算法的移植。 存储库包含： 将的模型拟合到。 使用“肘标准”为K-means算法确定最佳聚类数的
Kmeans聚类算法-手肘法
01-08
Kmeans聚类算法-手肘法，jupyter notebook 编写，打开可以直接运行，使用iris等5个数据集，机器学习。
肘部法和轮廓系数法确定K-means中的k值
weixin_46713695的博客
06-10 1万+
K-Means算法如何确定k值
使用肘部法则选择KMeans聚类中的k值
python收藏家的博客
12-05 1万+
任何无监督算法的基本步骤是确定数据可以被聚类到的聚类的最佳数量。因为我们在无监督学习中没有任何预定义数量的聚类。我们倾向于使用一些可以帮助我们决定最佳聚类数的方法。在K-Means聚类的情况下，我们使用肘部法则来定义最佳的聚类数。什么是K-Means聚类中肘部法则？如我们所知，在k-means聚类算法中，我们随机初始化k个聚类，并且我们迭代地调整这k个聚类，直到这些k-质心处于平衡状态。然而，在初始化这些集群之前，我们要做的主要事情是确定我们必须使用多少个集群。
使用肘部法则确定K-Means中的k值
跟着大数据和AI去旅行
09-11 4804
现在，为了确定最佳的聚类数（k），我们绘制了k与它们的WCSS值的关系图。为了确定聚类的最佳数量，我们必须选择“弯头”处的k值，即distortion/inertia开始以线性方式减小的点。在这种方法中，为了确定k值，我们连续迭代k=1到k=n（这里n是我们根据要求选择的超参数）。下面我们将分4步实现肘部法则。首先，我们将创建随机数据集点，然后我们将在此数据集上应用k均值，并计算1到4之间的k的wcss值。我们将k的值从1迭代到n，并计算每个k值的Distortion，给定范围内每个k值的Inertia。
肘方法确定KMeans聚类的最佳K值
我的博客
08-28 3万+
当Kmeans聚类的K没有指定时，可以通过肘部法来估计聚类数量 K_means参数的最优解是以成本函数最小化为目标 成本函数为各个类畸变程度之和 每个类的畸变程度等于该类重心与其内部成员位置距离的平方和 但是平均畸变程度会随着K的增大先减小后增大，所以可以求出最小的平均畸变程度 import numpy as np import matplotlib.pyplot as plt fr...
【聚类】K-Means聚类（优缺点、手肘法、轮廓系数法、检测异常点、图像压缩，含代码实战）
学无止境、积少成多、厚积薄发
03-23 1万+
K-Means聚类（优缺点、手肘法、轮廓系数法、检测异常点、图像压缩，含代码实战）
肘部取值法 并给出应该选择k的大小
weixin_73824936的博客
11-08 1180
在K均值聚类中，"肘部取值法"是一种常用的方法，用于帮助选择最佳的聚类数量K。该方法涉及绘制不同K值下的聚类误差（通常是平方误差和）的图表，然后找出曲线出现拐点的位置，该拐点对应的K值通常被认为是最佳的选择。
k-means手肘法和轮廓系数
04-24
### K-Means算法中的手肘法与轮廓系数 #### 手肘法的作用 手肘法是一种用于确定K-Means聚类中最佳簇数量 \( k \) 的方法。该方法基于误差平方和（Sum of Squared Errors, SSE），即每个样本到其所属簇中心的距离平方和。当 \( k \) 小于真实聚类数时，随着 \( k \) 增加，SSE 会显著下降；然而，当 \( k \) 达到真实聚类数后，继续增加 \( k \) 对降低 SSE 的效果变得微乎其微[^4]。因此，在绘制 \( k \)-\( SSE \) 曲线时，曲线会出现类似于“手肘”的形状，其中弯曲处对应的 \( k \) 即为最优簇数。 #### 轮廓系数的作用 轮廓系数则提供了一种更全面的方法来评估聚类质量。它综合考虑了簇内紧密性和簇间分离度两个方面。具体而言，对于每一个数据点，计算其与同簇其他点的平均距离（簇内距离）以及与其他最近簇的平均距离（簇间距离）。通过这两个指标，可以得到单个点的轮廓值，范围介于 -1 到 1 之间。较高的轮廓值表示更好的聚类效果，意味着簇内的紧凑性高且簇间的区分明显[^2]。 #### 手肘法与轮廓系数的区别 | **对比维度** | **手肘法** | **轮廓系数** | |----------------------|-----------------------------------------------------------------------------------------------|---------------------------------------------------------------------------------------------| | **核心原理** | 基于 SSE 随着 \( k \) 变化的趋势分析 | 综合评价簇内紧致性和簇间分离度 | | **适用场景** | 更适合初步估计 \( k \)，尤其是在数据分布较为简单的情况下 | 提供更为精细的质量评估，适用于复杂数据结构 | | **优缺点** | 计算简便快速，但可能受噪声影响较大 | 结果更加可靠，但在大规模数据集上的计算成本较高 | | **输出形式** | 返回单一的最佳 \( k \) | 输出每一点的具体评分，可进一步挖掘局部异常 | 以下是两种方法的一个实现示例： ```python from sklearn.cluster import KMeans from sklearn.metrics import silhouette_score import matplotlib.pyplot as plt import numpy as np # 数据准备 data = np.random.rand(100, 2) # 使用手肘法寻找最佳k值 sse = [] for k in range(1, 11): kmeans = KMeans(n_clusters=k, random_state=42).fit(data) sse.append(kmeans.inertia_) plt.plot(range(1, 11), sse, marker='o') plt.title('Elbow Method') plt.xlabel('Number of clusters (k)') plt.ylabel('SSE') plt.show() # 使用轮廓系数验证最佳k值 sil_scores = [] for k in range(2, 11): # 至少需要2个簇才能计算轮廓系数 kmeans = KMeans(n_clusters=k, random_state=42).fit(data) score = silhouette_score(data, kmeans.labels_) sil_scores.append(score) best_k_silhouette = np.argmax(sil_scores) + 2 # 加2是因为range从2开始 print(f"Best k by Silhouette Score: {best_k_silhouette}") ``` #### 总结 尽管两者都旨在优化 K-Means 中的 \( k \) 参数选择，但它们各有侧重：手肘法依赖全局 SSE 下降的趋势，操作直观易懂；而轮廓系数深入考察个体层面的归属合理性，从而得出更具说服力的结果。实际应用中可根据需求灵活选用或联合运用这两种技术。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

东木月

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值