HDU 1012 u Calculate e

u Calculate e

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 38088    Accepted Submission(s): 17259

Problem Description

A simple mathematical formula for e is



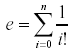
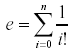
where n is allowed to go to infinity. This can actually yield very accurate approximations of e using relatively small values of n.

 

Output

Output the approximations of e generated by the above formula for the values of n from 0 to 9. The beginning of your output should appear similar to that shown below.

 

Sample Output

  
  

   
   n e
- -----------
0 1
1 2
2 2.5
3 2.666666667
4 2.708333333
  
  

分析：

这个题是一个水题，可是一开始却WA了3次，不明白问题在哪，后台拷贝别人代码，比较数据发现在n=8的时候发现有不同。

按输出示例来看，保留9位小数，但是末尾无效的0需要抹去，所以我一开始用的%g输出（抹掉小数点后无效的0），第8组数据e的答案是2.718278770，用%g自然抹去了末尾的0，本以为是题目评判的的BUG，

后来多输出几位之后发现，该‘0’是由于四舍五入出现的，所以是有效的‘0’，所以不应该抹去。

下面是代码：

错误代码：

#include <stdio.h>
int main()
{
	int i,n,sum[12];
	double e=1.;
	printf("n e\n- -----------\n0 1\n");
	sum[0]=1;
	for(n=1;n<=9;n++)
	{
		sum[n]=sum[n-1]*n;
		e=e+1.0/sum[n];
		printf("%d %.10g\n",n,e);
	}
	
	return 0;
}

正确代码：

#include <stdio.h>
int main()
{
	int i,n,sum[12];
	double e=2.5;
	printf("n e\n- -----------\n0 1\n1 2\n2 2.5\n");
	sum[2]=2;
	for(n=3;n<=9;n++)
	{
		sum[n]=sum[n-1]*n;
		e=e+1.0/sum[n];
		printf("%d %.9lf\n",n,e);
	}
	
	return 0;
}