数据结构学习笔记分享

一、线性表

1. 概念

线性表是n个相同的数据类型元素组成的有限序列。

线性表包括顺序表和链表。

2. 特点

线性表中元素的个数n就是线性表的长度，n = 0时为空表。

对于非空线性表，有如下特点：

存在头节点和尾节点；

除了头节点外，结构中的每一个元素都只有一个前驱；

除了尾节点外，结构中的每一个元素都至于一个后继。

3. 顺序表

用一组连续的存储单元依次存储线性表的各个元素。也就是说，逻辑上相邻的元素，实际的物理空间也是连续的。

优点：访问速度快、存储密度高（数据连续存储，无需额外空间存放指针）、尾部操作快

缺点：插入/删除慢、长度固定、扩容正本高

总结：顺序表适合 “读多写少”、需要随机访问的场景，如数组、缓冲区。

4. 链表

用一组任意的存储单元存储线性表的各个元素。（这组存储单元可以是连续的，也可以不连续）

链表适合适合 “写多读少”、动态变化的场景

单链表

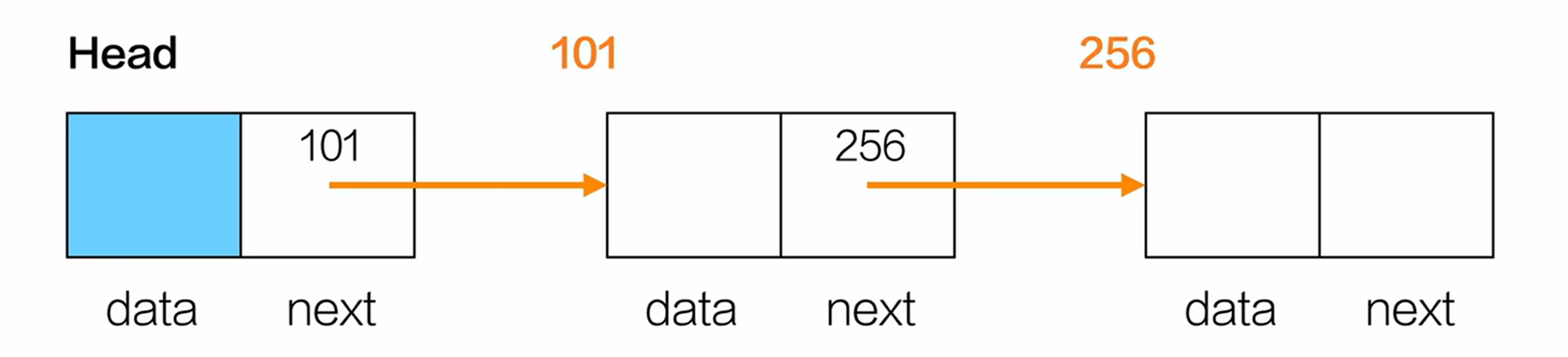
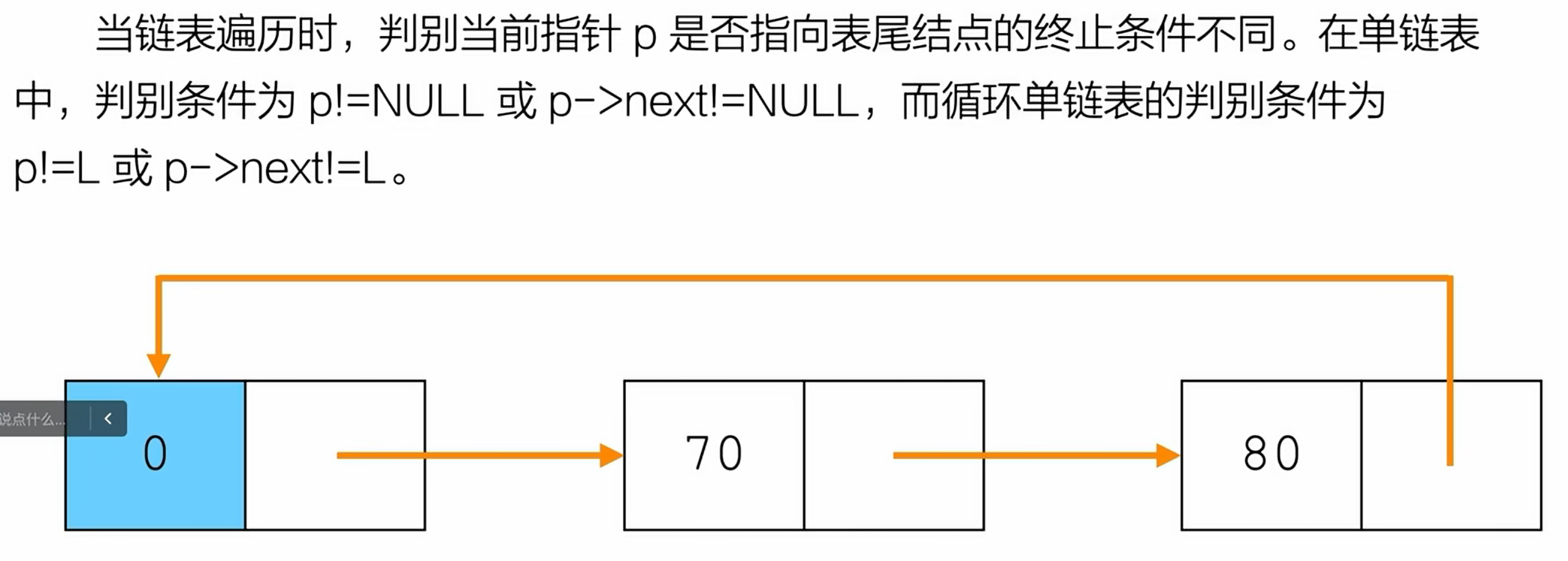
单向循环链表

特点是表中最后一个节点的指针域指向头节点，整个链表形成一个环。

双向链表

双向链表的节点中有两个指针域，一个指向直接后继，另一个指向直接前驱。

5. 栈

栈，是仅在表尾进行插入或删除操作的线性表。

表尾称栈顶，表头称栈底，不含元素称空栈。

栈是后进先出！

顺序栈

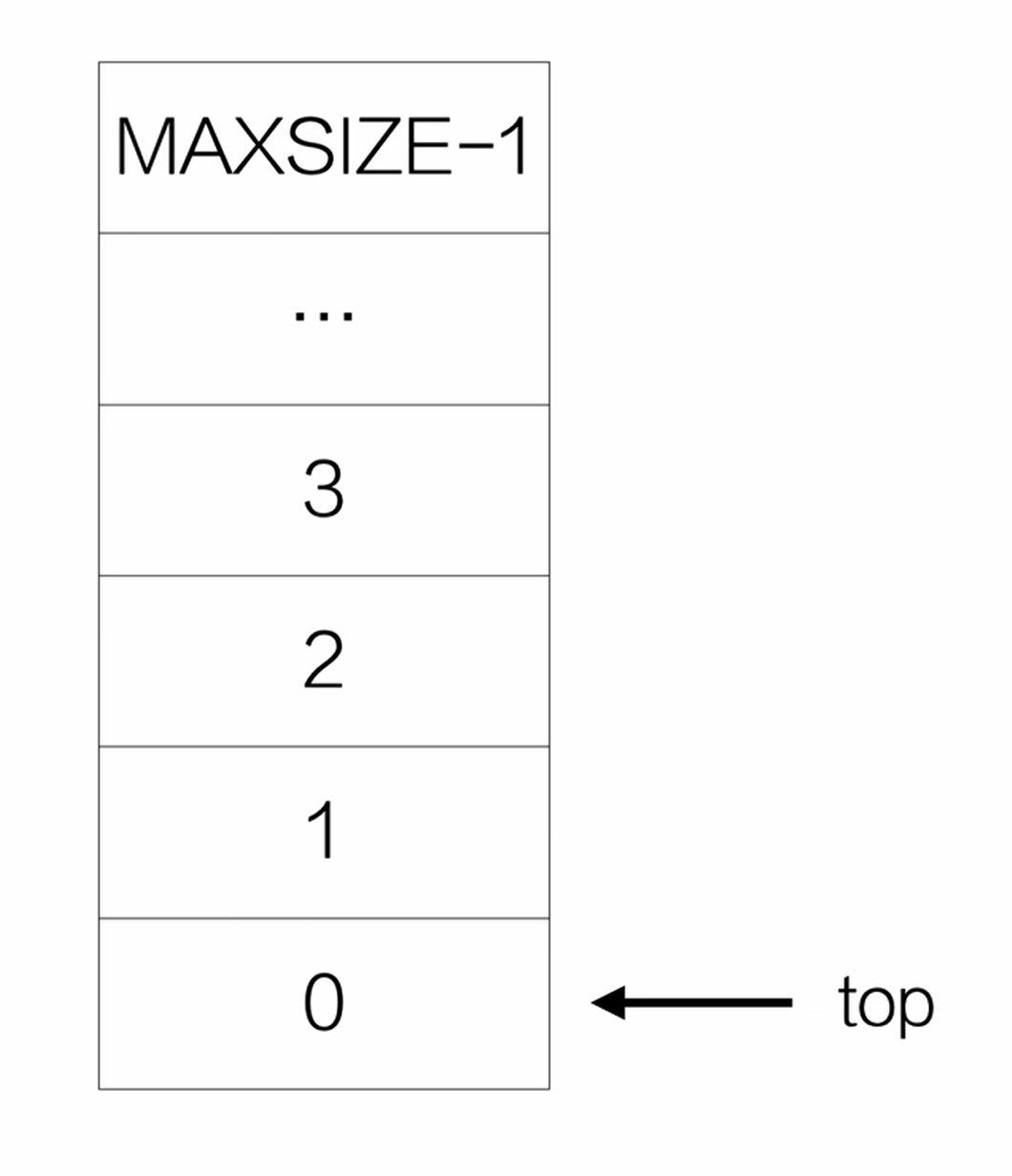
链栈

无论什么栈，搞清楚栈顶在哪很重要，然后再进行其他操作！

6. 队列

队列是一种先进先出的线性表。只允许在表的一端插入，在另一端删除元素。

插入的一端叫队尾(rear)，删除的一端叫队头(front)。

顺序队

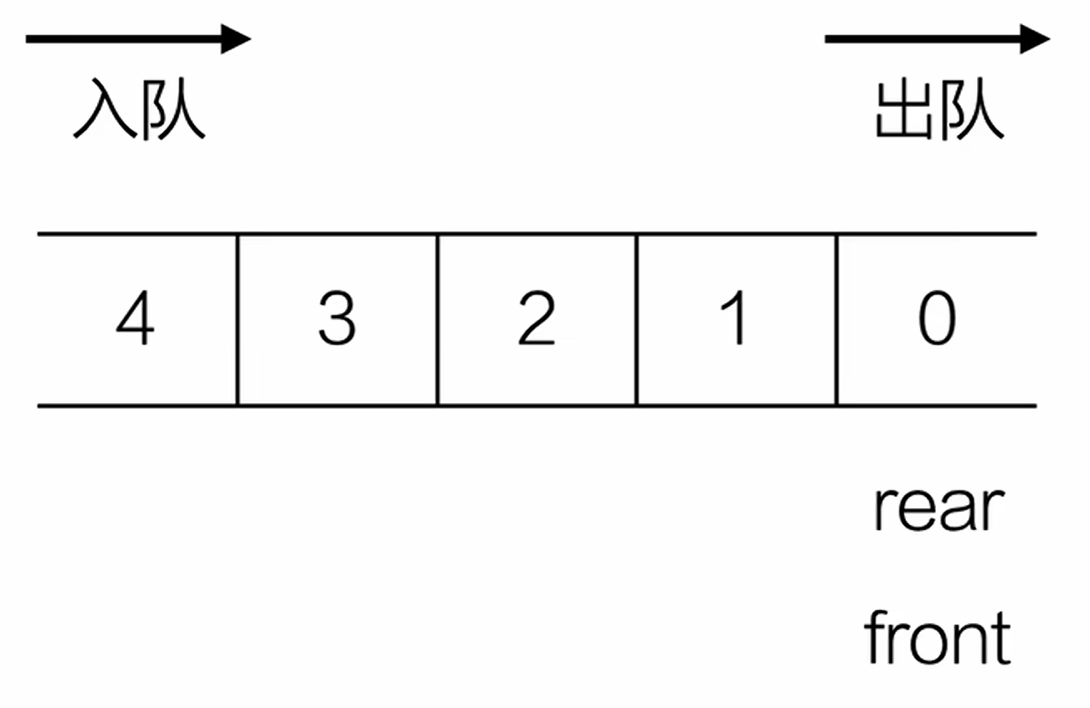
循环队

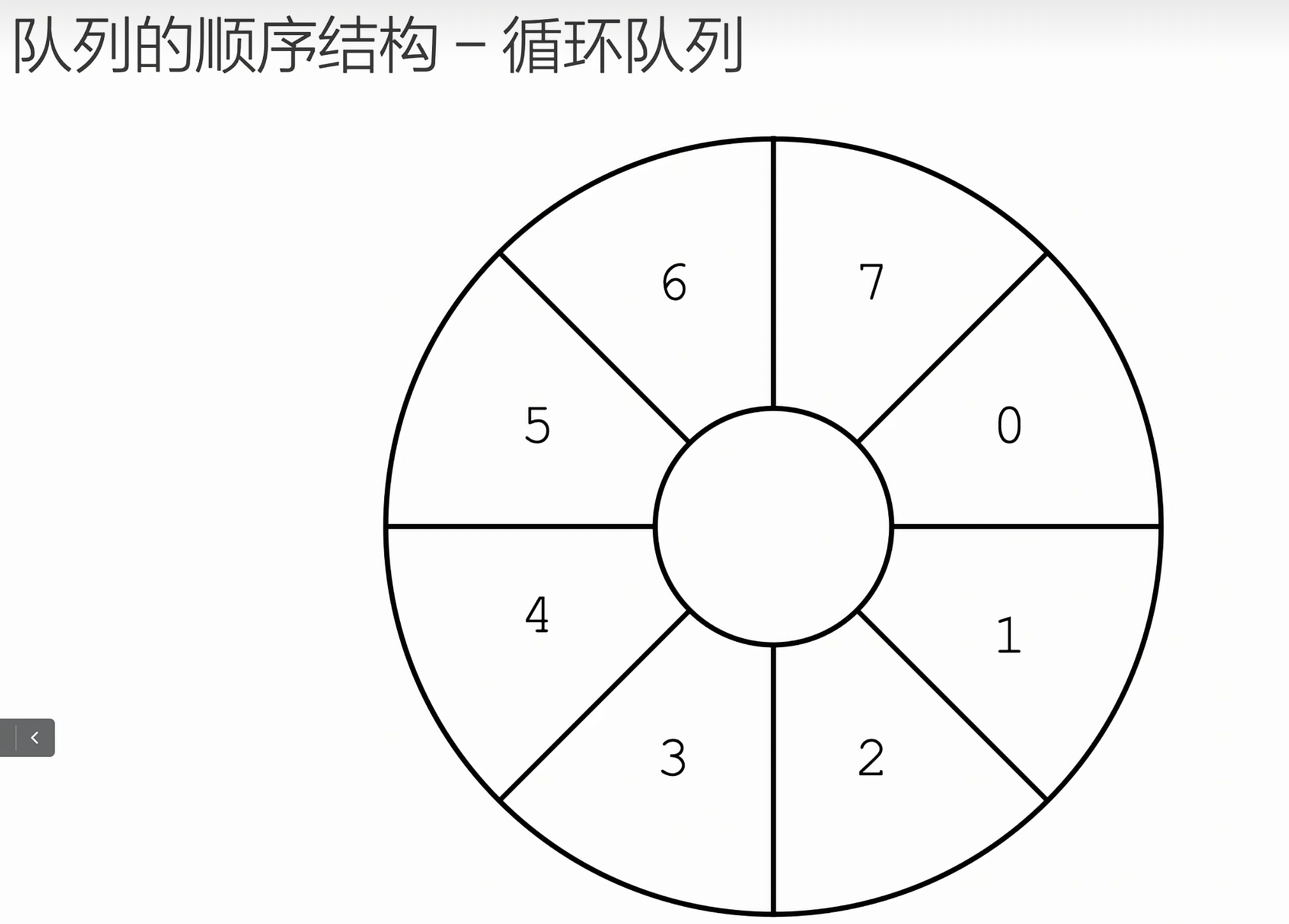
链队

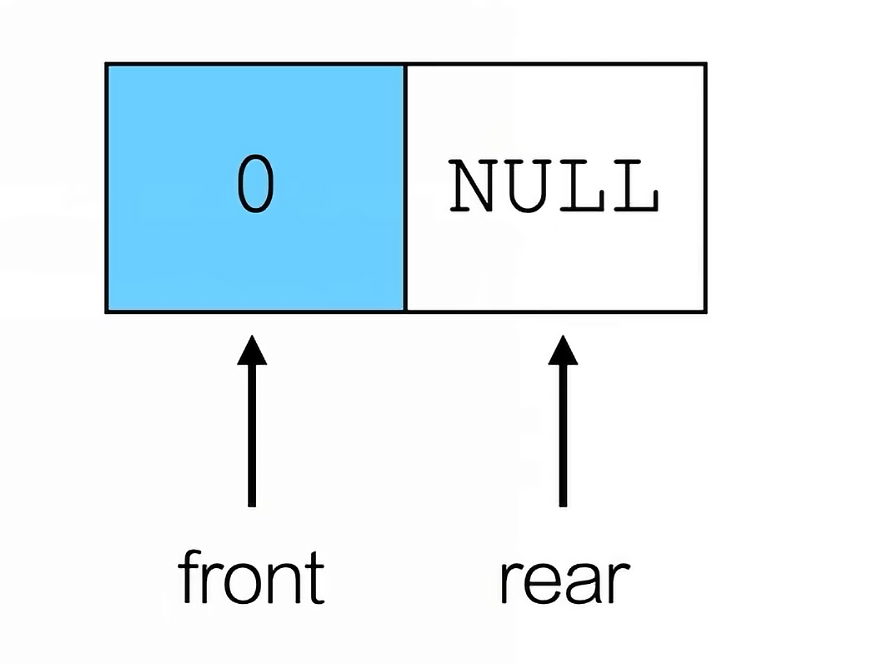
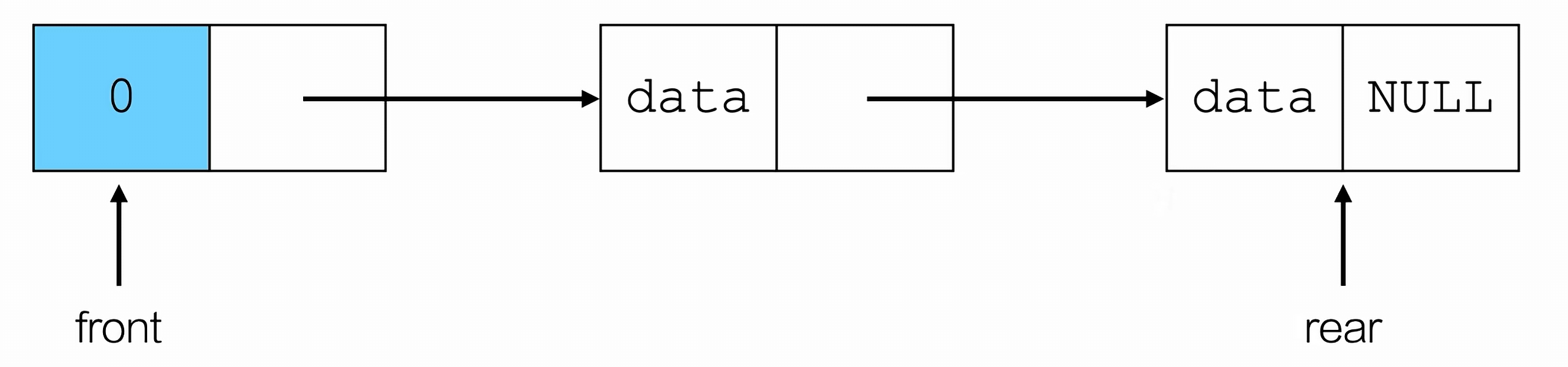
二、树

1. 概念

树是一个或多个结点的有限集合。

存在一个称为根的特定结点。

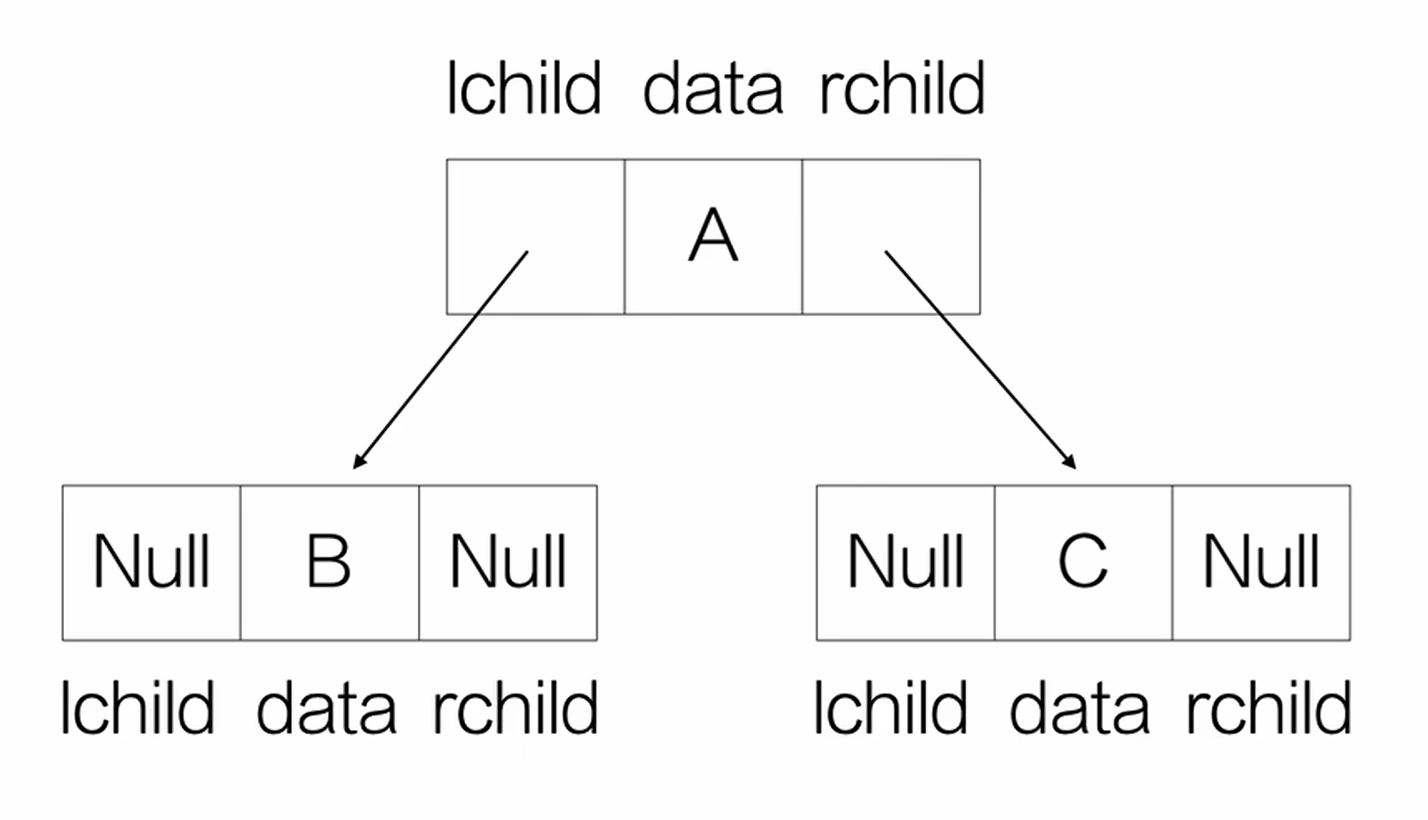
A是根节点，BCD是A的子树。

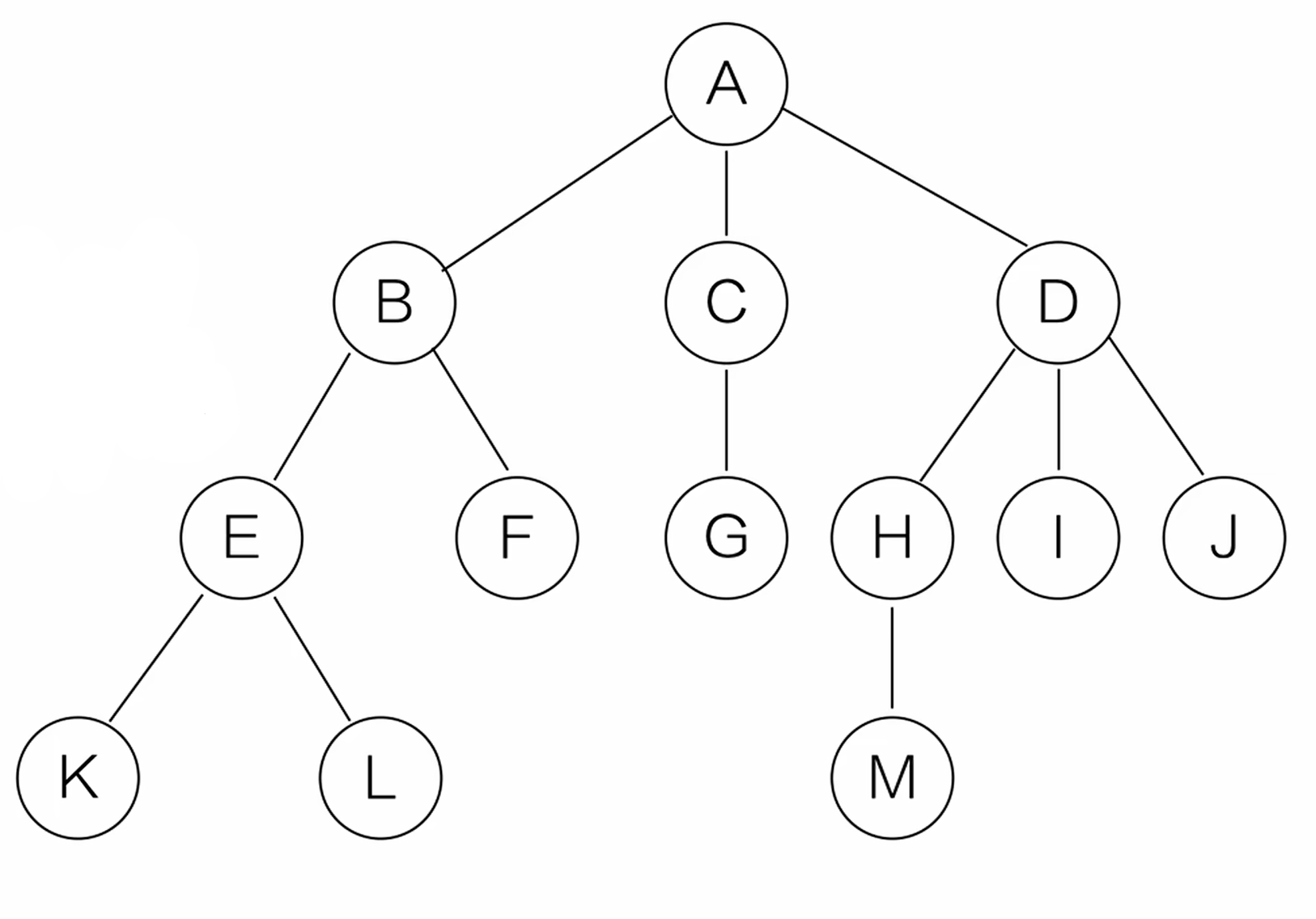
结点：树中的一个独立单元。

结点的度：结点拥有的子树数量称为结点的度。（A节点有3个子树，那么有3个度）

树的度：树内各结点度的最大值。

叶子结点(终端结点)：度为0的结点。

非终端结点：度不为0的结点。

双亲和孩子：结点子树的根称为孩子，该结点称为孩子的双亲。（A的孩子是BCD）

层次：结点的层次从根开始定义。根结点为第一层，以此类推。

2. 二叉树

二叉树是n(n>=0)个jiedian所构成的集合，它或为空树或为非空树。

非空树：就是每个结点至多只有2个子树，且子树有左右之分，次序不能颠倒。

二叉树的性质

完全二叉树：没有左子树(要完整)，不能有右子树；上一层没有铺满，不能有下一层。

顺序二叉树

链式二叉树

前序遍历

根节点→左子树→右子树

中序遍历

左子树→根节点→右子树

后序遍历

左子树→右子树→根节点

已知前中遍历，中后遍历，可以画出一颗二叉树

3. 哈夫曼树

基本概念

路径：从树中一个结点到另一个结点之间的分支构成这两个结点之间的路径

路径长度：路径上的分支数目

树的路径长度：从树根到每一个结点的路径长度之和（1*2+2*4+3*2）

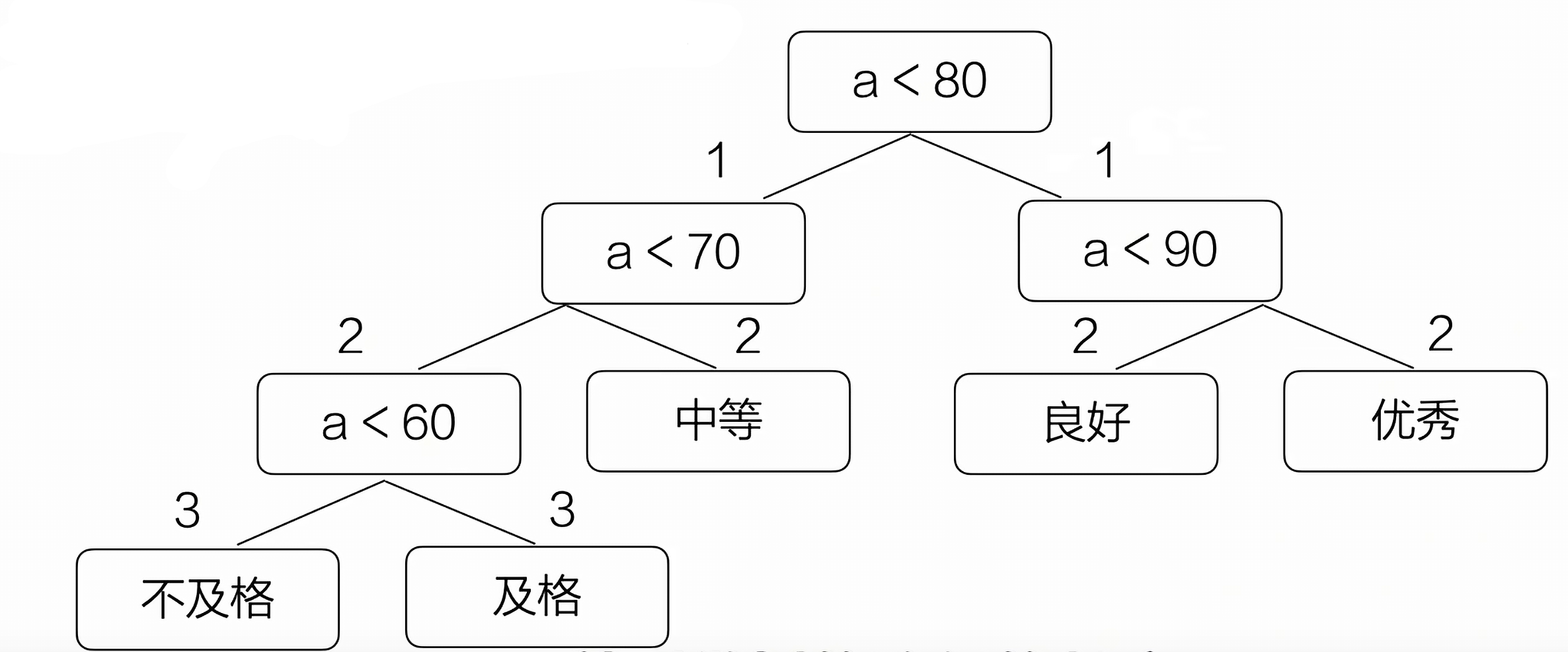
结点的权：在实际应用中，给树中的结点赋予代表某种含义的数值

结点的带权路径长度：从该结点到树根之间的路径长度与其权的乘积

树的带权路径长度(WPL)：树中的所有叶子结点的带权路径长度之和

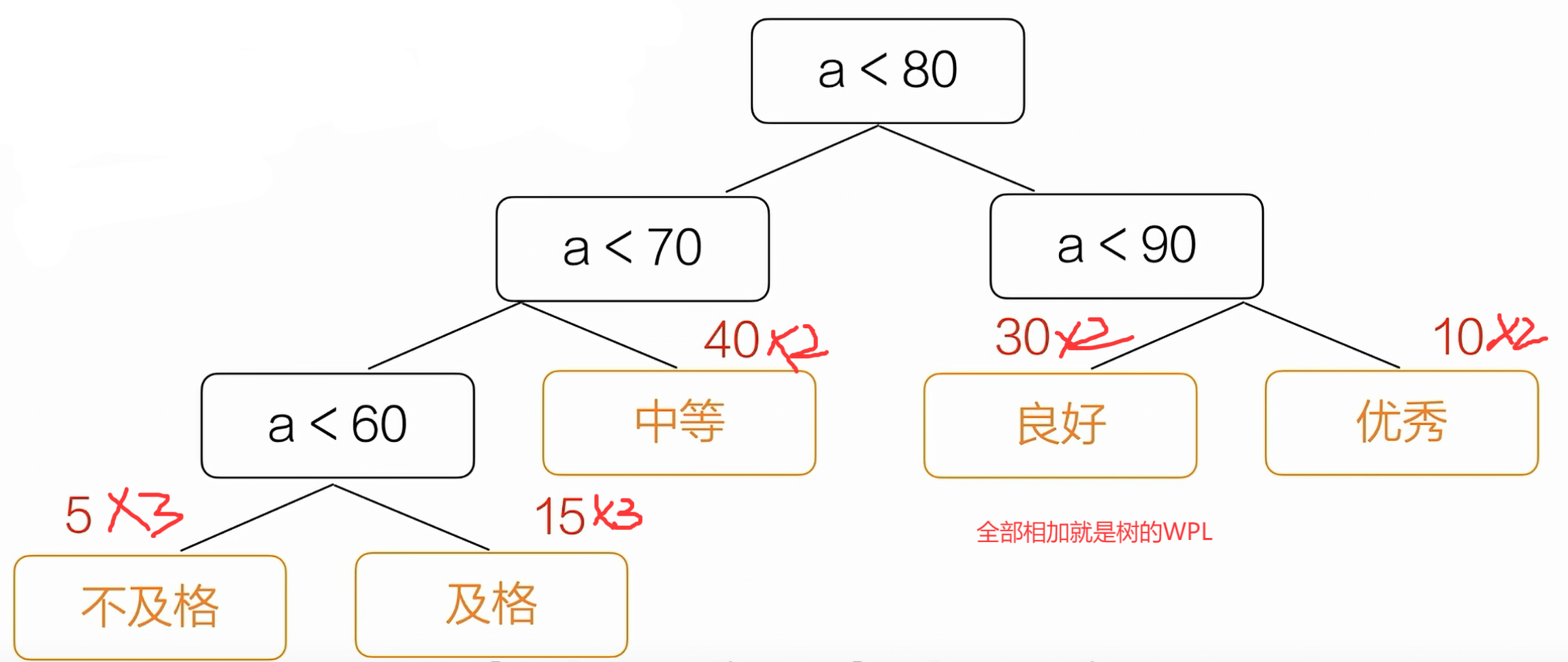
定义

带权路径长度WPL最小的二叉树称为哈夫曼树。

构造哈夫曼树

（1）先把有权值的叶子结点按照从小到大的顺序排列成一个有序序列。

（2）选两个最小权值的结点作为新结点N1的子结点。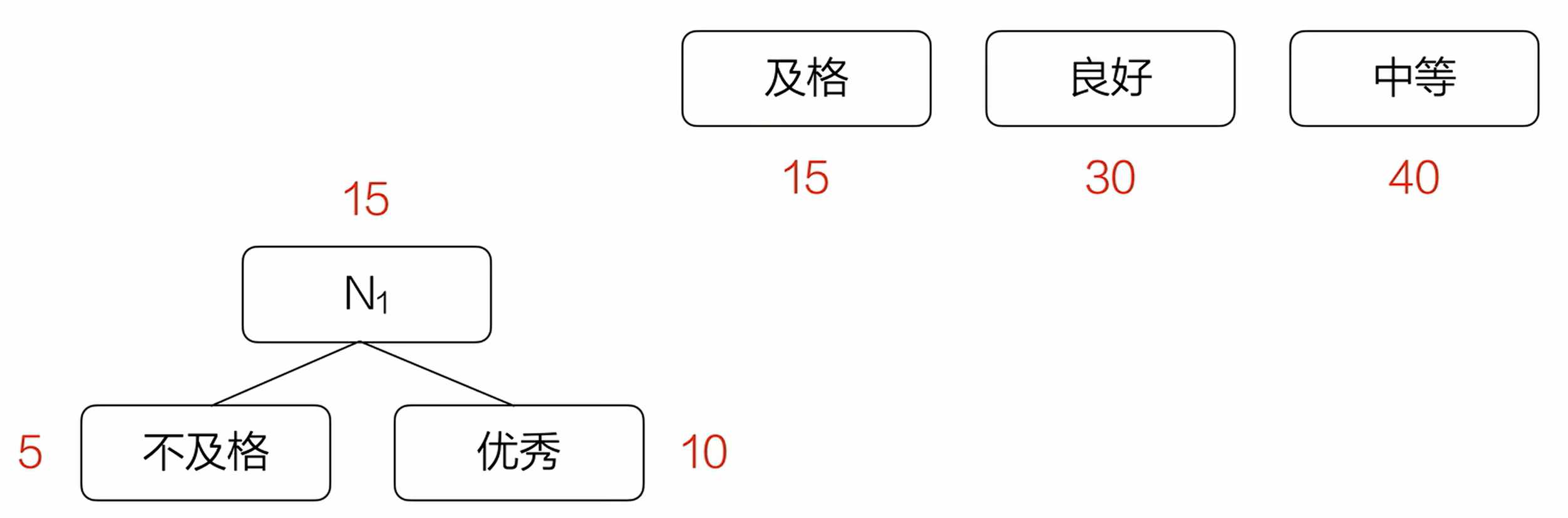

（3）将结点N1替换取出的结点，并入有序序列。

（4）重复步骤（2），将N1和及格作为N2的子结点。

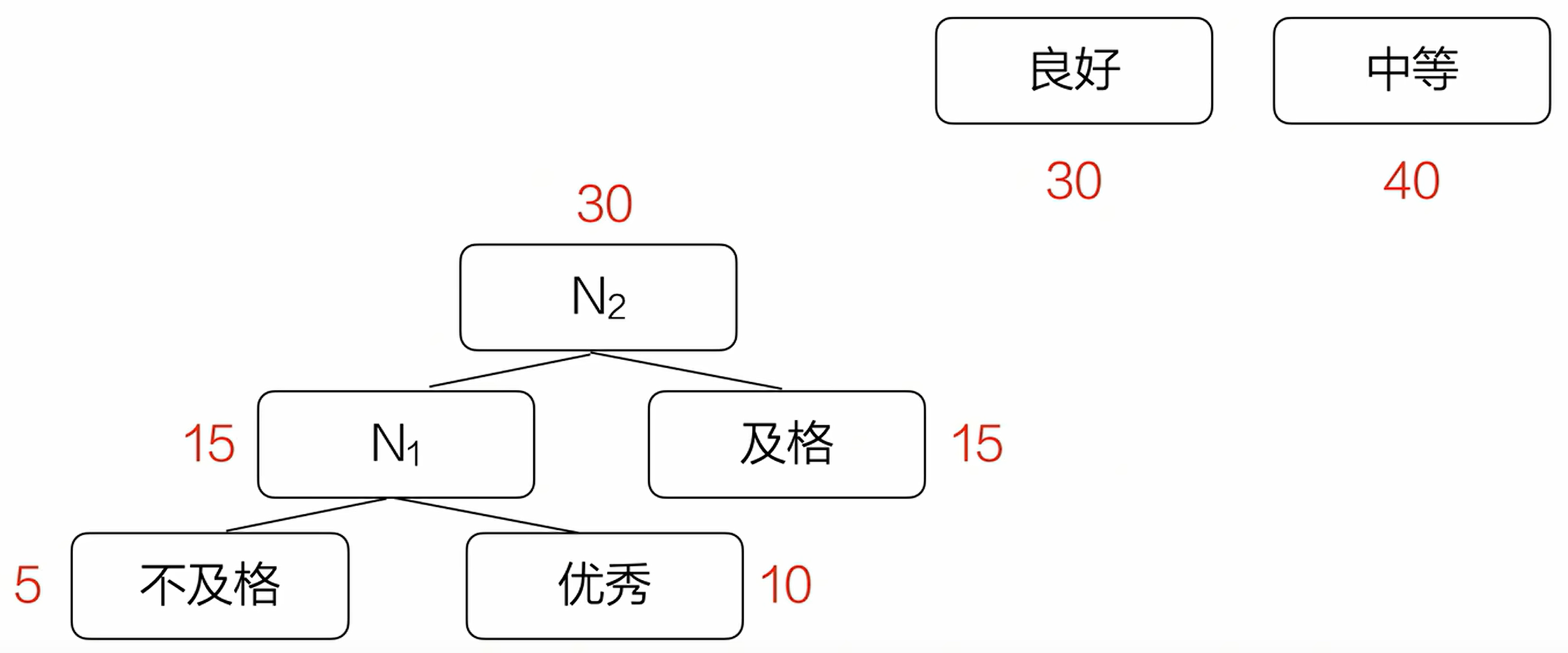
（5）重复步骤（3），拿回去接着排。

（6）重复步骤2、3，直到完成哈夫曼树的构造。

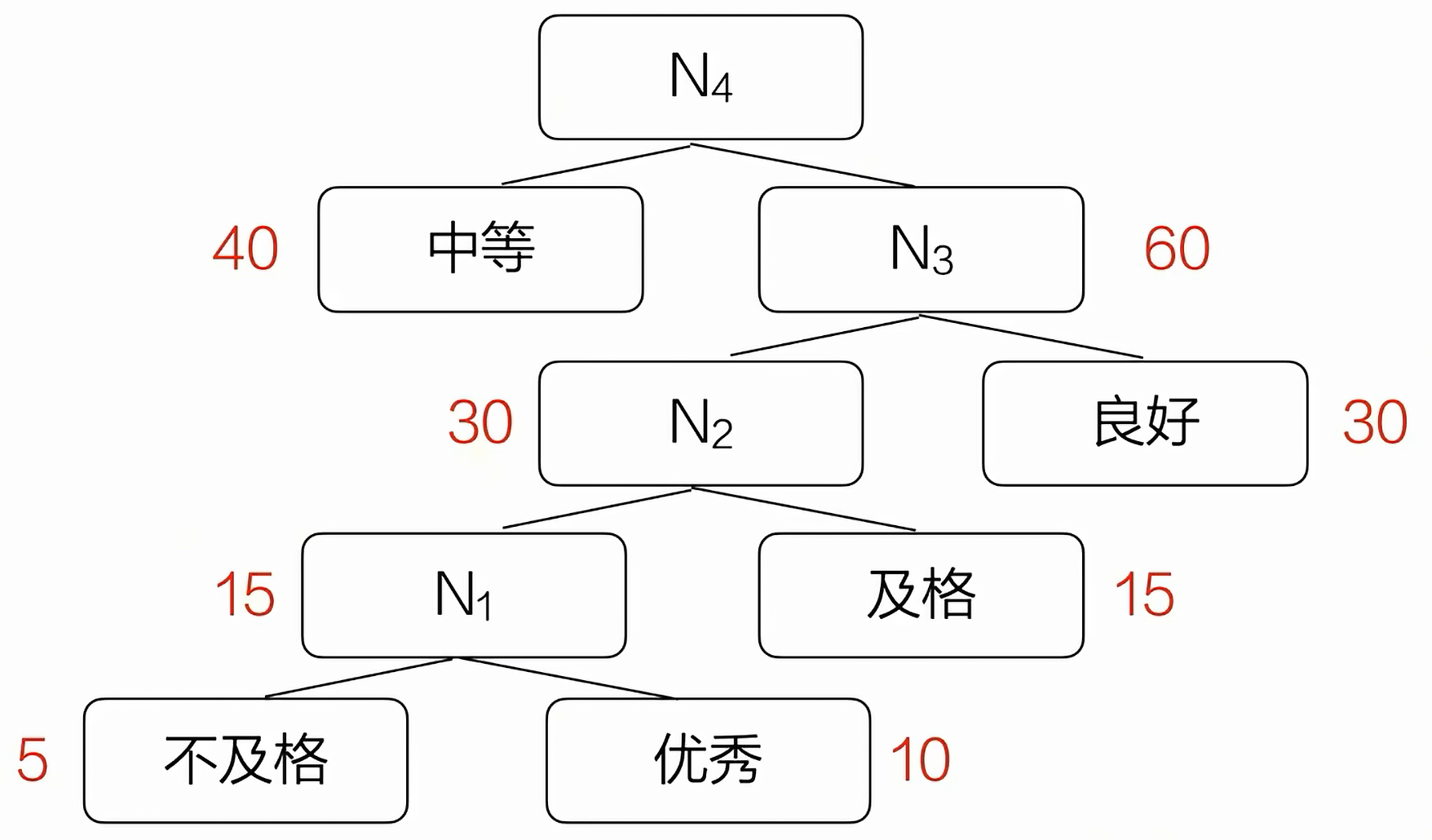
WPL = 40*1+30*2+15*3+5*4+10*4 = 205

4. 树与二叉树的转换

树转二叉树（先连兄弟，再断原右孩子，最后转）

（1）加线。在所有兄弟结点之间加一条线

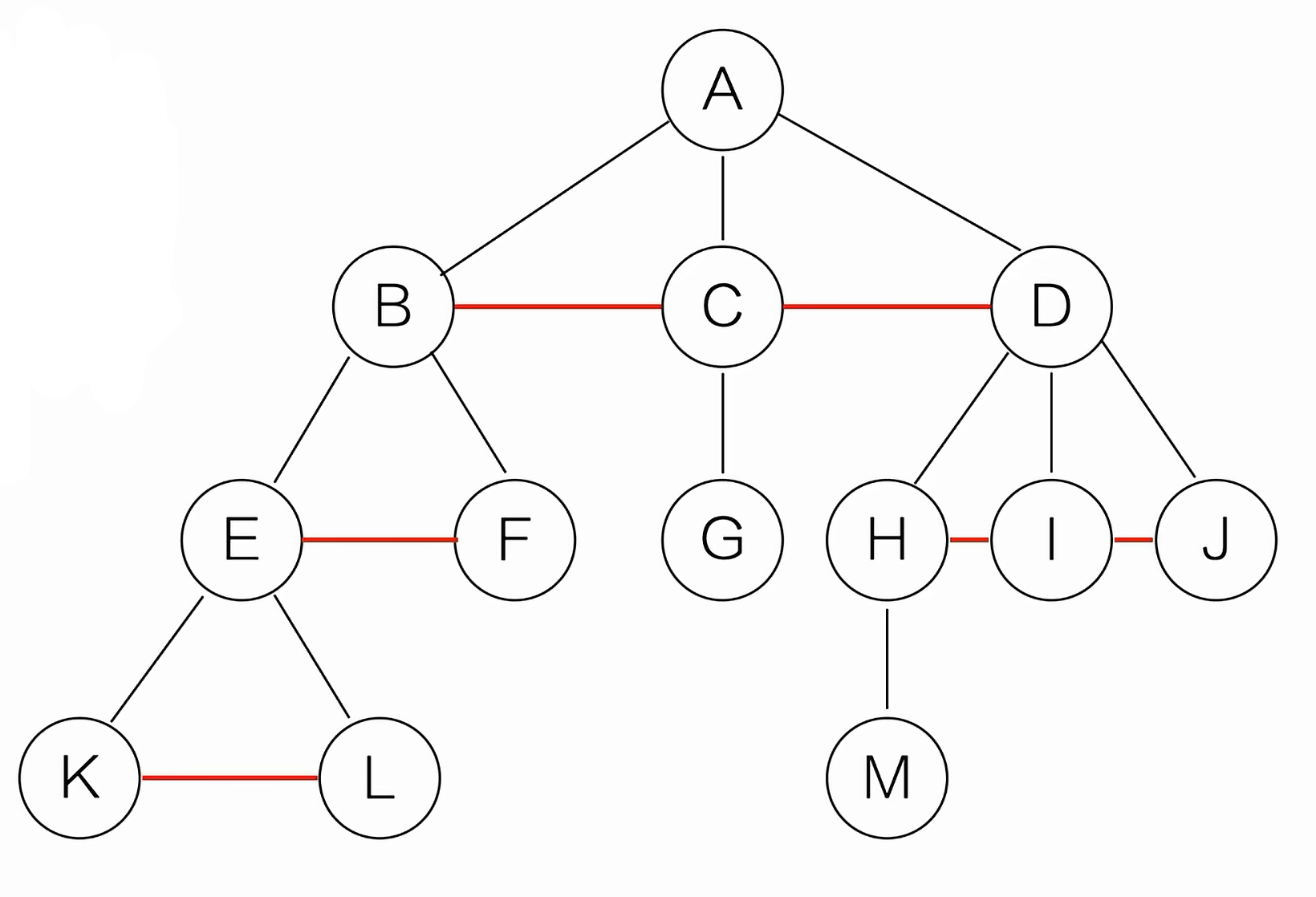
（2）去线。对树中的每一个结点，只保留它与第一个孩子结点的连线，删除它与其他孩子的连线

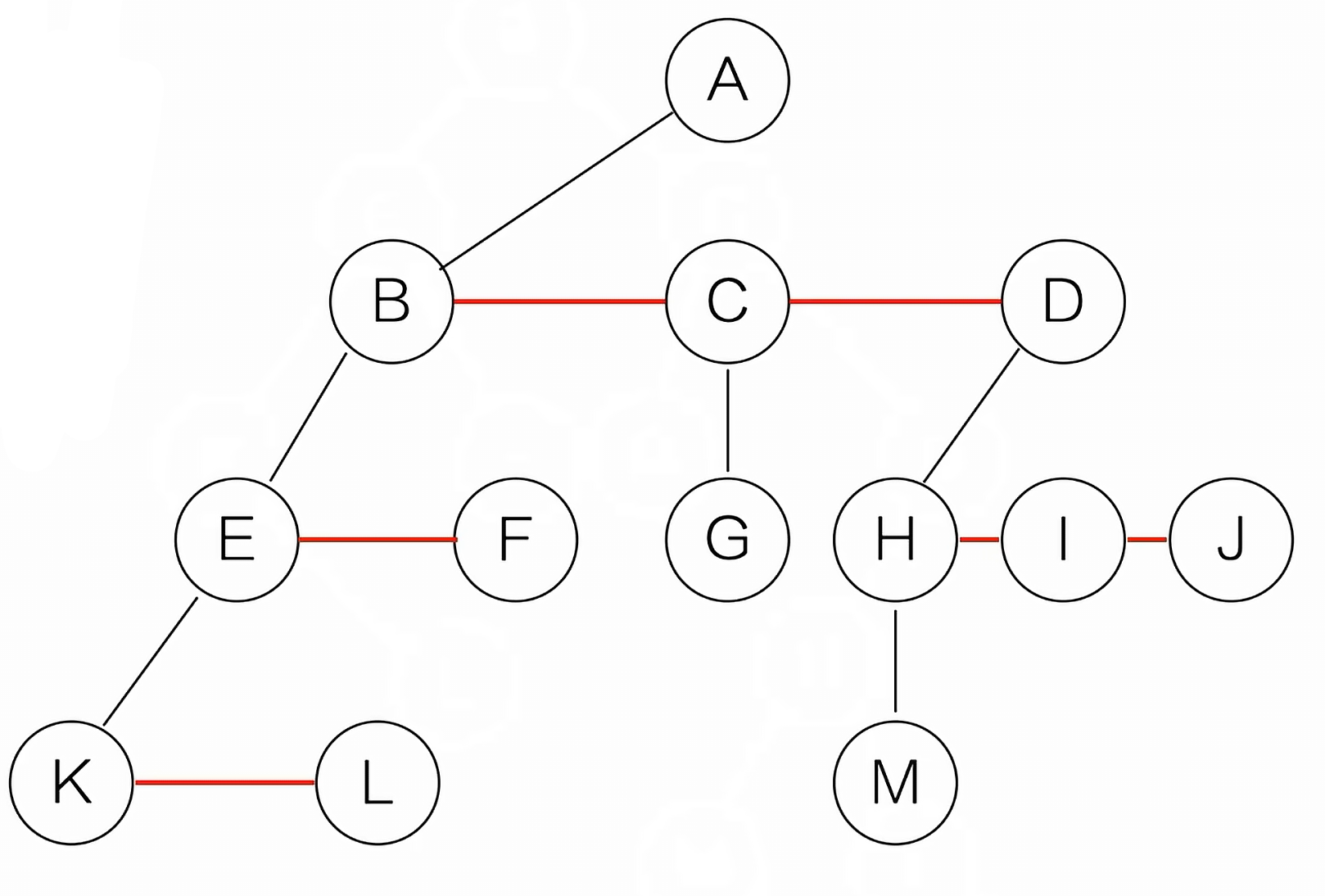
（3）层次调整。以树的根节点为轴心，将整棵树顺时针旋转一定角度，使之层次分明。注意：第一个孩子是二叉树孩子的左孩子。兄弟转过来的孩子是结点的右孩子（例如J转过来是I的右孩子）。

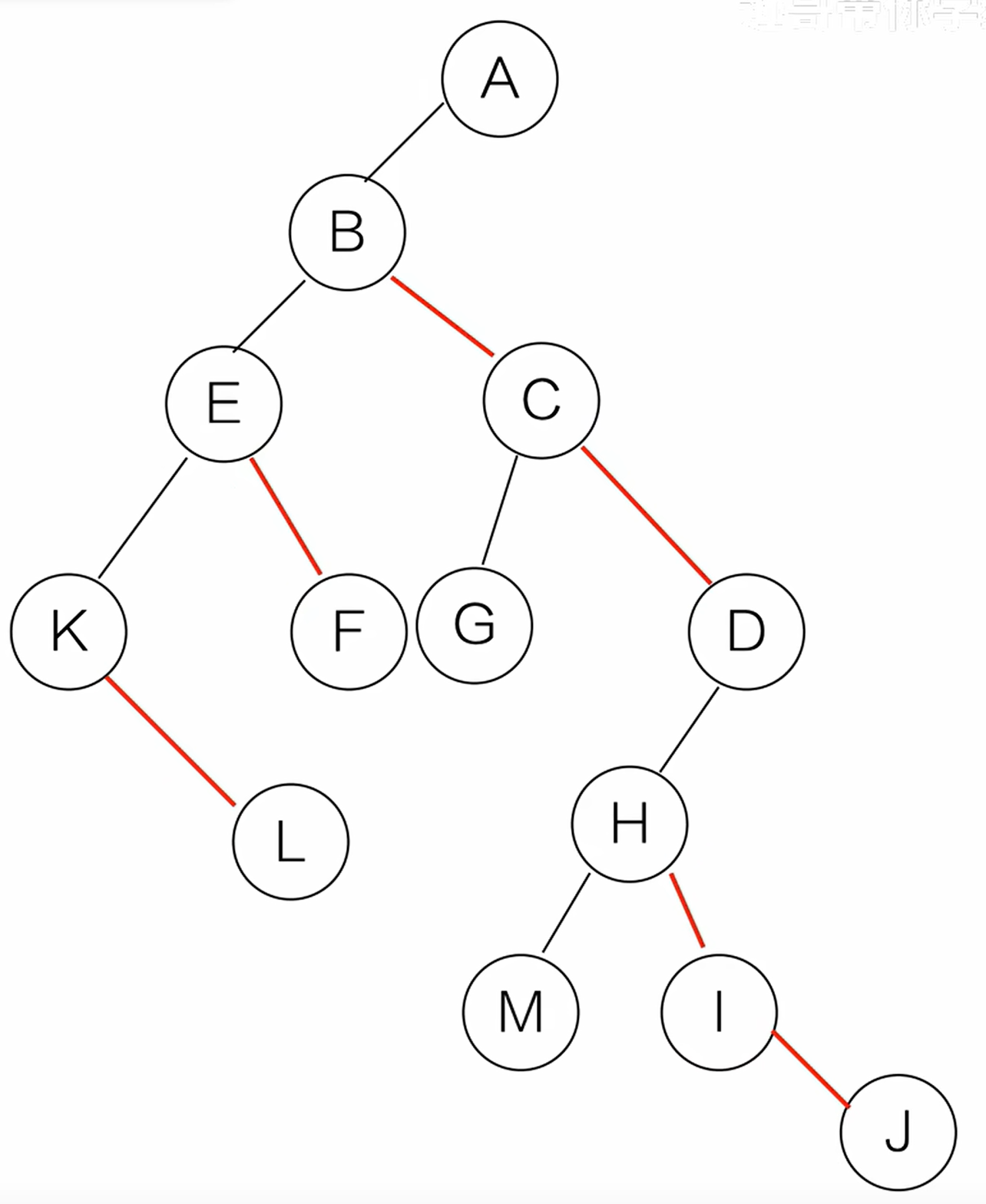
二叉树转树（先结点连有左孩子的右孩子，再断原右孩子，最后调整）

（1）加线，若某个结点有左孩子，则将该左孩子的所有右孩子也作为该父结点的孩子并连接起来

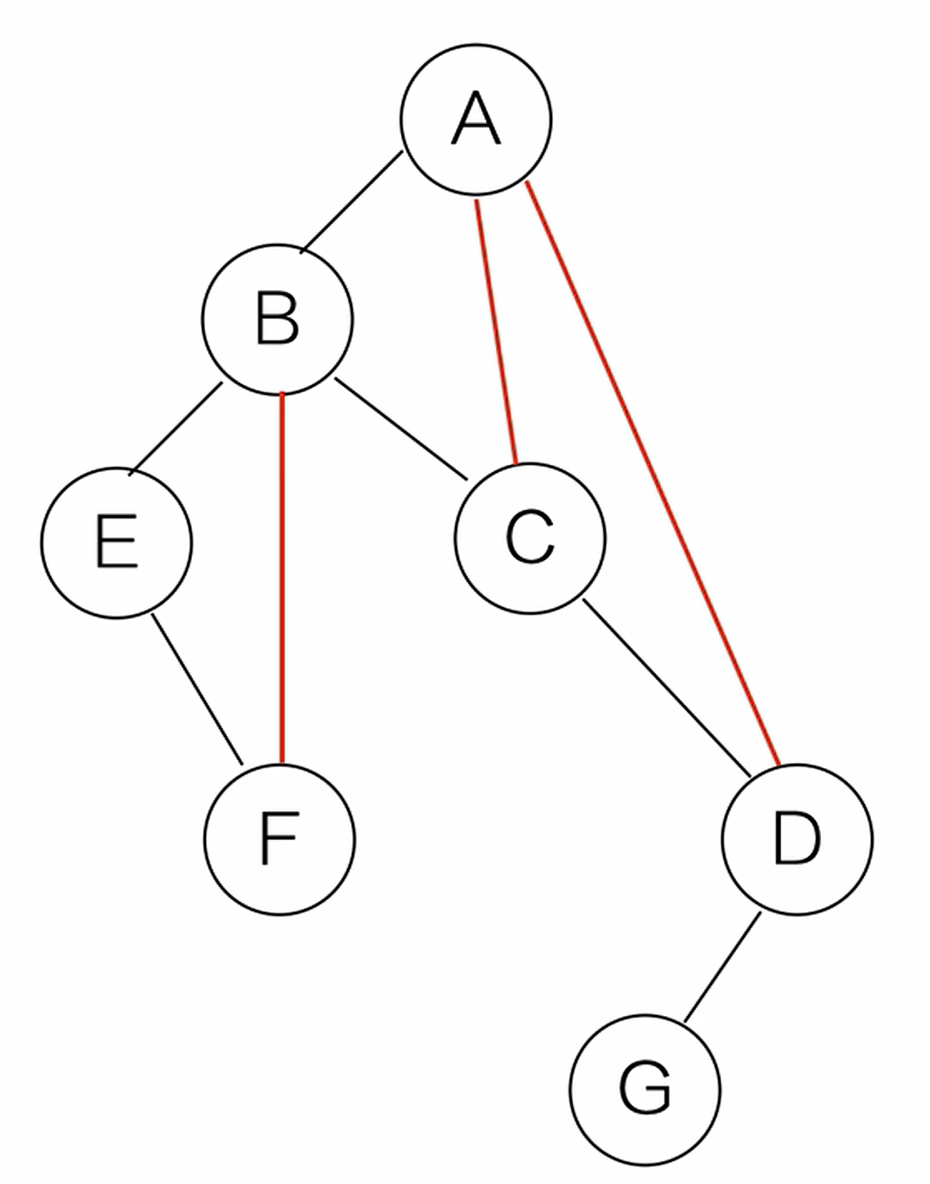
（2）去线。删除原二叉树中所有结点与其右孩子的连线

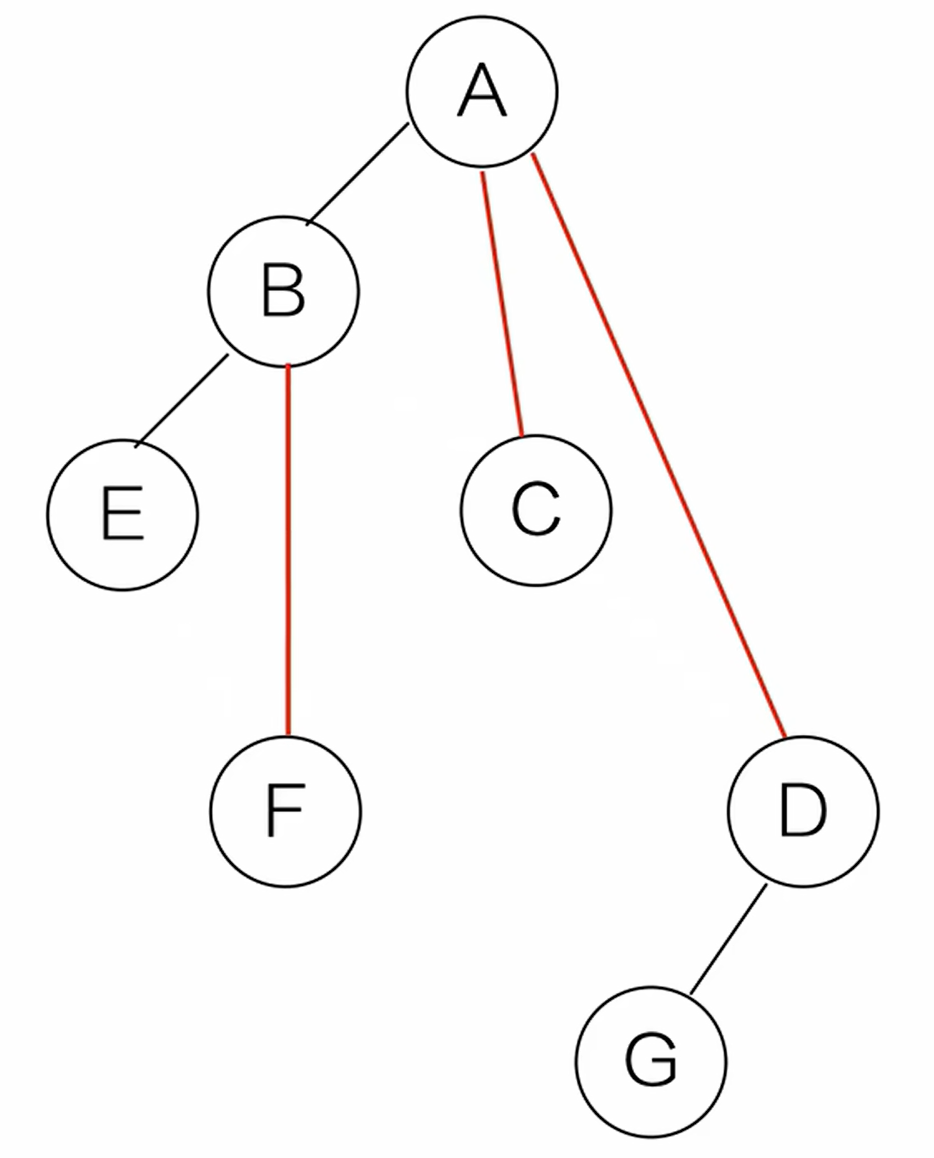
（3）层次调整

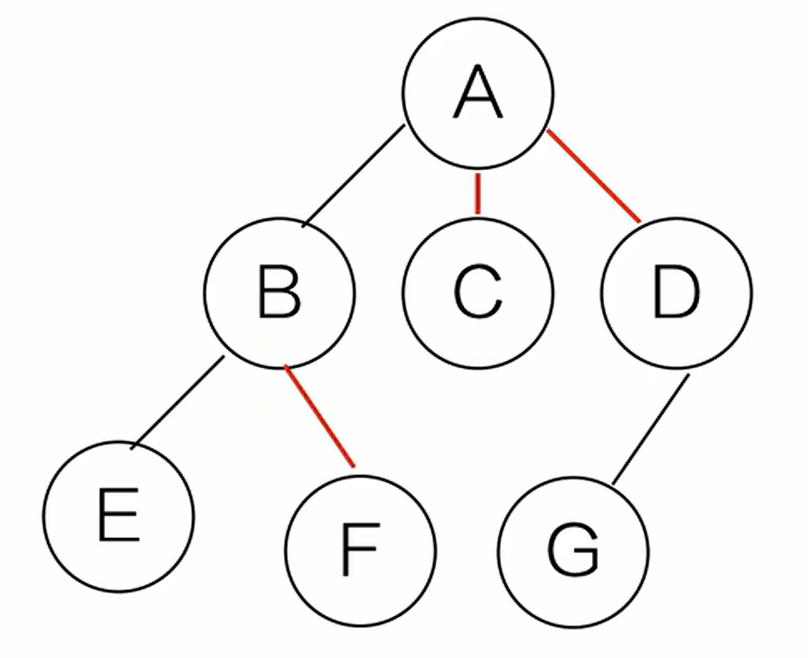
5. 森林与二叉树的转换

森林转二叉树

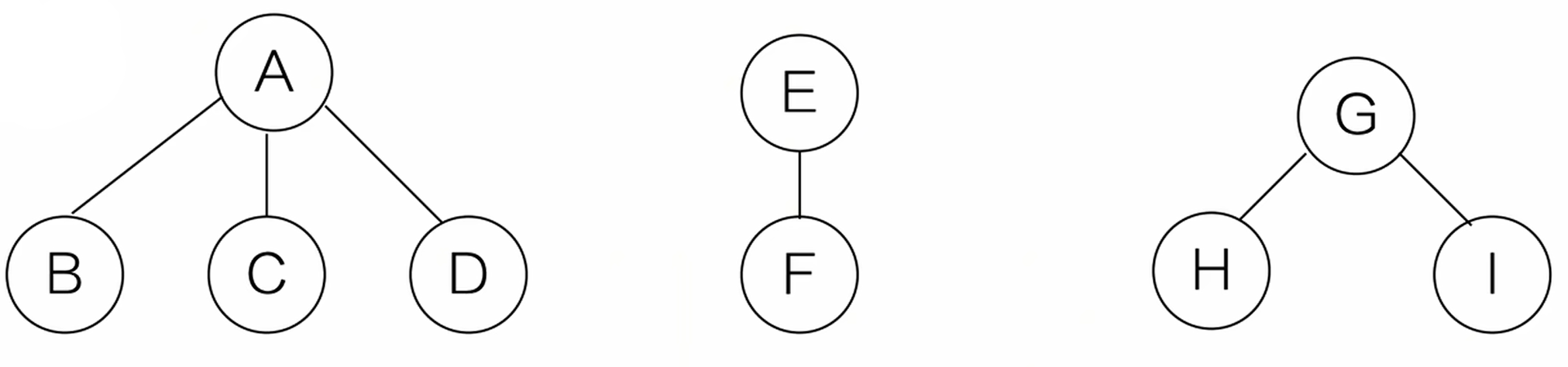
（1）先把树转换成二叉树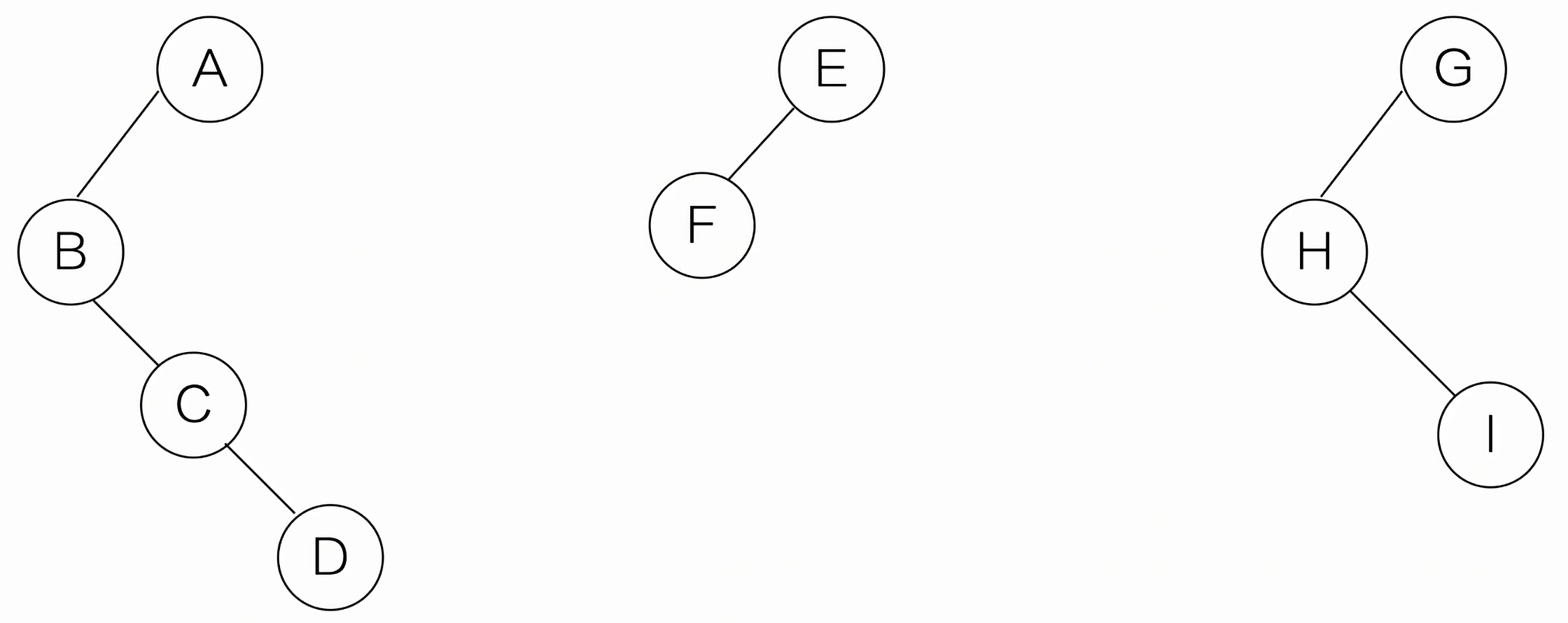

（2）第一课二叉树不动，从第二课树开始，依次把后一颗二叉树的根结点作为前一课二叉树的根节点的右孩子，然后用线连起来

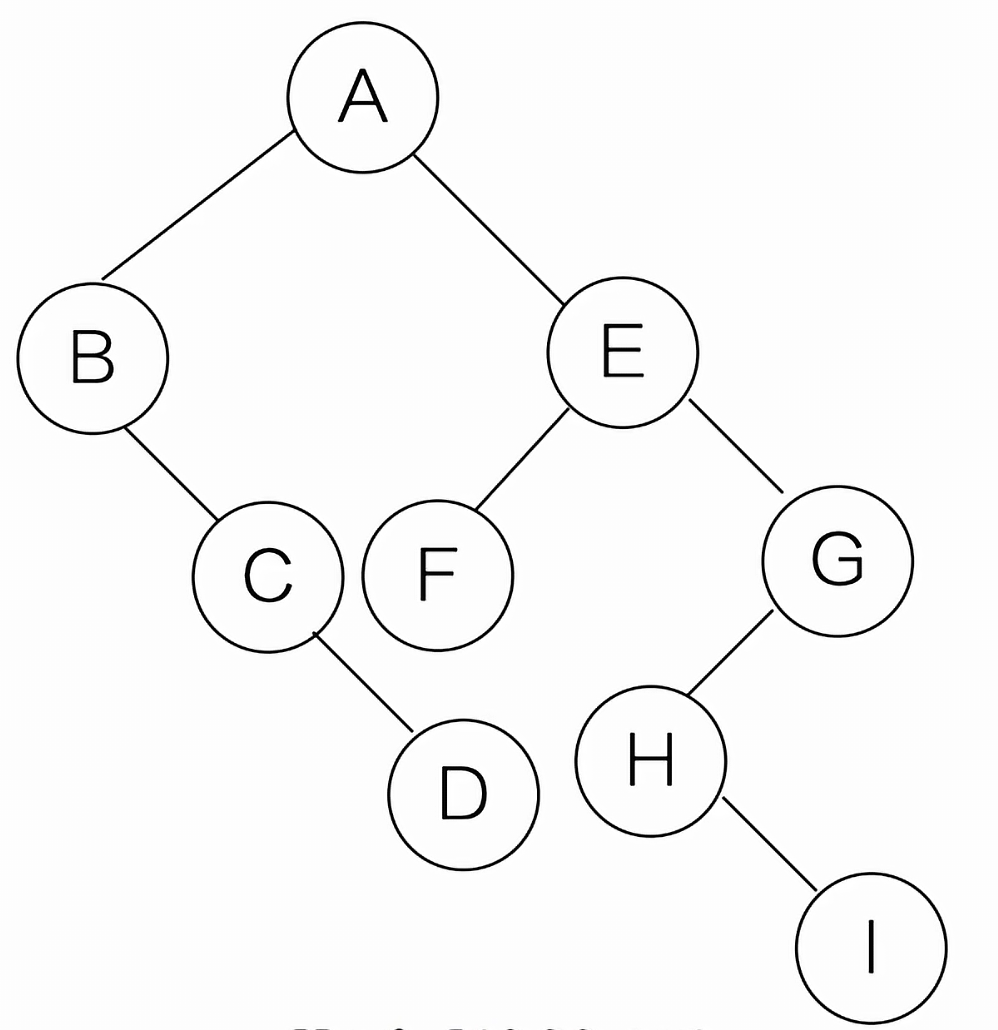
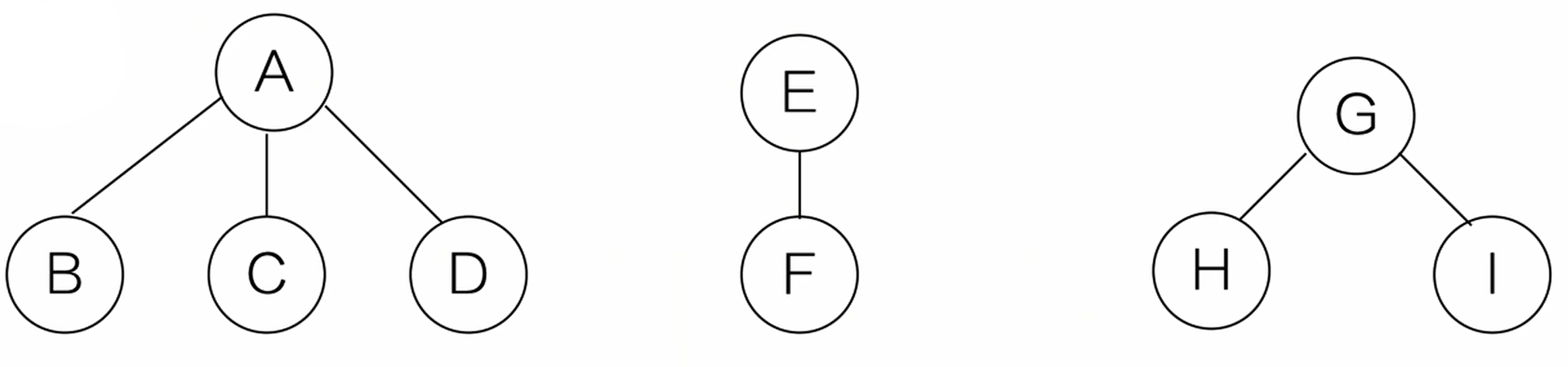
二叉树转森林

（1）去线。从根结点开始，若右孩子存在，则把右孩子结点的连线删除

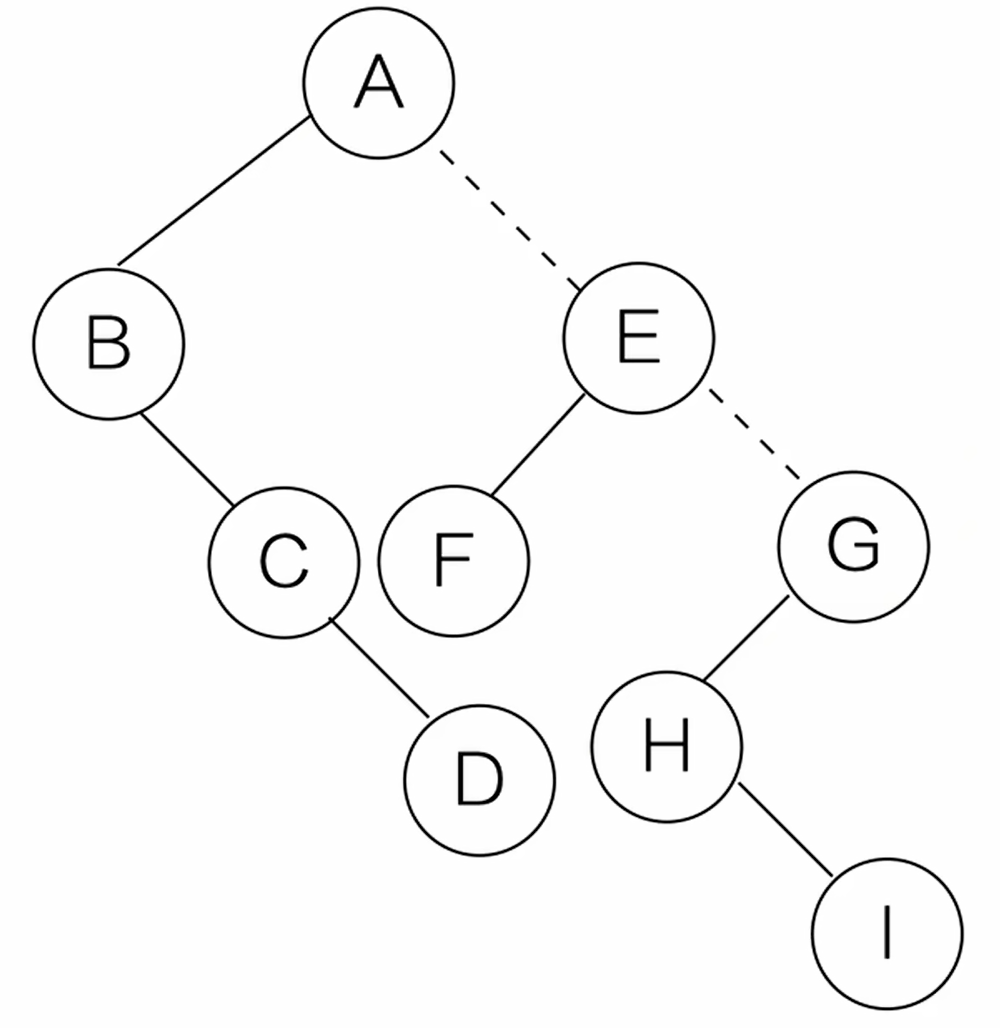
（2）拆开

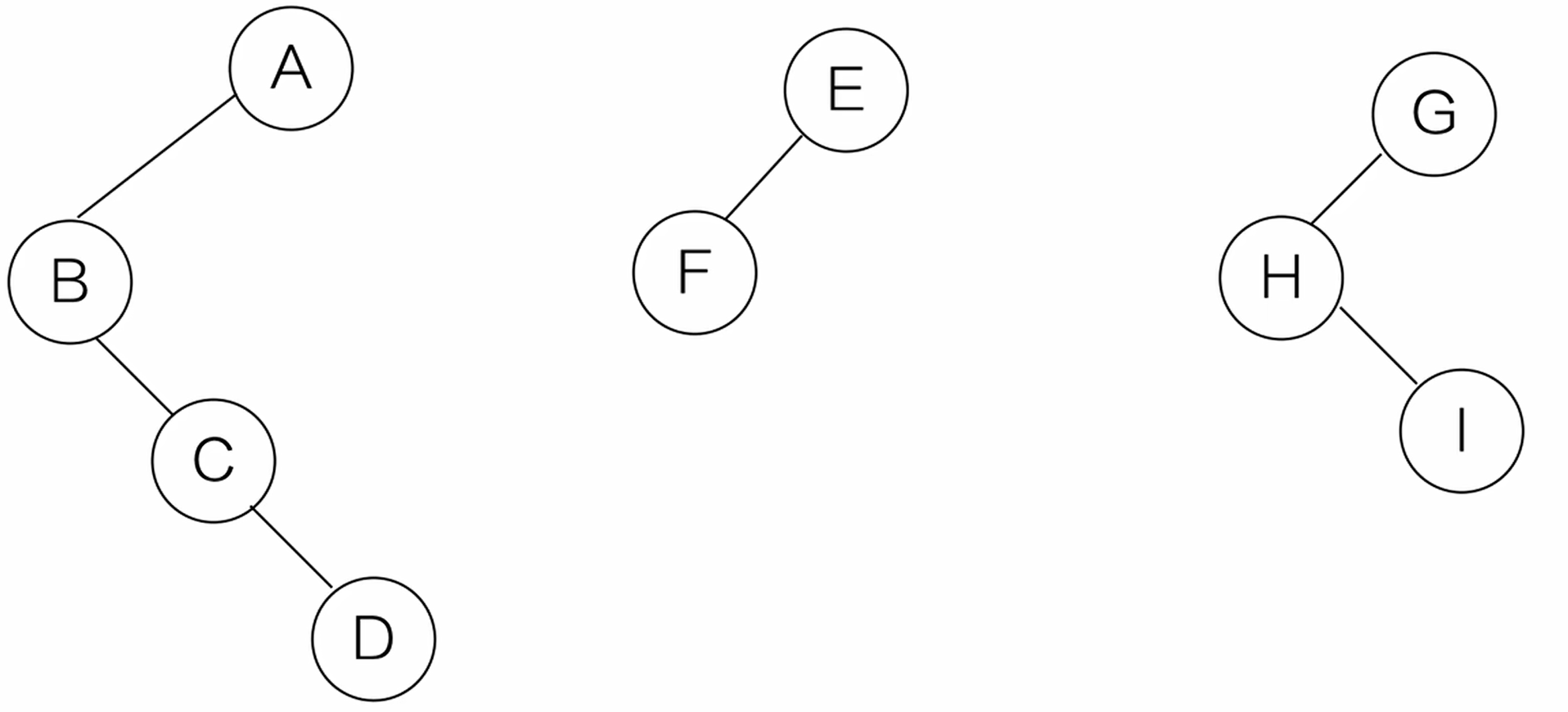
（3）再把每一个二叉树转换成树

三、图 搜索策略

1. 基本概念

图，是由顶点的有穷非空集合和顶点之间边的集合组成的。

通常记为G(V,E)，其中G表示图，V是G中顶点的集合，E是边的集合。

V(G)表示图顶点的集合；E()G表示图边的集合。

注意：对于图来说，不允许没有顶点，但边可以为空。

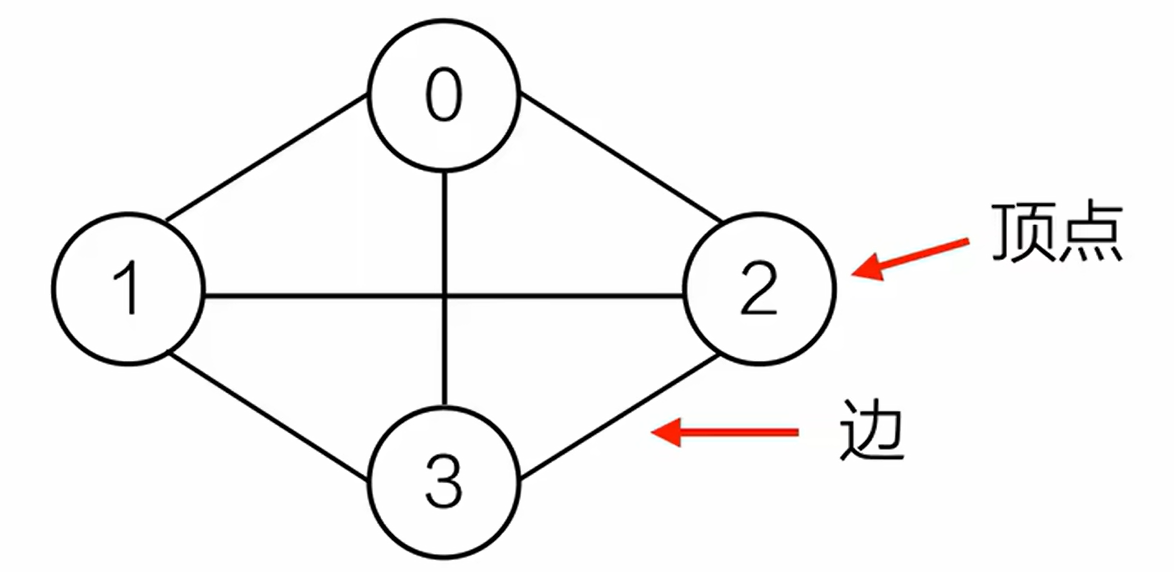
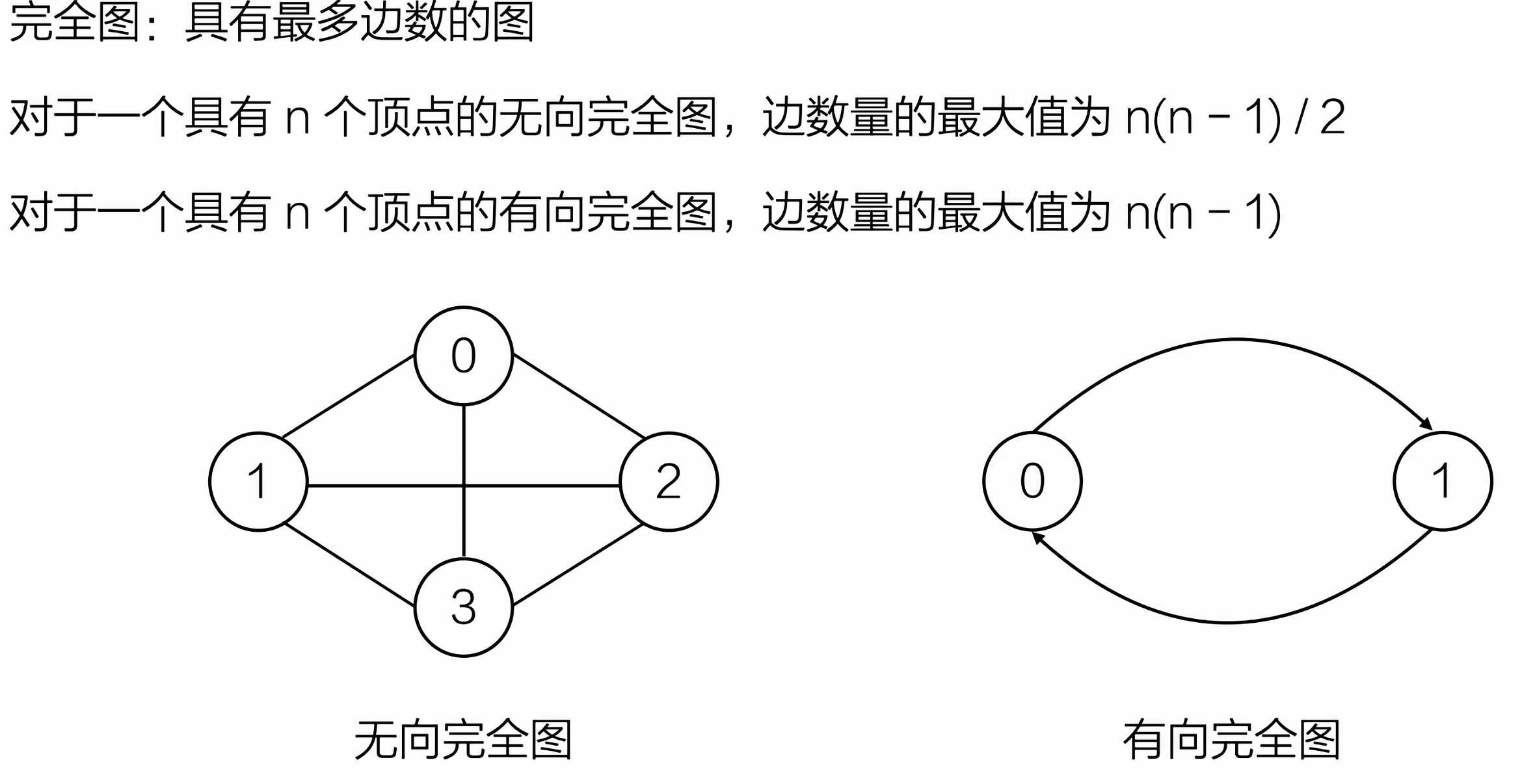
无向图和有向图

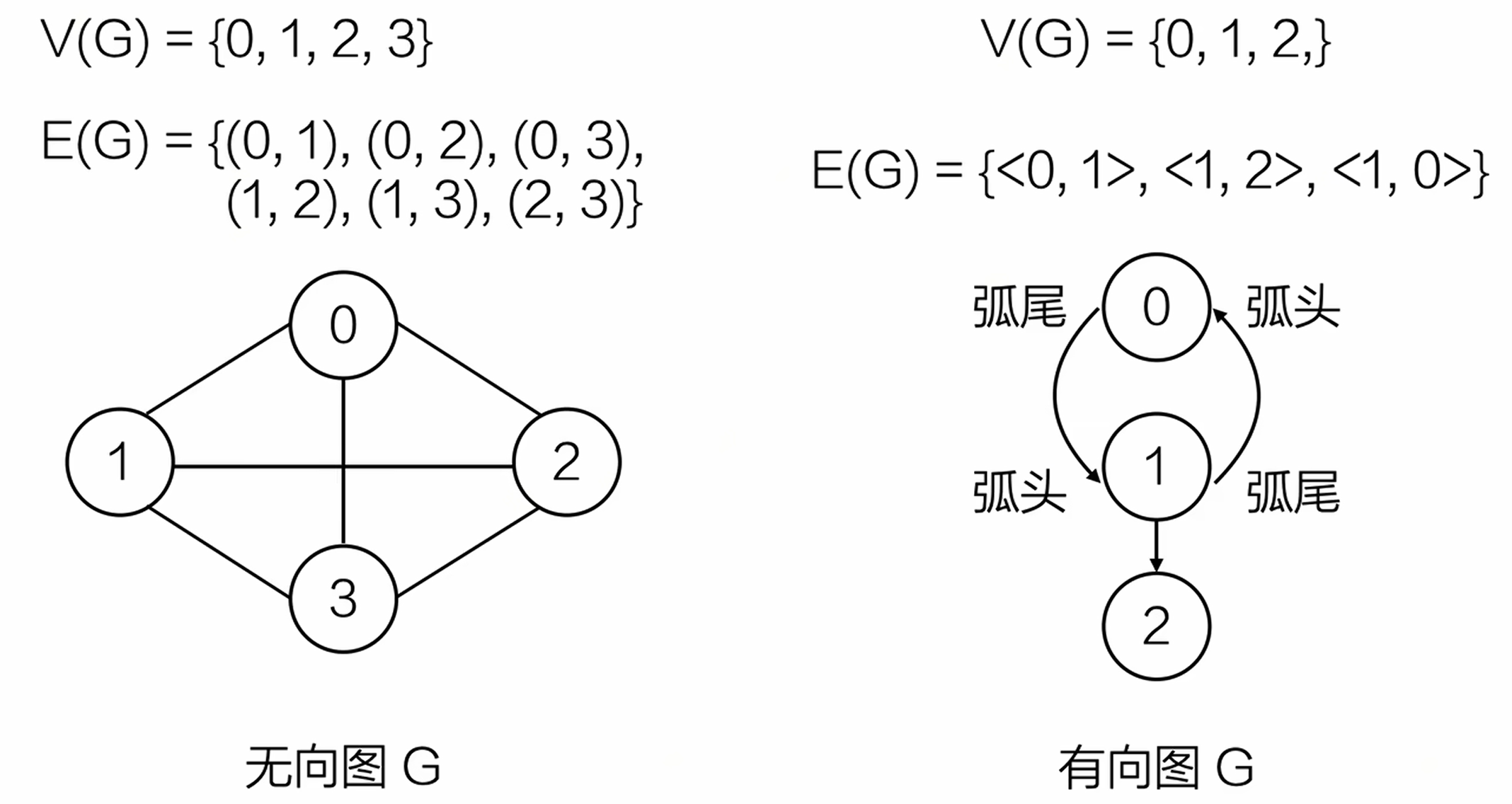
完全图

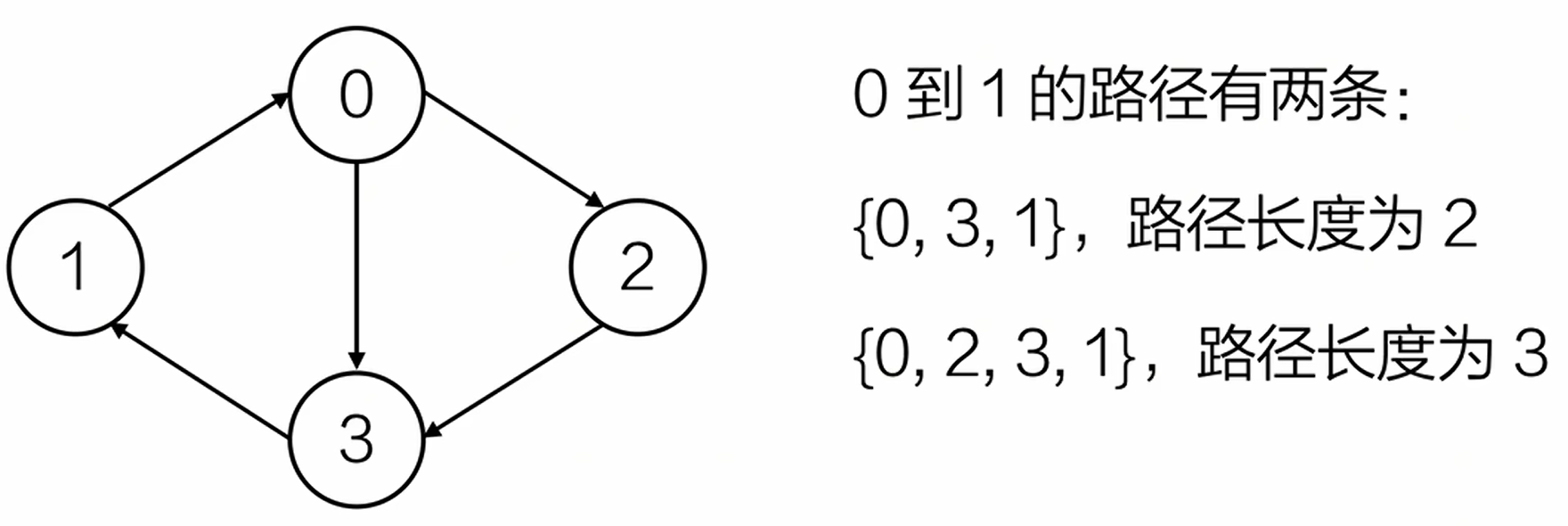
路径和路径长度

路径：从一个顶点开始，经过一系列的边到达另一个顶点形成的顶点序列。

路径长度：路径上边的数量。

回路(环)：起点和终点相同，路径{0,3,1,0}就是一个回路(环)。

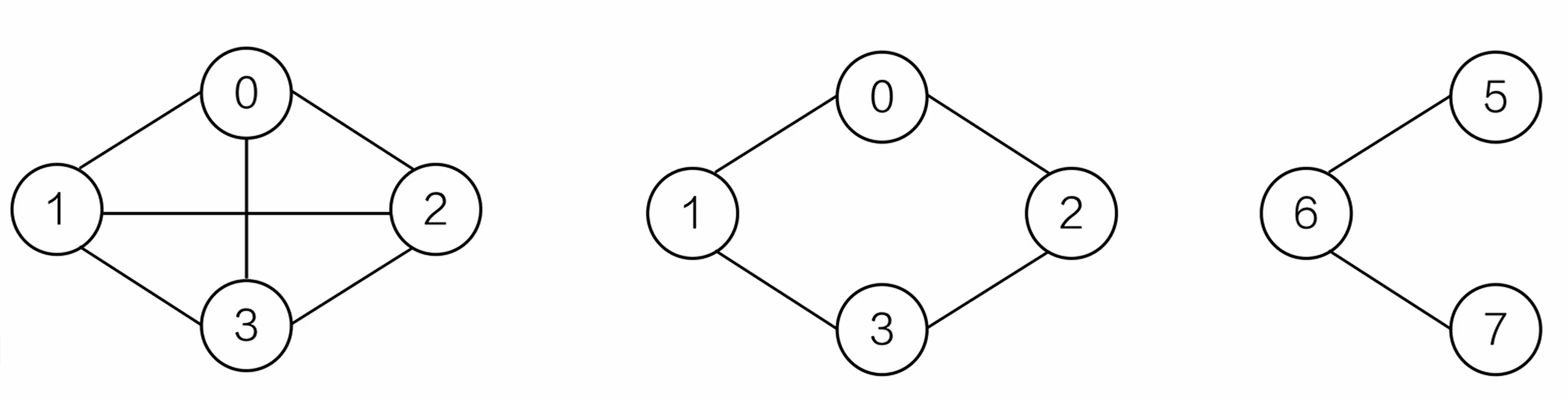
简单路径和简单回路

简单路径：路径中没有重复的顶点

简单回路：除第一个和最后一个顶点外，路径中没有重复的顶点

顶点的度

度：对于无向图来说，顶点的度就是指与顶点相关联边的数量。

出度：在有向图中，对于某个顶点，箭头指向该顶点边的数目。

入度：在有向图中，对于某个顶点，从该顶点出发边的数目。

连通图

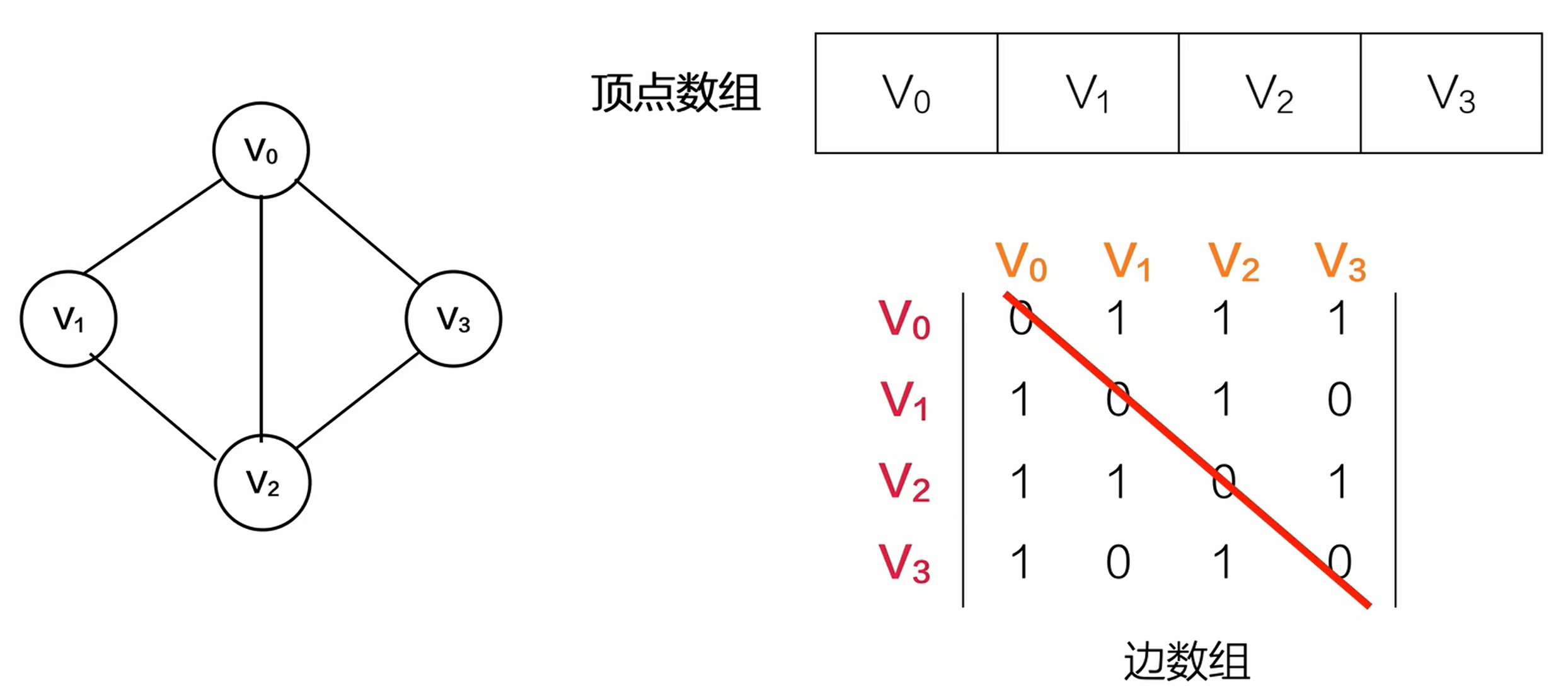
2. 图的存储

邻接矩阵 - 无向

邻接矩阵 - 无有

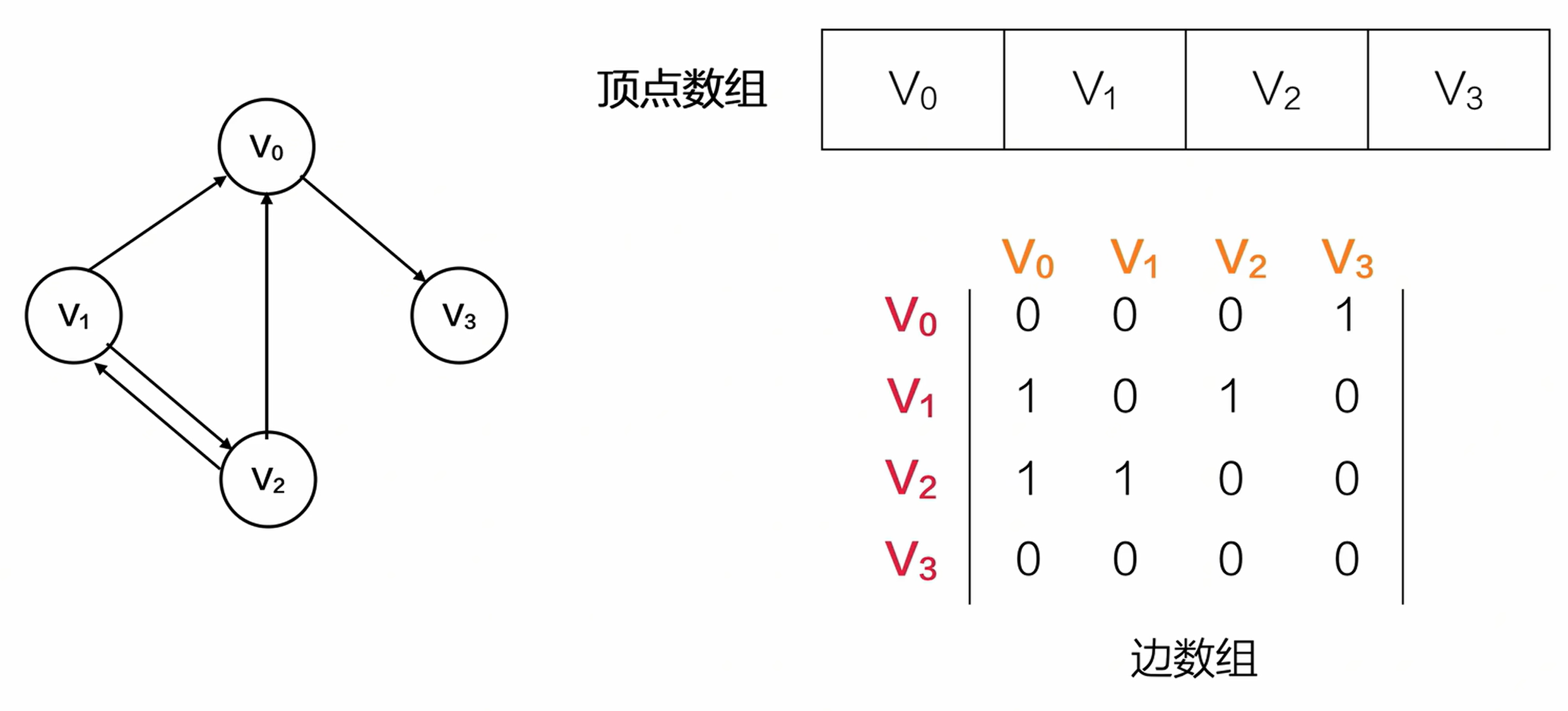
邻接矩阵 - 带权值

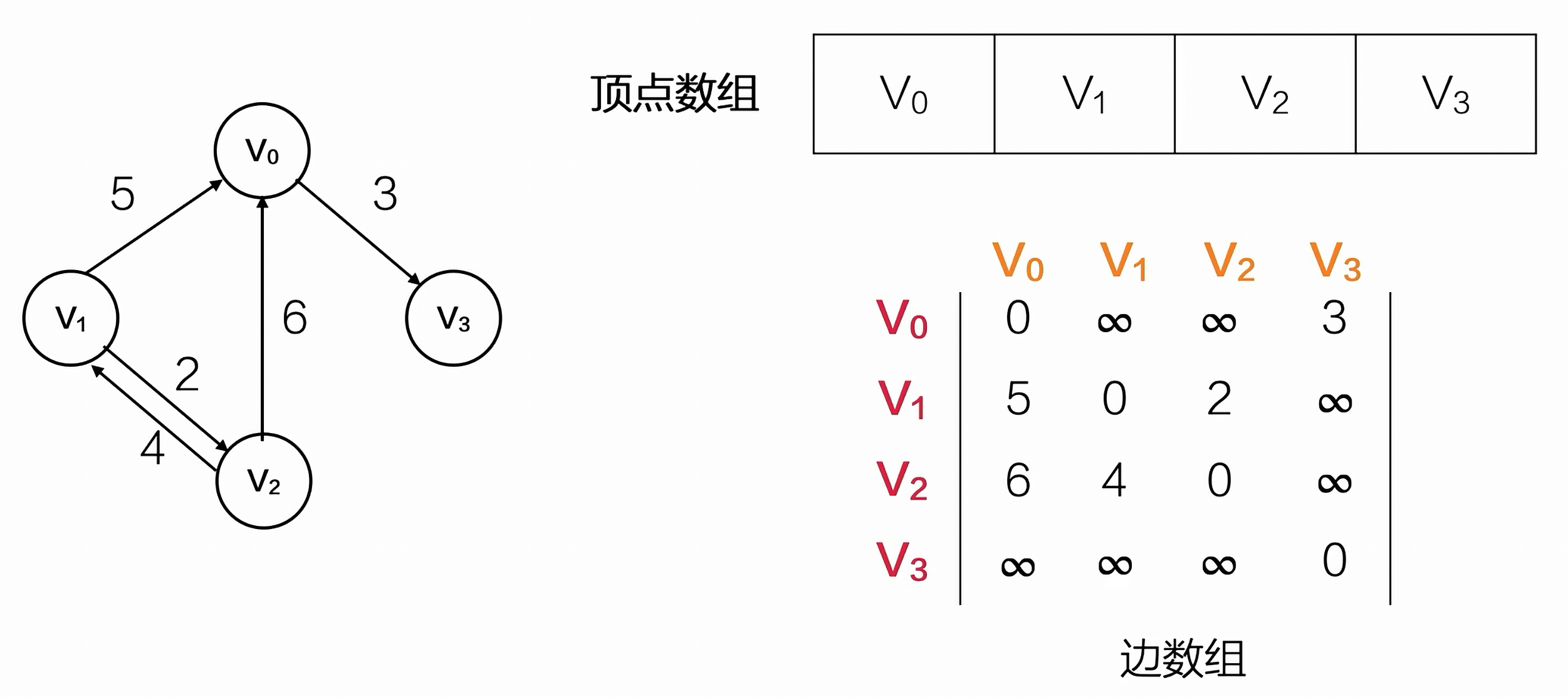
领接表 - 无向

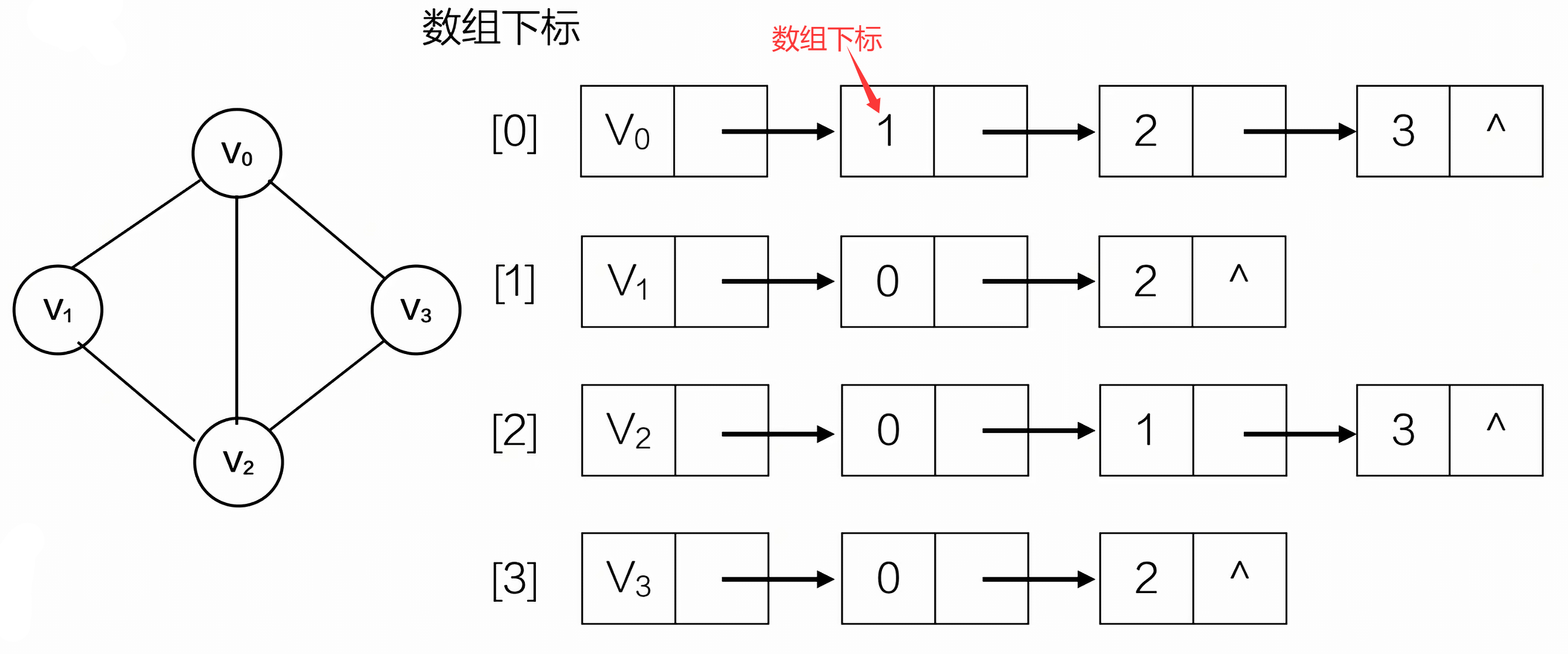
领接表 - 有向

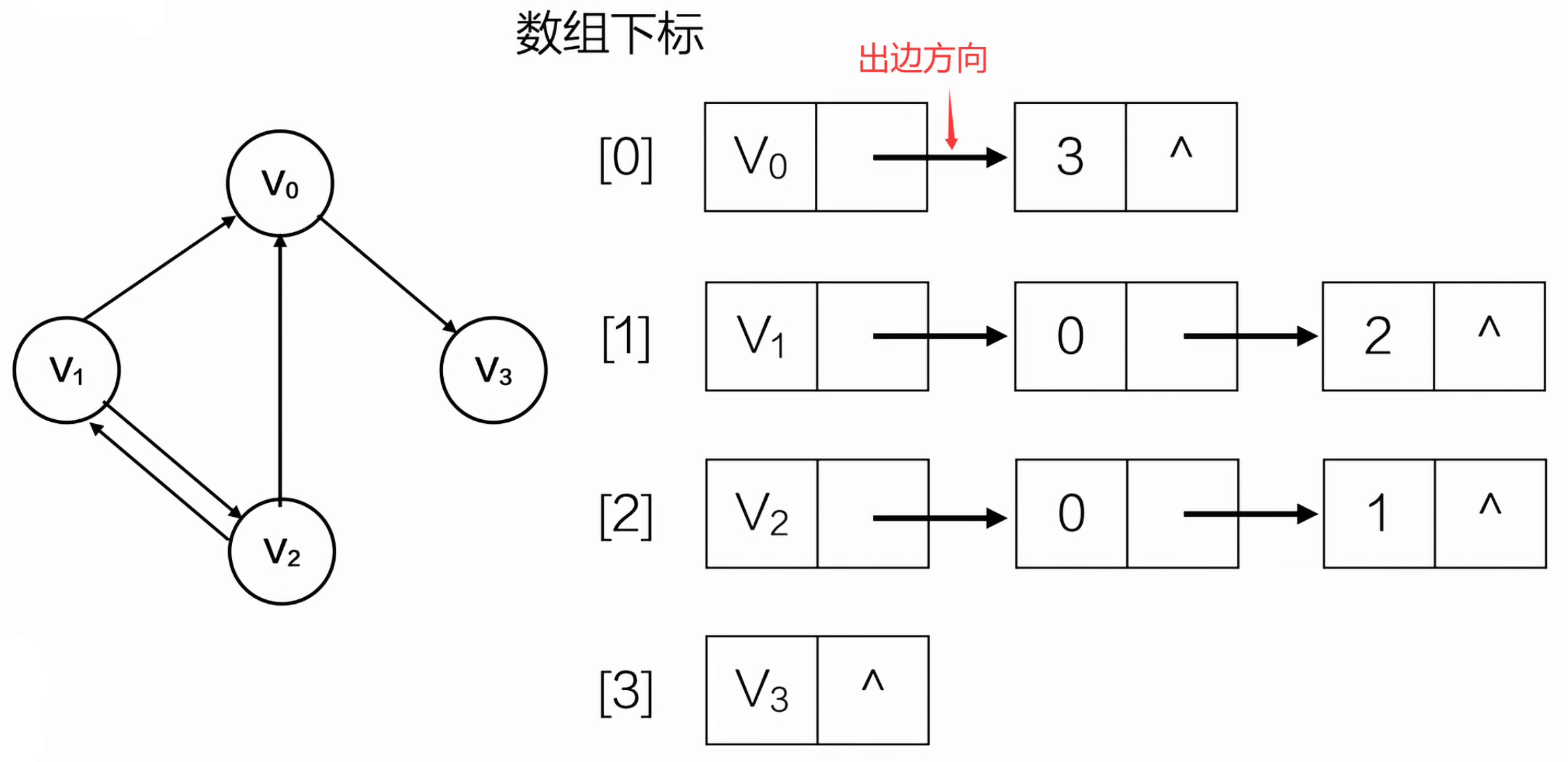
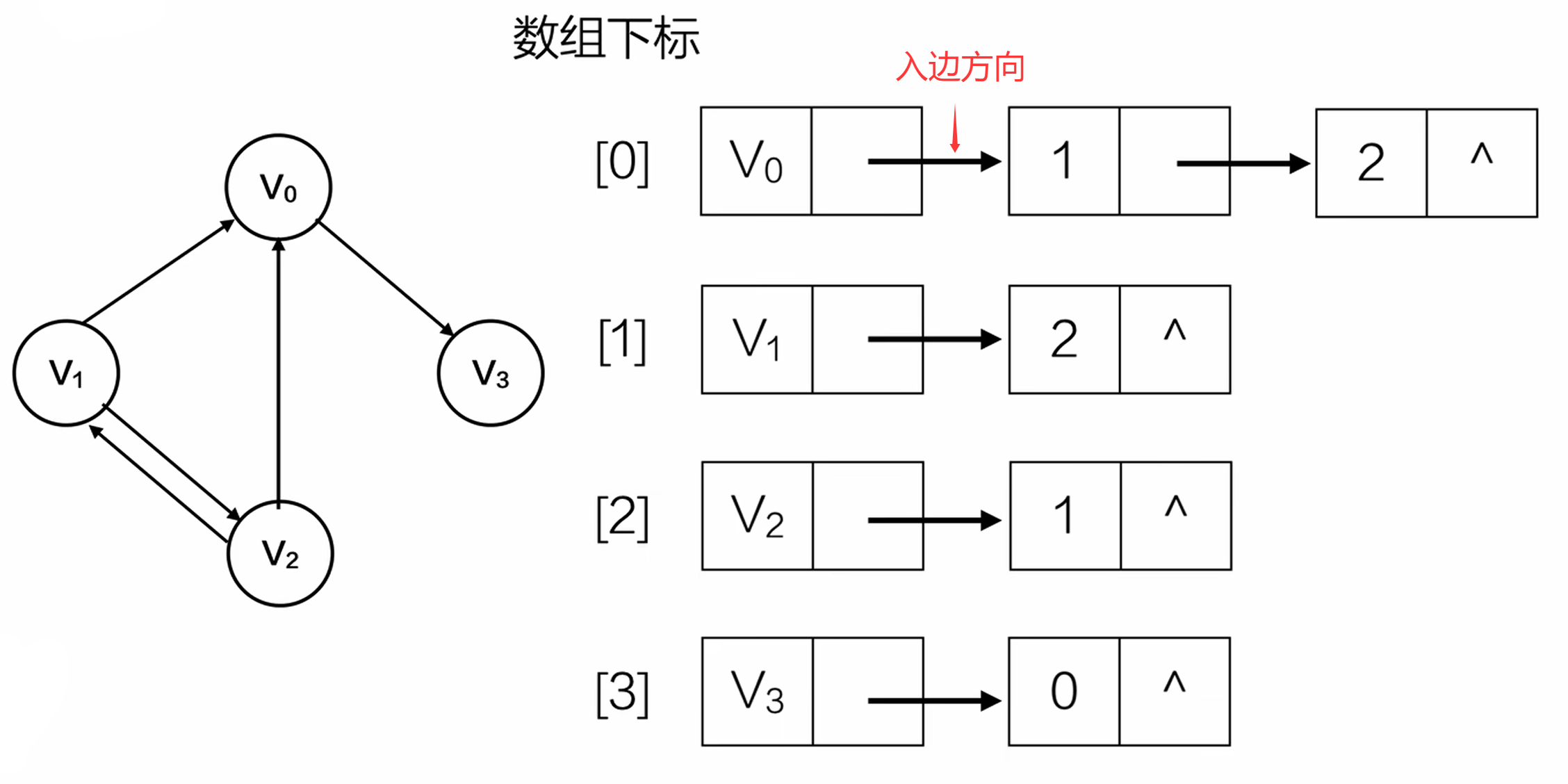
逆邻接表 - 有向（解决找寻入边问题）