队列：数据结构中的”排队艺术“

        今天我们介绍的是另一种特殊的线性表：队列。

一.队列的概念

        队列是一种只允许在一端进行插入数据操作，在另一端进行删除操作的特殊线性表，队列中的数据遵从FIFO(First In First Out)原则。

        入队列：进行插入数据的一端叫做队尾。

        出队列：进行删除操作的一段叫做队头。

二.队列的结构

图示：

        首先，我们需要决定队列的底层结构是数组还是链表：

        1.底层结构为数组

        以数组头部作为队头，数组尾部作为队尾

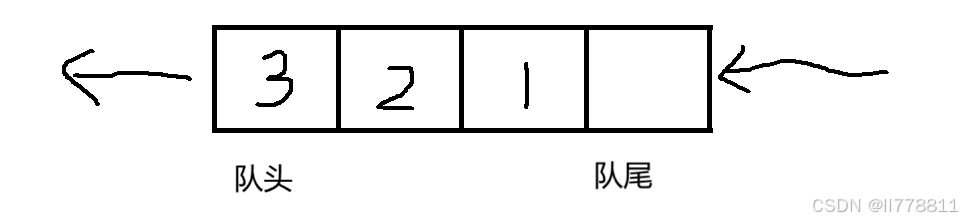
        则入队列时间复杂度为O(1)，出队列时间复杂度为O(n)。

        以数组头部作为队尾，数组尾部作为队头

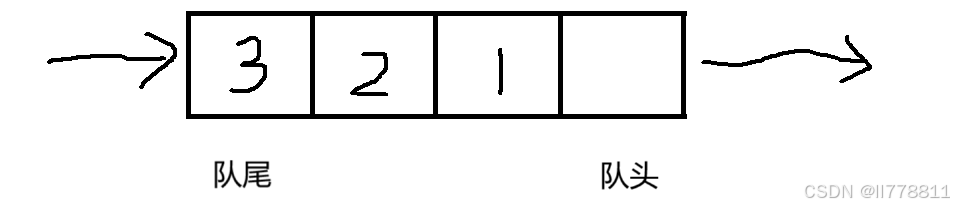
        则入队列时间复杂度为O(n)，出队列时间复杂度为O(1)。

        2.底层结构为链表

        以链表的头部为队头

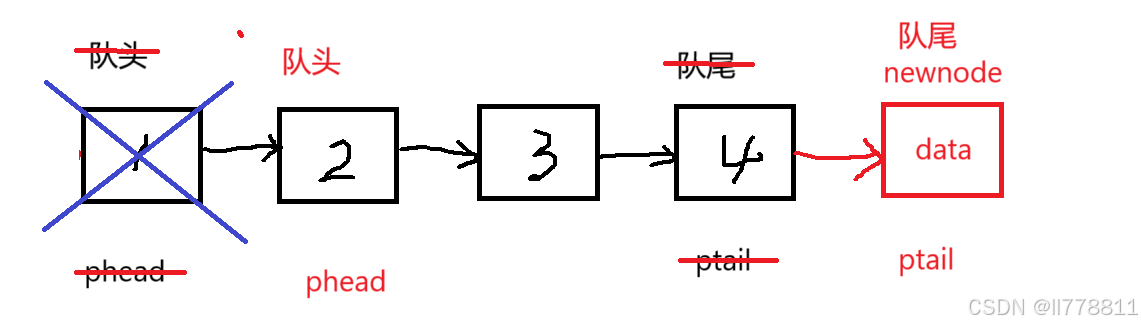
        则入队列时间复杂度为O(n)，出队列时间复杂度为O(1)。

        以链表的尾部为队头

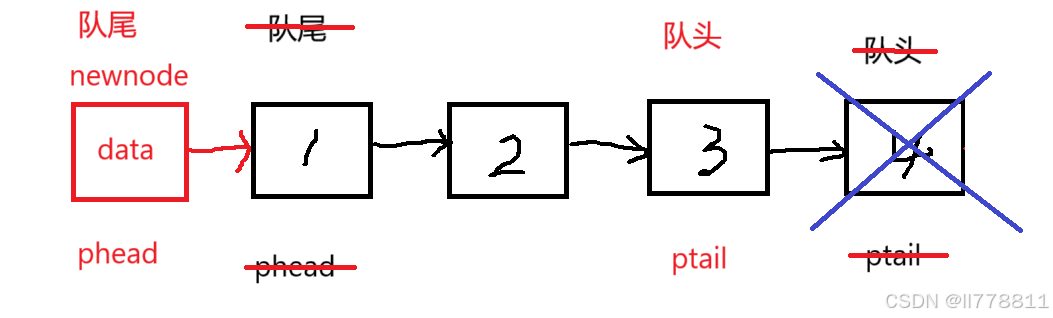        则入队列时间复杂度为O(1)，出队列时间复杂度为O(n)。

        综上：是否能有一种方法让入队列和出队列的时间复杂度均为O(1)?

        在这里我们定义两个结构体：

        第一个先定义队列的结点的结构

// 链式结构：表示队列 
typedef struct QListNode
{
	struct QListNode* _next;
	QDataType _data;
}QNode;

         QDataType为有效数据类型。

        第二个定义队列的结构

// 队列的结构 
typedef struct Queue
{
	QNode* _front;
	QNode* _rear;
	int size;
}Queue;

        _front为队头，_rear为队尾，size为队列中有效数据个数。

        这样的话以链表头部为队头，插入数据时无需通过遍历就可以直接找到队尾，使入队列与出队列操作时间复杂度均为O(1)。

三.队列的实现

1.初始化

void QueueInit(Queue* q)

        将队头与队尾置空，size赋值为0，即可实现初始化。

完整代码：

void QueueInit(Queue* q)
{
	assert(q);
	q->_front = q->_rear = NULL;
	q->size = 0;
}

2.入队列

void QueuePush(Queue* q, QDataType data)

        首先，动态申请一个新的队列结点。

QNode* newnode = (QNode*)malloc(sizeof(QNode));
if (newnode == NULL)
{
	perror("malloc");
	exit(1);
}
newnode->_data = data;
newnode->_next = NULL;

        当队列为空，即队头为NULL，使队头和队尾同时指向新结点。

if (q->_front == NULL)
{
	q->_front = q->_rear = newnode;
}

        当队列不为空，使队尾的next指针指向新结点，并将指向队尾的指针指向新结点。

else
{
	q->_rear->_next = newnode;
	q->_rear = q->_rear->_next;
}

        最后再将size加一。

++q->size;

完整代码：

// 队尾入队列 
void QueuePush(Queue* q, QDataType data)
{
	assert(q);
	QNode* newnode = (QNode*)malloc(sizeof(QNode));
	if (newnode == NULL)
	{
		perror("malloc");
		exit(1);
	}
	newnode->_data = data;
	newnode->_next = NULL;

	if (q->_front == NULL)
	{
		q->_front = q->_rear = newnode;
	}
	else
	{
		q->_rear->_next = newnode;
		q->_rear = q->_rear->_next;
	}
	++q->size;
}

3.出队列

void QueuePop(Queue* q)

        首先，需要对队列判空，这里单独封装一个函数来检测队列是否为空，当队头为NULL，则队列为空，返回非0，不为空则返回0。

int QueueEmpty(Queue* q)
{
	assert(q);
	return q->_front == NULL;
}

        判空后，若队列中只剩下一个数据，即队头和队尾指向同一个结点时，则直接将队头释放，并将队头和队尾置空。

if (q->_front == q->_rear)
{
	free(q->_front);
	q->_front = q->_rear = NULL;
}

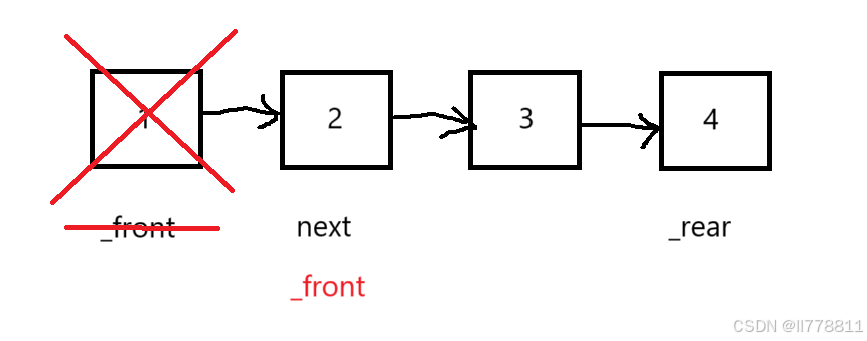
        若队列中元素大于一，保存队头的下一个结点，并将队头释放，再将队头指向保存的结点。

图示：

else
{
	QNode* next = q->_front->_next;
	free(q->_front);
	q->_front = next;
}

         最后再将size减一。

--q->size;

完整代码：

// 队头出队列 
void QueuePop(Queue* q)
{
	assert(!QueueEmpty(q));
	if (q->_front == q->_rear)
	{
		free(q->_front);
		q->_front = q->_rear = NULL;
	}
	else
	{
		QNode* next = q->_front->_next;
		free(q->_front);
		q->_front = next;
	}
	--q->size;
}

4.获取队列头部元素

QDataType QueueFront(Queue* q)

        首先对队列进行判空。

assert(!QueueEmpty(q));

        再返回队头存储数据即可。

完整代码：

QDataType QueueFront(Queue* q)
{
	assert(!QueueEmpty(q));
	return q->_front->_data;
}

5.获取队列队尾元素

        与获取队列头部元素方式相同，返回队列尾部元素即可。

QDataType QueueBack(Queue* q)
{
	assert(!QueueEmpty(q));
	return q->_rear->_data;
}

6.获取队列中有效元素个数

        直接返回size即可获取队列中有效元素个数。

int QueueSize(Queue* q)
{
	assert(q);
	return q->size;
}

7.销毁

        队列的销毁由于底层结构为链表，销毁方式与链表类似。

        从头部开始遍历，依次销毁每个节点，每次销毁时保存下个结点的地址。

QNode* pcur = q->_front;
while (pcur)
{
	QNode* next = pcur->_next;
	free(pcur);
	pcur = next;
}

        跳出循环后，将队头和队尾置空，size置为0。

q->_front = q->_rear = NULL;
q->size = 0;

完整代码：

void QueueDestroy(Queue* q)
{
	assert(q);
	QNode* pcur = q->_front;
	while (pcur)
	{
		QNode* next = pcur->_next;
		free(pcur);
		pcur = next;
	}
	q->_front = q->_rear = NULL;
	q->size = 0;
}

四.代码总览

void QueueInit(Queue* q)
{
	assert(q);
	q->_front = q->_rear = NULL;
	q->size = 0;
}

// 队尾入队列 
void QueuePush(Queue* q, QDataType data)
{
	assert(q);
	QNode* newnode = (QNode*)malloc(sizeof(QNode));
	if (newnode == NULL)
	{
		perror("malloc");
		exit(1);
	}
	newnode->_data = data;
	newnode->_next = NULL;

	if (q->_front == NULL)
	{
		q->_front = q->_rear = newnode;
	}
	else
	{
		q->_rear->_next = newnode;
		q->_rear = q->_rear->_next;
	}
	++q->size;
}

// 检测队列是否为空，如果为空返回非零结果，如果非空返回0 
int QueueEmpty(Queue* q)
{
	assert(q);
	return q->_front == NULL;
}

// 队头出队列 
void QueuePop(Queue* q)
{
	assert(!QueueEmpty(q));
	if (q->_front == q->_rear)
	{
		free(q->_front);
		q->_front = q->_rear = NULL;
	}
	else
	{
		QNode* next = q->_front->_next;
		free(q->_front);
		q->_front = next;
	}
	--q->size;
}

// 获取队列头部元素 
QDataType QueueFront(Queue* q)
{
	assert(!QueueEmpty(q));
	return q->_front->_data;
}

// 获取队列队尾元素 
QDataType QueueBack(Queue* q)
{
	assert(!QueueEmpty(q));
	return q->_rear->_data;
}

// 获取队列中有效元素个数 
int QueueSize(Queue* q)
{
	assert(q);
	return q->size;
}

// 销毁队列 
void QueueDestroy(Queue* q)
{
	assert(q);
	QNode* pcur = q->_front;
	while (pcur)
	{
		QNode* next = pcur->_next;
		free(pcur);
		pcur = next;
	}
	q->_front = q->_rear = NULL;
	q->size = 0;
}

五.总结

        队列的定义比较特殊，需要单独定义队头和队尾，但可以借助前面链表的内容进行学习，下一期我们将进入二叉树的世界中，并实现顺序二叉树：堆。