栈：数据结构中的“时间管理大师”

最新推荐文章于 2025-12-05 14:45:56 发布

原创最新推荐文章于 2025-12-05 14:45:56 发布 · 877 阅读

7 ·

CC 4.0 BY-SA版权

文章标签：

#数据结构 #c语言 #开发语言

继链表与顺序表的完结后，接下来要介绍的是另外两个线性表：栈与队列，本期我们先介绍的是栈的实现。

一.栈的概念

栈是一种特殊的线性表，其在逻辑结构上连续，在物理结构上不一定连续，其物理结构的连续性取决于栈的底层实现逻辑是数组还是链表。

栈只能在固定的一端进行插入和删除操作，这一端被称为栈顶，另一端称为栈底。栈中的语速遵循LIFO(Last In First Out)原则。

压栈：栈的插入数据操作叫做压栈，在栈顶入数据。

出栈：栈的删除数据操作叫做出栈，也在栈顶出数据。

二.栈的结构

图示：

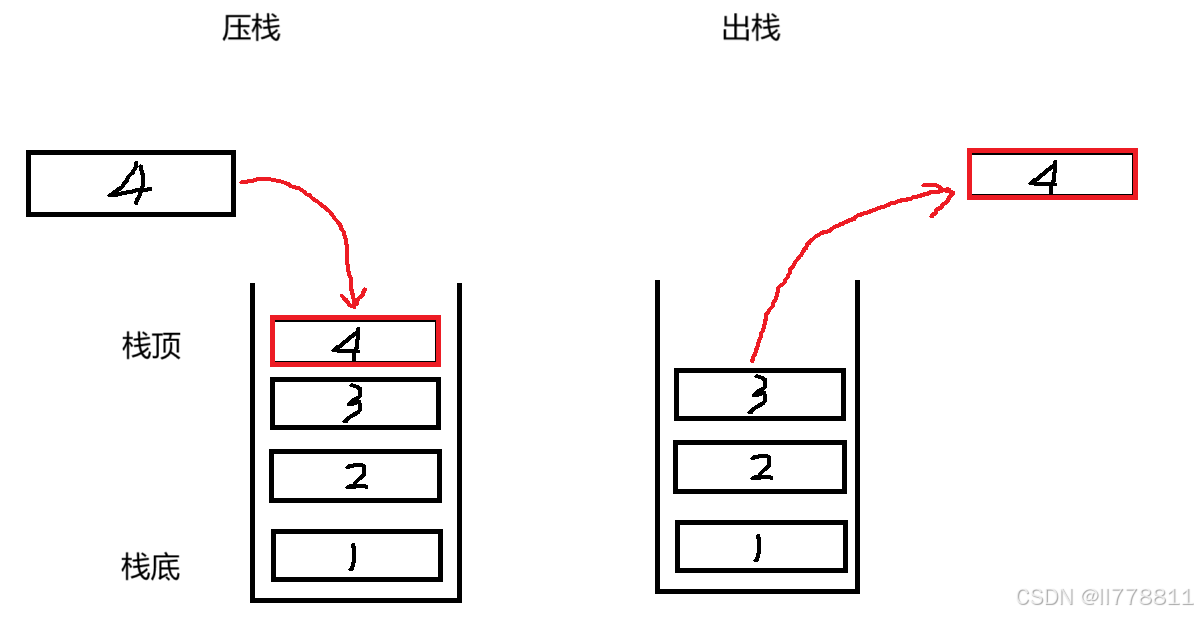
首先先来决定栈的底层结构：

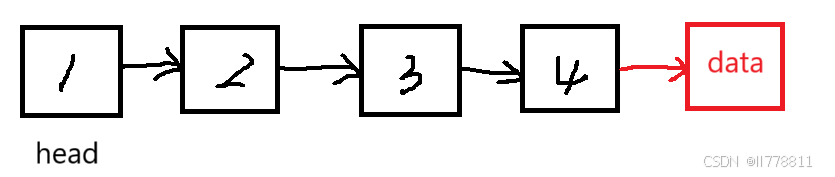
1.顶层结构为链表

将链表的尾部当作栈顶，那么每次插入和删除数据都需要遍历，时间复杂度都为O(n)。

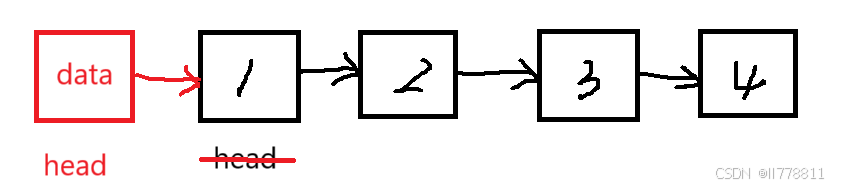
将链表的头部当作栈顶，那么每次插入和删除数据都需要改变头结点的指向。

2.底层结构为数组

将数组的头部作为栈顶，那么入栈出栈时间复杂度均为O(1)。

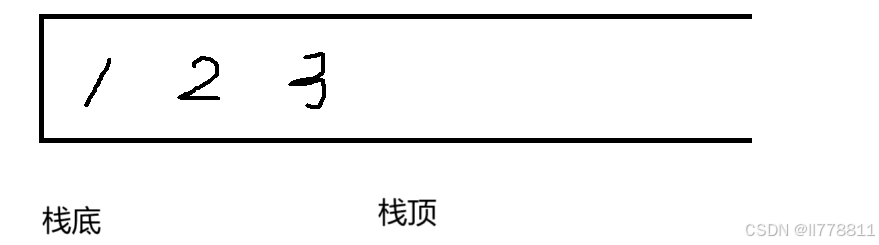
所以我们这里将数组作为栈的底层结构。

typedef int STDataType;
typedef struct Stack
{
	STDataType* _a;
	int _top;		// 栈顶
	int _capacity;  // 容量 
}Stack;

图示：

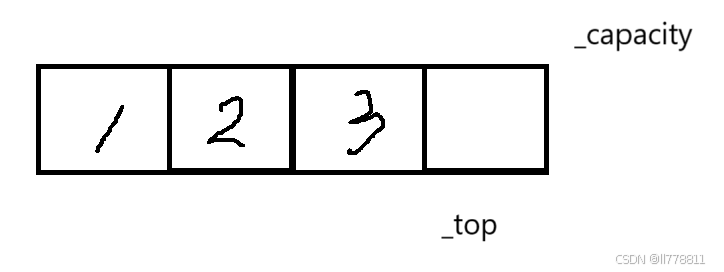
这里我们定义一个可以动态申请数组空间的指针，_top指向栈顶元素的下一个位置，_capacity为数组当前容量，到这里就是通过代码实现栈的结构。

三.栈的实现

1.初始化

void StackInit(Stack* ps)

将指针置为空，栈顶和容量置为0即可实现初始化。

完整代码：

void StackInit(Stack* ps)
{
	ps->_a = NULL;
	ps->_top = ps->_capacity = 0;
}

2.入栈

void StackPush(Stack* ps, STDataType data)

首先，由于栈的底层逻辑是数组，与之前所讲的顺序表类似，入栈前我们需要判断栈中空间是否足够，用_top和_capacity进行比较，若空间不够则进行扩容操作，并将capacity设置为新容量。

if (ps->_top == ps->_capacity)
{
	int newcapacity = ps->_capacity == 0 ? 4 : 2 * ps->_capacity;
	STDataType* tmp = (STDataType*)realloc(ps->_a, newcapacity * sizeof(STDataType));
	if (tmp == NULL)
	{
		perror("realloc");
		exit(1);
	}
	ps->_a = tmp;
	ps->_capacity = newcapacity;
}

· 如果空间足够，那么直接将元素放在栈顶位置，之后让栈顶自增一。

ps->_a[ps->_top++] = data;

完整代码：

// 入栈 
void StackPush(Stack* ps, STDataType data)
{
	assert(ps);
	if (ps->_top == ps->_capacity)
	{
		int newcapacity = ps->_capacity == 0 ? 4 : 2 * ps->_capacity;
		STDataType* tmp = (STDataType*)realloc(ps->_a, newcapacity * sizeof(STDataType));
		if (tmp == NULL)
		{
			perror("realloc");
			exit(1);
		}
		ps->_a = tmp;
		ps->_capacity = newcapacity;
	}
	ps->_a[ps->_top++] = data;
}

3.出栈

在出栈前，我们需要对栈进行判空操作，若栈顶与栈底相等均为0，则栈为空，这里单独封装一个函数判空，若为空返回非0值，若不为空返回0。

int StackEmpty(Stack* ps)
{
	assert(ps);
	return ps->_top == 0;
}

在判空操作后，与顺序表类似，只需让栈顶减一即可实现出栈操作。

完整代码：

void StackPop(Stack* ps) 
{
	assert(!StackEmpty(ps));
	--ps->_top;
}

4.获取栈顶元素

STDataType StackTop(Stack* ps)

先进行判空。

assert(!StackEmpty(ps));

图示：

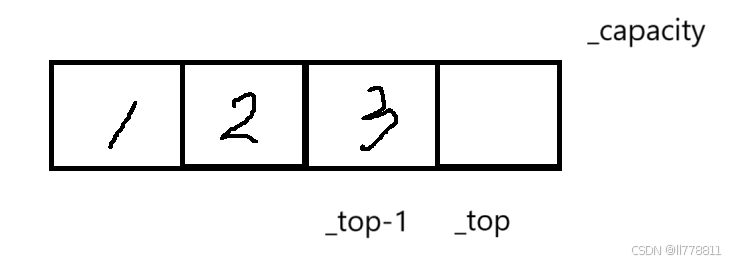
返回_top-1下标的元素即可。

完整代码：

STDataType StackTop(Stack* ps)
{
	assert(!StackEmpty(ps));
	return ps->_a[ps->_top - 1];
}

5.获取栈中有效元素个数

int StackSize(Stack* ps)

由于_top位置为栈顶元素下标加一，返回_top即可。

int StackSize(Stack* ps)
{
	assert(ps);
	return ps->_top;
}

6.销毁

与顺序表的销毁相同，先销毁动态申请的数组，再将栈顶和容量置为0.

完整代码：

void StackDestroy(Stack* ps)
{
	if (ps->_a)
		ps->_a = NULL;
	ps->_top = ps->_capacity = 0;
}

四.代码总览

// 初始化栈 
void StackInit(Stack* ps)
{
	ps->_a = NULL;
	ps->_top = ps->_capacity = 0;
}

// 入栈 
void StackPush(Stack* ps, STDataType data)
{
	assert(ps);
	if (ps->_top == ps->_capacity)
	{
		int newcapacity = ps->_capacity == 0 ? 4 : 2 * ps->_capacity;
		STDataType* tmp = (STDataType*)realloc(ps->_a, newcapacity * sizeof(STDataType));
		if (tmp == NULL)
		{
			perror("realloc");
			exit(1);
		}
		ps->_a = tmp;
		ps->_capacity = newcapacity;
	}
	ps->_a[ps->_top++] = data;
}

// 检测栈是否为空，如果为空返回非零结果，如果不为空返回0 
int StackEmpty(Stack* ps)
{
	assert(ps);
	return ps->_top == 0;
}

// 出栈 
void StackPop(Stack* ps) 
{
	assert(!StackEmpty(ps));
	--ps->_top;
}

// 获取栈顶元素 
STDataType StackTop(Stack* ps)
{
	assert(!StackEmpty(ps));
	return ps->_a[ps->_top - 1];
}

// 获取栈中有效元素个数 
int StackSize(Stack* ps)
{
	assert(ps);
	return ps->_top;
}

// 销毁栈 
void StackDestroy(Stack* ps)
{
	if (ps->_a)
		ps->_a = NULL;
	ps->_top = ps->_capacity = 0;
}