顺序表：数据结构的基石

于 2025-01-11 23:08:35 发布
阅读量833 收藏 15
点赞数 31
CC 4.0 BY-SA版权
文章标签： c语言 开发语言 数据结构
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/ll778811/article/details/145079130

目录

一.线性表的基本概念

二.顺序表

1.顺序表的基本概念

2.顺序表的分类

2.1静态顺序表

2.2动态顺序表

3.动态顺序表的实现

3.1顺序表的建立

3.2顺序表的初始化

3.3尾插

3.4头插

3.5尾删

3.6头删

3.7查找

3.8在指定位置前插入数据

3.9在指定位置删除数据

3.10顺序表销毁

三.代码总览

四.总结

 今天我们要介绍的是数据结构中的顺序表 ，在介绍顺序表之前，我们首先要了解线性表的概念。

一.线性表的基本概念

        线性表是一种常见的数据结构，它是由n个相同类型的元素所构成的有限序列，它在逻辑结构上呈现连续的形态，但在物理结构上不一定连续，如链表等。

二.顺序表

1.顺序表的基本概念

        顺序表是属于线性表的一种，它在逻辑与物理结构上都是连续的，它是用一段物理地址连续的储存单元去储存数据元素的数据结构，常常通过数组去进行实现，与数组不同的是，顺序表增加了增删改查等接口。

2.顺序表的分类
2.1静态顺序表

        静态顺序表示用定长数组去储存数据元素，虽然不用调整内存空间的大小，但是也容易出现内存空间开辟不足和浪费空间的问题，所以我们这里主要讨论的是动态顺序表。

2.2动态顺序表

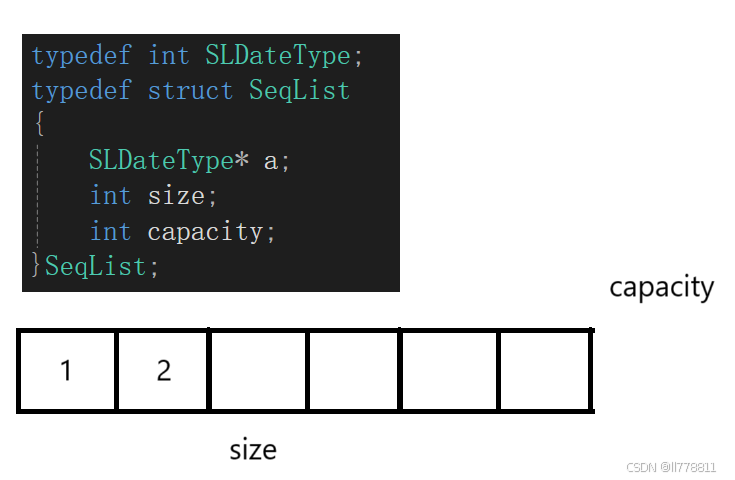
       图中的size表示当前顺序表中所储存的有效数据个数，而capacity表示的是当前顺序表中的数据空间容量。所储存的数据个数大于容量时，我们可以通过动态内存分配去进行扩容的操作，这是与静态顺序表不同的地方。

3.动态顺序表的实现
3.1顺序表的建立
typedef int SLDataType;
typedef struct SeqList
{
	SLDataType* a;
	int size;
	int capacity;
}SeqList;

        这里将int重命名为SLDataType可以在顺序表存储其他类型的数据时方便修改。

3.2顺序表的初始化
void SeqListInit(SeqList* ps)
{
	ps->a = NULL;
	ps->size = 0;
	ps->capacity = 0;
}

        在初始化中，不仅要将size和capacity置为0，也要将a这个指向数组的指针置为空指针，避免出现野指针，同时SeqListInit的参数也要接收结构体指针，实现传址调用。

3.3尾插

        在插入前应检查空间是否足够，在这里封装一个扩展空间的函数SLCheckCapacity

void SLCheckCapacity(SeqList* ps)
{
	if (ps->size == ps->capacity)
	{
		//扩容
		int newcapacity = ps->capacity == 0 ? 4 : 2 * ps->capacity;
		SLDateType* tmp = (SLDateType*)realloc(ps->a, newcapacity * sizeof(SLDateType));
		if (tmp == NULL)
		{
			perror("realloc");
			exit(1);
		}
		ps->a = tmp;
		ps->capacity = newcapacity;
	}
}

        通过判断size与capacity的大小关系，执行扩容操作。如果是，这里将扩容的空间大小设置为原空间的两倍，不会过度浪费空间，若原空间大小为0时，默认扩容4个数据空间，并将capacity设置为对应的数据空间个数。

void SeqListPushBack(SeqList* ps, SLDataType x)
{
	//检查空间是否足够
	SLCheckCapacity(ps);
	ps->a[ps->size++] = x;
}

         在扩容操作之后，插入对应的数据，并将有效数据个数自增一。

3.4头插

         与尾插不同的是，头插之前，先要判断顺序表是否为空，这里使用断言进行判断

void SeqListPushFront(SeqList* ps, SLDataType x)
{
	assert(ps);
	SLCheckCapacity(ps);
	for (int i = ps->size; i > 0; i--)
	{
		ps->a[i] = ps->a[i - 1];
	}
	ps->a[0] = x;
	++ps->size;
}

         我们首先判断是否需要扩容，再将顺序表中的数据后移一位，将插入的数据放在数组首位，从而实现头插，最后让有效数据个数自增一。

        时间复杂度为O(n)

3.5尾删
void SeqListPopBack(SeqList* ps)
{
	//顺序表不能为空
	assert(ps && ps->size);

	--ps->size;
}

         尾删要保证顺序表不为空，有效数据个数也不为0，这里将ps和size断言，并将有效数据个数减一，被删除的数据在物理结构中还是存在的，但在后续进行其他操作时，不会影响其他数据的变化。

3.6头删

        与尾删相同，顺序表与有效数据个数需要断言。

void SeqListPopFront(SeqList* ps)
{
	//顺序表不能为空
	assert(ps && ps->size);
	for (int i = 0; i < ps->size; i++)
	{
		ps->a[i] = ps->a[i + 1];
	}
	--ps->size;
}

        与尾删不同的是，需要将删除位置后的所有有效数据前移一位，最后让有效数据个数减一。

        时间复杂度为O(n)

3.7查找
int SeqListFind(SeqList* ps, SLDataType x)
{
	for (int i = 0; i < ps->size; i++)
	{
		if (ps->a[i] == x)
		{
			return i;
		}
	}
	return -1;
}

        顺序表的查找与数组的遍历查找类似，找到则返回相应数据的下标位置，没找到则返回-1。

        时间复杂度为O(n)       

3.8在指定位置前插入数据
void SeqListInsert(SeqList* ps, int pos, SLDataType x)
{
	assert(ps);
	assert(pos >= 0 && pos <= ps->size);
	SLCheckCapacity(ps);
	for (int i = ps->size; i > pos; i--)
	{
		ps->a[i] = ps->a[i - 1];
	}
	ps->a[pos] = x;
	++ps->size;
}

        pos为指定位置的下标，pos的范围在0~size，所以用断言来保证顺序表不为空，pos的值不超过有效范围，与头插不同的是，需要将预插入位置后的所有有效数据后移一位，再插入数据，有效数据个数自增一。

        时间复杂度为O(n)

3.9在指定位置删除数据
void SeqListErase(SeqList* ps, int pos)
{
	assert(ps);
	assert(pos >= 0 && pos < ps->size);

	for (int i = pos; i < ps->size - 1; i++)
	{
		ps->a[i] = ps->a[i + 1];
	}

	--ps->size;
}

        与在指定位置前插入数据的断言方式相同，保证指向顺序表的指针与pos为正常输入，之后将预删除位置后的所有有效数据前移一位，再让有效数据个数自减一。

        时间复杂度为O(n)

3.10顺序表销毁
void SeqListDestroy(SeqList* ps)
{
	//顺序表不能为空
	assert(ps);

	free(ps->a);
	ps->a = NULL;
	ps->size = 0;
	ps->capacity = 0;
}

        由于指向顺序表的指针是通过SLCheckCapacity中的realloc操作所开辟的内存空间，如果在程序结束后不及时释放。可能会造成内存泄漏等问题，所以我们这里将指针a释放，并置为空指针，再将有效数据个数与数据容量置为0，实现顺序表的销毁。

三.代码总览

//SeqList.h
#pragma once
#include <stdio.h>
#include <assert.h>
#include <stdlib.h>

typedef int SLDateType;
typedef struct SeqList
{
	SLDateType* a;
	int size;
	int capacity;
}SeqList;

//对数据的管理:增删查改 
void SeqListInit(SeqList* ps);
void SeqListDestroy(SeqList* ps);

void SeqListPrint(SeqList* ps);

void SeqListPushBack(SeqList* ps, SLDateType x);
void SeqListPushFront(SeqList* ps, SLDateType x);
void SeqListPopFront(SeqList* ps);
void SeqListPopBack(SeqList* ps);

// 顺序表查找
int SeqListFind(SeqList* ps, SLDateType x);
// 顺序表在pos位置插入x
void SeqListInsert(SeqList* ps, int pos, SLDateType x);
// 顺序表删除pos位置的值
void SeqListErase(SeqList* ps, int pos);
//SeqList.c
#include"SeqList.h"
//顺序表初始化
void SeqListInit(SeqList* ps)
{
	ps->a = NULL;
	ps->size = 0;
	ps->capacity = 0;
}

//顺序表销毁
void SeqListDestroy(SeqList* ps)
{
	//顺序表不能为空
	assert(ps);

	free(ps->a);
	ps->a = NULL;
	ps->size = 0;
	ps->capacity = 0;
}

void SLCheckCapacity(SeqList* ps)
{
	if (ps->size == ps->capacity)
	{
		//扩容
		int newcapacity = ps->capacity == 0 ? 4 : 2 * ps->capacity;
		SLDateType* tmp = (SLDateType*)realloc(ps->a, newcapacity * sizeof(SLDateType));
		if (tmp == NULL)
		{
			perror("realloc");
			exit(1);
		}
		ps->a = tmp;
		ps->capacity = newcapacity;
	}
}

//尾插
void SeqListPushBack(SeqList* ps, SLDateType x)
{
	//检查空间是否足够
	SLCheckCapacity(ps);
	ps->a[ps->size++] = x;
}

//头插
void SeqListPushFront(SeqList* ps, SLDateType x)
{
	assert(ps);
	SLCheckCapacity(ps);
	for (int i = ps->size; i > 0; i--)
	{
		ps->a[i] = ps->a[i - 1];
	}
	ps->a[0] = x;
	++ps->size;
}

//尾删
void SeqListPopBack(SeqList* ps)
{
	//顺序表不能为空
	assert(ps && ps->size);

	--ps->size;
}

//头删
void SeqListPopFront(SeqList* ps)
{
	//顺序表不能为空
	assert(ps && ps->size);
	for (int i = 0; i < ps->size; i++)
	{
		ps->a[i] = ps->a[i + 1];
	}
	--ps->size;
}

//顺序表查找
int SeqListFind(SeqList* ps, SLDateType x)
{
	for (int i = 0; i < ps->size; i++)
	{
		if (ps->a[i] == x)
		{
			return i;
		}
	}
	return -1;
}

//在指定位置前插入数据
void SeqListInsert(SeqList* ps, int pos, SLDateType x)
{
	assert(ps);
	assert(pos >= 0 && pos <= ps->size);

	SLCheckCapacity(ps);
	for (int i = ps->size; i > pos; i--)
	{
		ps->a[i] = ps->a[i - 1];
	}
	ps->a[pos] = x;
	++ps->size;
}

//在指定位置删除数据
void SeqListErase(SeqList* ps, int pos)
{
	assert(ps);
	assert(pos >= 0 && pos < ps->size);

	for (int i = pos; i < ps->size - 1; i++)
	{
		ps->a[i] = ps->a[i + 1];
	}

	--ps->size;
}

        这样在添加了这两个文件后就可以对顺序表实现各种对数据的操作了。

四.总结

        顺序表是一种存储数据的有效方式，但其中存在频繁的申请内存空间，多次进行扩容，可能会造成空间浪费，同时在指定位置插入与删除时间复杂度均为O(n)，但后续的链表可以解决上述的空间问题，下一期我们将介绍链表，并讨论它是如何实现，解决空间的浪费问题的。

ll778811
关注
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值