切原木问题（动态规划法）

题目

给定一根长度为N米的原木；另有一个分段价格表，给出长度L1,L2,…Li,…Lk米所对应的价格P1,P2…Pk(Li，Pi均为正整数)，求切割原木分段出售所能获得的最大收益。 例如，根据下面给出的价格表，

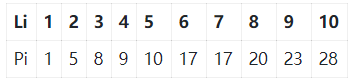
若要出售一段8米长的原木，最优解是将其切割为2米和6米的两段，这样可以获得最大收益=L2+L6=5+17=22。而若要出售一段3米长的原木，最优解是根本不要切割，直接售出。

输入格式:
首行输入N,k，紧接着第二行为k个Li（递增有序）和第三行对应的k个Pi值。 (0<N,k<1000) 。

输出格式:
对应原木的最大切割收益(题目中保证最大收益值在int范围)。

输入样例:
在这里给出一组输入。例如：

8 10
1 2 3 4 5  6  7  8  9  10
1 5 8 9 10 17 17 20 23 28

输出样例:
在这里给出相应的输出。例如：

22

答案

#include<bits/stdc++.h>
using namespace std;
int main()
{
	int num,n;
	cin>>num>>n;
	int len[n],cost[n],dp[n];
	fill(dp,dp+n,0);
	for(int i=0;i<n;i++)
	cin>>len[i];
	for(int i=0;i<n;i++)
	cin>>cost[i];
	for(int i=0;i<n;i++)
	{
		for(int j=len[i];j<=num;j++)
		dp[j]=max(dp[j],dp[j-len[i]]+cost[i]);
	}
	cout<<dp[num];
}

参考

切原木问题 (25分) (完全背包)