本文详细介绍了支持向量机（SVM）在处理线性可分数据时的优化问题。线性可分是指存在一条直线能将数据完全划分。最优分类直线需满足最大化间隔条件。在非线性情况下，引入松弛变量和惩罚系数C，通过拉格朗日乘数法转换为对偶问题。核函数用于解决非线性问题，例如高斯核和多项式核。对偶问题的求解利用了凸优化和强对偶性。关键词包括支持向量机、线性可分、优化问题、核函数和对偶问题。
线性可分定义
以二维为例，存在一条直线将其完全分开即为线性可分，否则线性不可分，如下图：
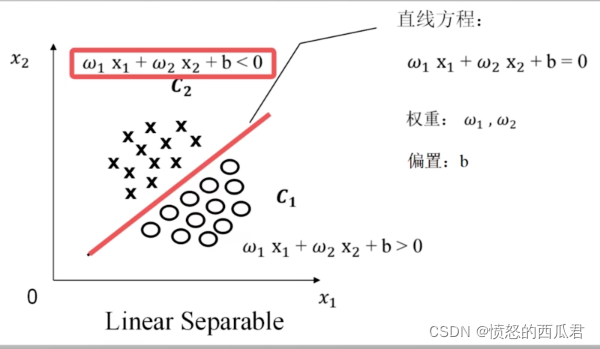
其中大于0还是小于0是人为规定的，就像上面的w1、w2、b我都取个相反数就大于变小于，小于变大于了。
n个训练样本为X1到Xn，至于为什么把Xi分为Xi1和Xi2，因为这也是二维的，看看第一个二维坐标系的图就理解了。yi取+1和-1也是人为定义的，当然也可以取其他值，但是这样可以对整个式子做一个统一简化（后面会有）。
最优分类直线
在线性可分的条件下，有且只有唯一一条直线，满足上面三个条件
优化问题
首先给个定义：
解释：
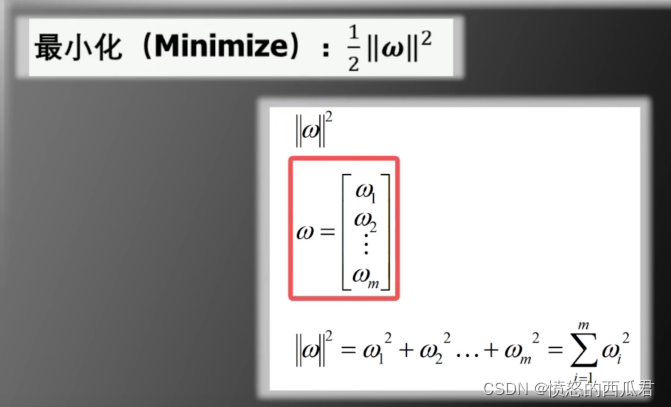
这里其实我还有点疑惑为什么要加一个1/2的系数，可能后面有别的用处吧先放着。
非线性可分情况时，无解，此时需要放松限制条件，如下：
C是比例因子，是人为设置的（算法的超参数）
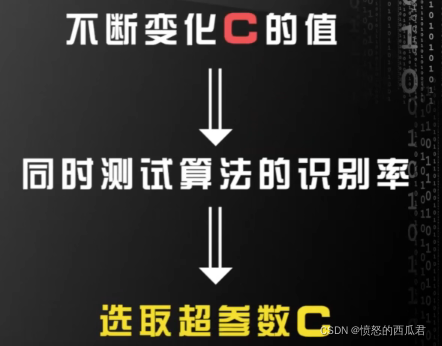
定理：
维度增高算法还是类似的。
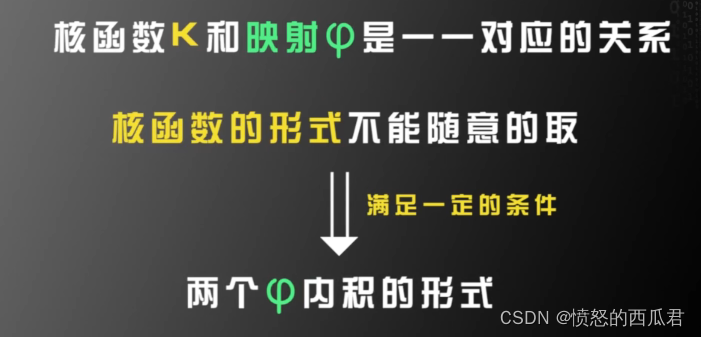
核函数
两个例子：
图上有点问题，但算式没错按算式理解就好。
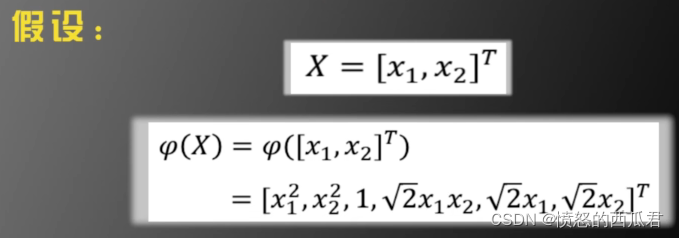
原问题和对偶问题
对偶差距大于等于0
简单理解如下：
转化为对偶问题
将支持向量机的优化问题进行改造
这两个限制条件都是线性的，而支持向量机的目标函数是凸的满足强对偶定理。
再看一下原问题的定义，也就是说有两个gi没有hi
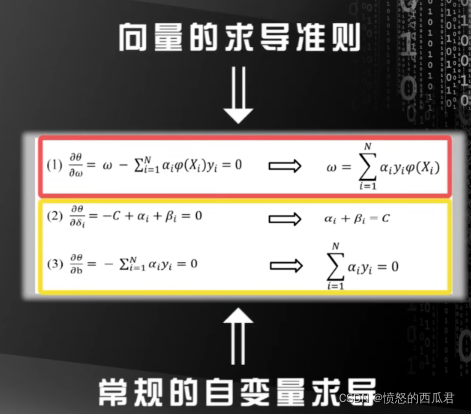
化简得：
如何求解这个对偶问题？
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
