DataWhale

Information Theory Basis

• Entropy
  The entropy $H(x)$ of a discrete random variable $X$ with distribution $p(x)$ is defined by $$H(X)=-\sum _{x\in \chi }p(x)logp(x)$$

• Joint Entropy
  The joint entropy $H(X,Y)$ of a pair of discrete random variables $(X,Y)$ with a joint distribution $p(x,y)$ is defined as $$H(X,Y)=-\sum _{x\in \mathcal{X}}\sum _{y\in \mathcal{Y}}p(x,y)logp(x,y)$$

• Conditional Entropy
  The conditional entropy $H(Y|X)$ of a pair of discrete random variables $(X,Y)$ with a joint distribution $p(x,y)$ is defined as $$H(Y|X)=-\sum _{x\in \mathcal{X}}\sum _{y\in \mathcal{Y}}p(x,y)logp(y|x)$$

• Information Gain
  The information gain $G(X)$ is defined as $$G(X)=H(Y)-H(Y|X)$$ which represents the importance of condition $X$ for the entropy $H(Y)$.

• Gini impurity
  The gini impurity a error rate to check whether a set of data belongs to the same category which is defined as $$I_G(f)=\sum _{i=1}^m{f}_i(1-f_i)$$
  Smaller it is, more likely the set of data is the same category.

Decision Tree

Different classification algorithms

• ID3 algorithm
  For the same output class $D_i$, computes the information gain $A_g$ of every feature and find the maximum one. Then for each value in $A_g$, find the different output classes $D_i$ and repeat again if the maximum $A_g$ is more than the threshold $ϵ$.
  This algorithm is used for discrete features.

• C4.5 algorithm
  It has the same principle as ID3, and overcomes the four disadvantages in ID3:

  1. no consideration for continuous features
  2. different number of value in each feature can affect the result
  3. no consideration for the situation when there is a missing value in a feature
  4. no consideration for overfitting

     solution for overfitting:
     regularization for preliminary pruning

• CART algorithm(classification and regression tree)

  1. the gini value would be the basis of node splitting for a classification tree
  2. the minimum variance of sample would be the basis of node splitting for a regression tree

Model evaluation

There are classifier and regression evaluation index for the classification and regression tree, respectively.

• auc and roc curve
• RMSE & quantiles of errors

note: more index referring previous article

The sklearn parameters

sklearn.tree.DecisionTreeClassifier(criterion='gini', splitter='best', max_depth=None, min_samples_split=2,min_samples_leaf=1, max_features=None, random_state=None, min_density=None, compute_importances=None,max_leaf_nodes=None)

• criterion: feature splitting method(‘gini’ or ‘entropy’)
• max_depth: the maximum depth of the decision tree, and overcome overfitting
• min_samples_leaf: the minimum number of sample included in leaf node

Code to draw decision tree:

# coding=utf-8

# sklearn中为我们准备的数据-iris
# iris有三种鸢尾花，山鸢尾花，变色鸢尾和维吉尼亚鸢尾
# 数据中有4个特征（feature）
# sepal length (花萼长度)
# sepal width (花萼宽度)
# petal lenth (花瓣长度)
# petal width (花瓣宽度)
from sklearn.datasets import load_iris
from sklearn import tree
import numpy as np

# 获取鸢尾数据
iris = load_iris()

# 用来做测试的数据下标
test_idx = [0,50,100]

# 用以训练的数据
train_target = np.delete(iris.target,test_idx)
train_data = np.delete(iris.data,test_idx,axis=0)

# 用以测试的数据
test_target = iris.target[test_idx]
test_data = iris.data[test_idx]


# 决策树
clf = tree.DecisionTreeClassifier()
clf.fit(train_data,train_target)

# 打印出测试数据和决策树的预言数据
# 结果应该是一样的（即决策树能正确预测）
print ("test_target:")
print (test_target)
print ("predict:")
print (clf.predict(test_data))


# 将决策树可视化
# 需要pydot(我安装了兼容版本pydotplus)
# 同时需要Graphviz(请去官网www.graphviz.org下载)
from sklearn.externals.six import StringIO
import pydotplus

dot_data = StringIO()
tree.export_graphviz(clf,
                        out_file=dot_data,
                        feature_names=iris.feature_names,
                        class_names=iris.target_names,
                        filled=True,rounded=True,
                        impurity=False)

graph = pydotplus.graph_from_dot_data(dot_data.getvalue())
# 输出pdf，显示整个决策树的思维过程
graph.write_pdf("viz.pdf")

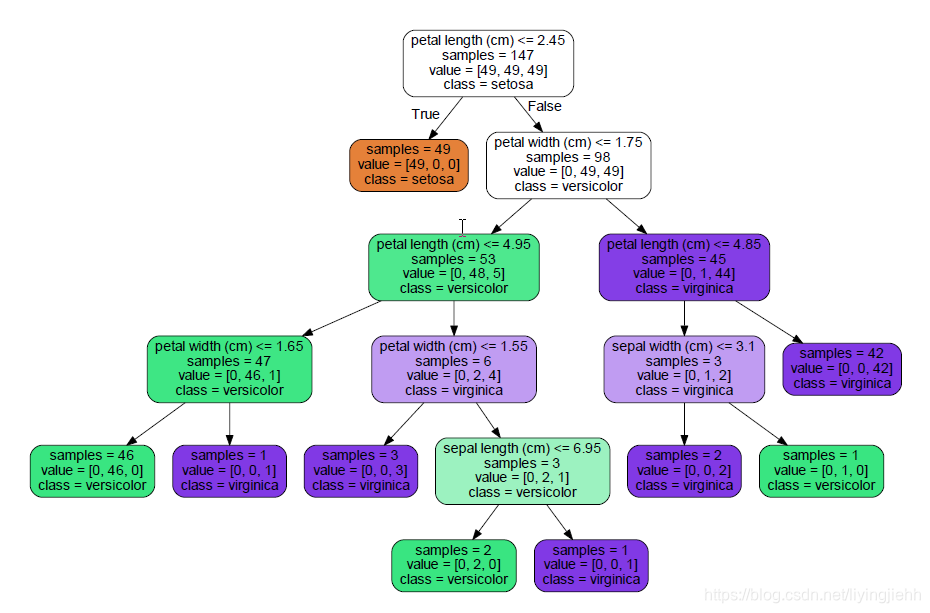
the decision tree is :

Reference

[1] http://blog.51cto.com/12482328/2105558

[2] https://blog.youkuaiyun.com/lanchunhui/article/details/51140053

[3] http://www.cnblogs.com/pinard/p/6050306.html

[4] https://www.jianshu.com/p/498ea0d8017d

[5] https://www.cnblogs.com/AlwaysT-Mac/p/6647192.html