高级分类器：支持向量机( SVM)与凸优化

前几篇博文分别介绍了一些逻辑回归与决策树以及神经网络的实战案例
数据挖掘实战案例——客户细分

数据挖掘实战实例——信用评级

机器学习实例——信用评级全流程实现

机器学习实战——使用决策树进行初始信用评级

机器学习实战——使用神经网络进行客户流失预警

现在我们来研究研究支持向量机
同样是实战案例
具体代码与数据集可访问下面的GitHub地址

GitHub地址

读取数据集

%matplotlib inline
import os
import numpy as np
from scipy import stats
import pandas as pd
import sklearn.model_selection as cross_validation
import matplotlib.pyplot as plt
orgData = pd.read_csv('date_data2.csv')
orgData.describe()

提取如下字段进行建模

X = orgData.ix[:, :4]
Y = orgData['Dated']

构建训练集和测试集

train_data, test_data, train_target, test_target = cross_validation.train_test_split(
    X, Y, test_size=0.4, train_size=0.6, random_state=123)   #划分训练集和测试集

使用svm，建立支持向量机模型

from sklearn import svm

svcModel = svm.SVC(kernel='rbf', gamma=0.5, C=0.5, probability=True).fit(train_data, train_target)

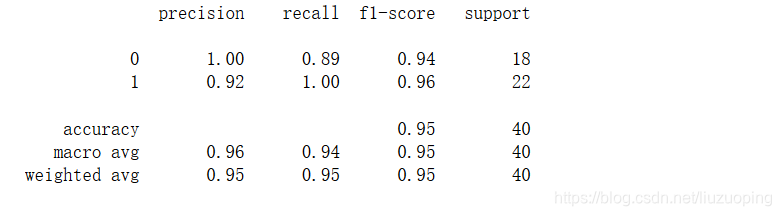
初步评估

import sklearn.metrics as metrics

test_est = svcModel.predict(test_data)
print(metrics.classification_report(test_target, test_est))  # 计算评估指标

进行标准化提升高斯核svm的表现

from sklearn import preprocessing

scaler = preprocessing.StandardScaler().fit(train_data)
train_scaled = scaler.transform(train_data)
test_scaled = scaler.transform(test_data)

svcModel1 = svm.SVC(kernel='rbf', gamma=0.5, C=0.5, probability=True).fit(train_scaled, train_target)
test_est1 = svcModel1.predict(test_scaled)
print(metrics.classification_report(test_target, test_est1))  # 计算评估指标

选择最优模型

from sklearn.model_selection import ParameterGrid, GridSearchCV

kernel = ('linear', 'rbf')
gamma = np.arange(0.01, 1, 0.1)
C = np.arange(0.01, 1.0, 0.1)
grid = {'gamma': gamma, 'C': C}

clf_search = GridSearchCV(estimator=svcModel1, param_grid=grid, cv=4)
clf_search.fit(train_scaled, train_target)

best_model = clf_search.best_estimator_
test_est2 = best_model.predict(test_scaled)
print(metrics.classification_report(test_target, test_est2))  # 计算评估指标

画出在svm模型中，两个变量的关系图，可以用于提升感性认识，但一般不能推广到大于两维的情况

train_x = train_scaled[:, 1:3]
train_y = train_target.values
h = 1.0  # step size in the mesh
C = 1.0  # SVM regularization parameter
svc = svm.SVC(kernel='linear', C=C).fit(train_x, train_y)
rbf_svc = svm.SVC(kernel='rbf', gamma=0.5, C=1).fit(train_x, train_y)
poly_svc = svm.SVC(kernel='poly', degree=3, C=C).fit(train_x, train_y)
lin_svc = svm.LinearSVC(C=C).fit(train_x, train_y)

# create a mesh to plot in
x_min, x_max = train_x[:, 0].min() - 1, train_x[:, 0].max() + 1
y_min, y_max = train_x[:, 1].min() - 1, train_x[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))

# title for the plots
titles = ['SVC with linear kernel',
          'LinearSVC (linear kernel)',
          'SVC with RBF kernel',
          'SVC with polynomial (degree 3) kernel']
plt.figure(figsize=(8, 8))
for i, clf in enumerate((svc, lin_svc, rbf_svc, poly_svc)):
    # Plot the decision boundary. For that, we will assign a color to each
    # point in the mesh [x_min, x_max]x[y_min, y_max].
    plt.subplot(2, 2, i + 1)
    plt.subplots_adjust(wspace=0.2, hspace=0.2)

    Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])

    # Put the result into a color plot
    Z = Z.reshape(xx.shape)
    plt.contourf(xx, yy, Z, cmap=plt.cm.coolwarm, alpha=0.7)

    # Plot also the training points
    plt.scatter(train_x[:, 0], train_x[:, 1], c=train_y, cmap=plt.cm.coolwarm)
    plt.xlabel('Attractive')
    plt.ylabel('Assets')
    plt.xlim(xx.min(), xx.max())
    plt.ylim(yy.min(), yy.max())
    plt.xticks(())
    plt.yticks(())
    plt.title(titles[i])

plt.show()