KM算法讲解（含C++代码）

最新推荐文章于 2025-05-02 22:58:09 发布

原创

最新推荐文章于 2025-05-02 22:58:09 发布 · 3.9k 阅读

14 ·

CC 4.0 BY-SA版权

本文介绍了KM算法的应用，通过一个婚姻匹配的例子详细解释了算法的贪婪匹配过程，确保期望值之和最大。同时，提供了一个相关的模板题目，描述了在工作中分配任务以最大化效率的问题。文章末尾分享了C++代码实现，并邀请读者在评论区交流反馈。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

假设有3个女的要嫁给三个男的，各有各的期望值。
如何让期望值之和最大？
此时我们就要用到~~传说中的~~km算法了。
这个算法本质上是贪心算法，怎么算呢？
举个例子吧
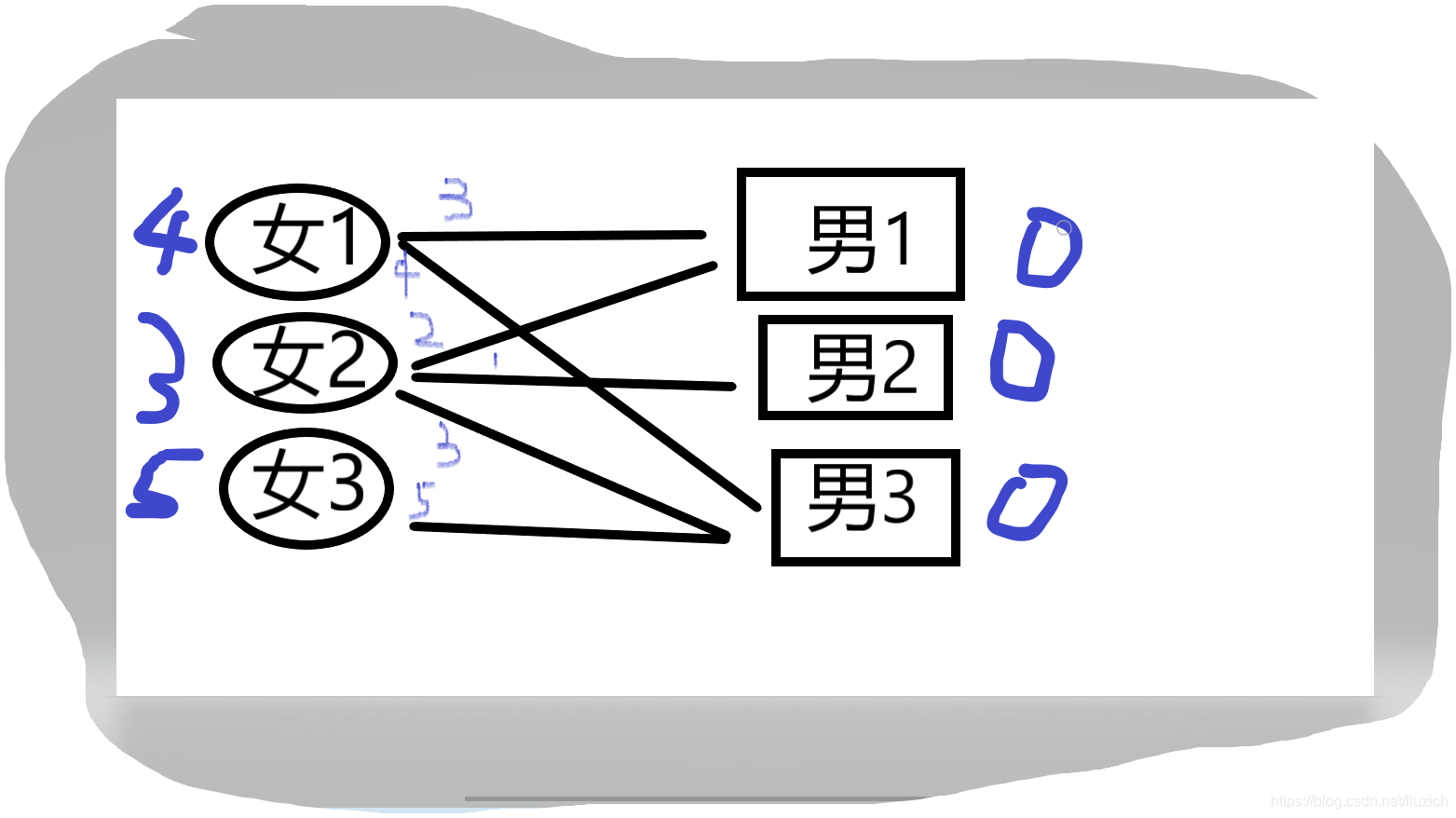
在这里插入图片描述
首先看女1，女1与男1间的边权值+男1期望值=3,而3不等于女一的期望值，所以配对失败。接着女1与男3间的边权值+男3的期望值=4，刚好4与女1的期望值相等，配对成功！

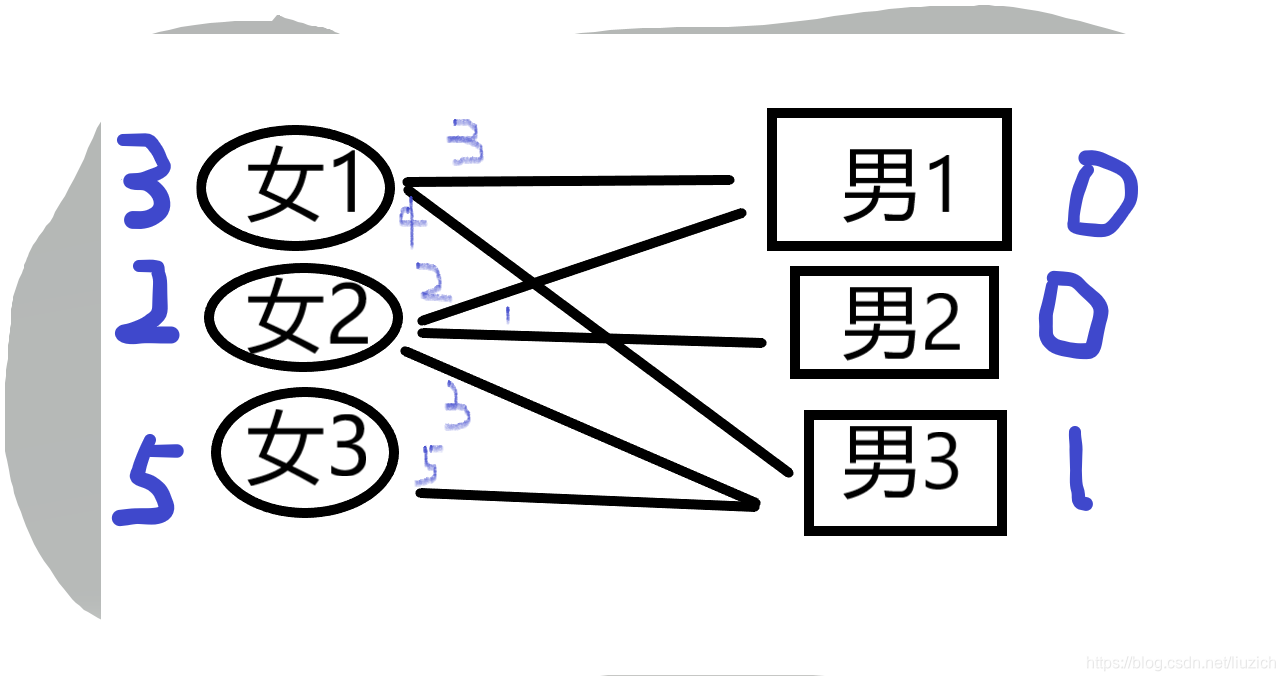
接着让女2找对象，匹配的过程就省略了，最后发现跟男3可以配对，而男3被女1占了，女2对女1说：“你能不能降低一下期望值啊？”于是女1同意了，但是我们还是得让女1跟男3可以配对，于是就将女1的期望值降低1，男3的期望值上升1，这样他们还是能够配对（男3挑剔了起来）。但是这样女2又不能配对了，就将女2的期望值也降低。这是发现女1可以和男1配对，就将他们配起来。
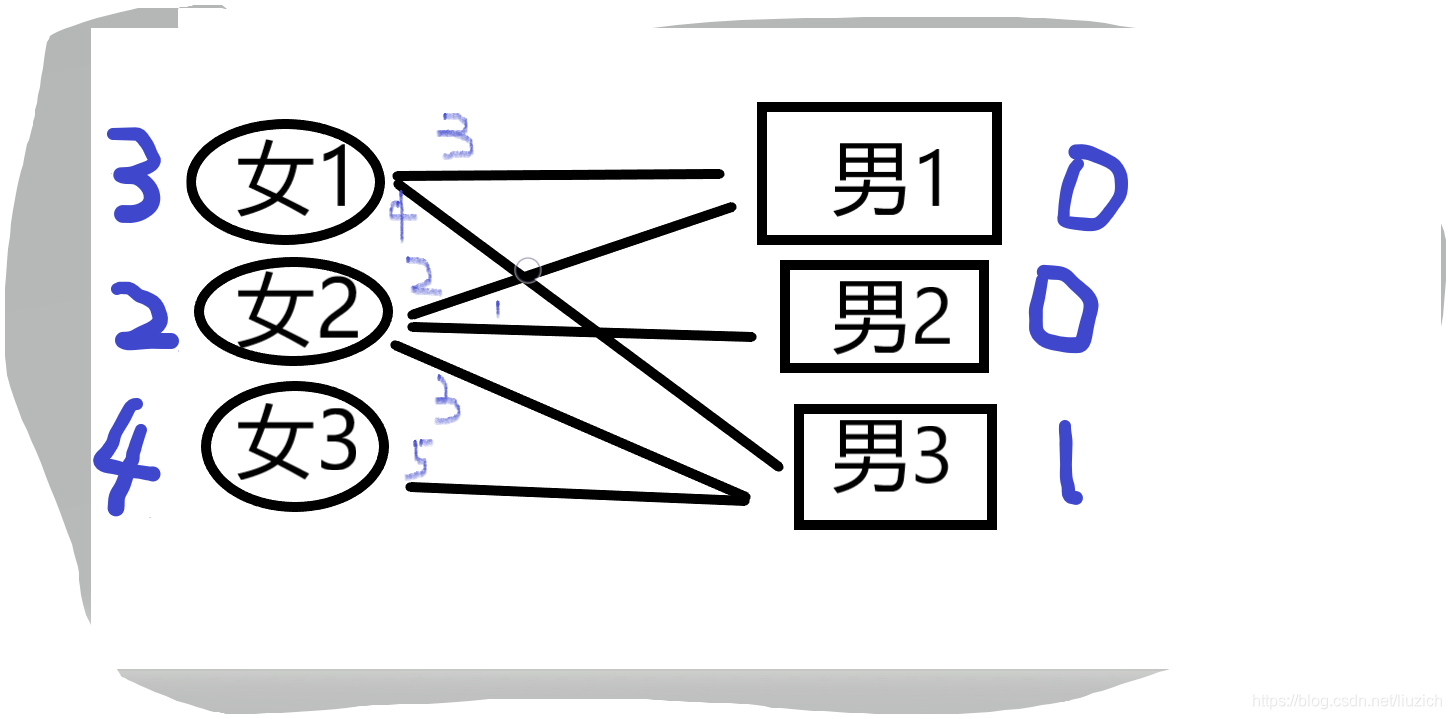
在这里插入图片描述
接着帮女3找对象，发现女3无法跟任何人配对，就只好将她的期望值降1，让她可以和男3配对。

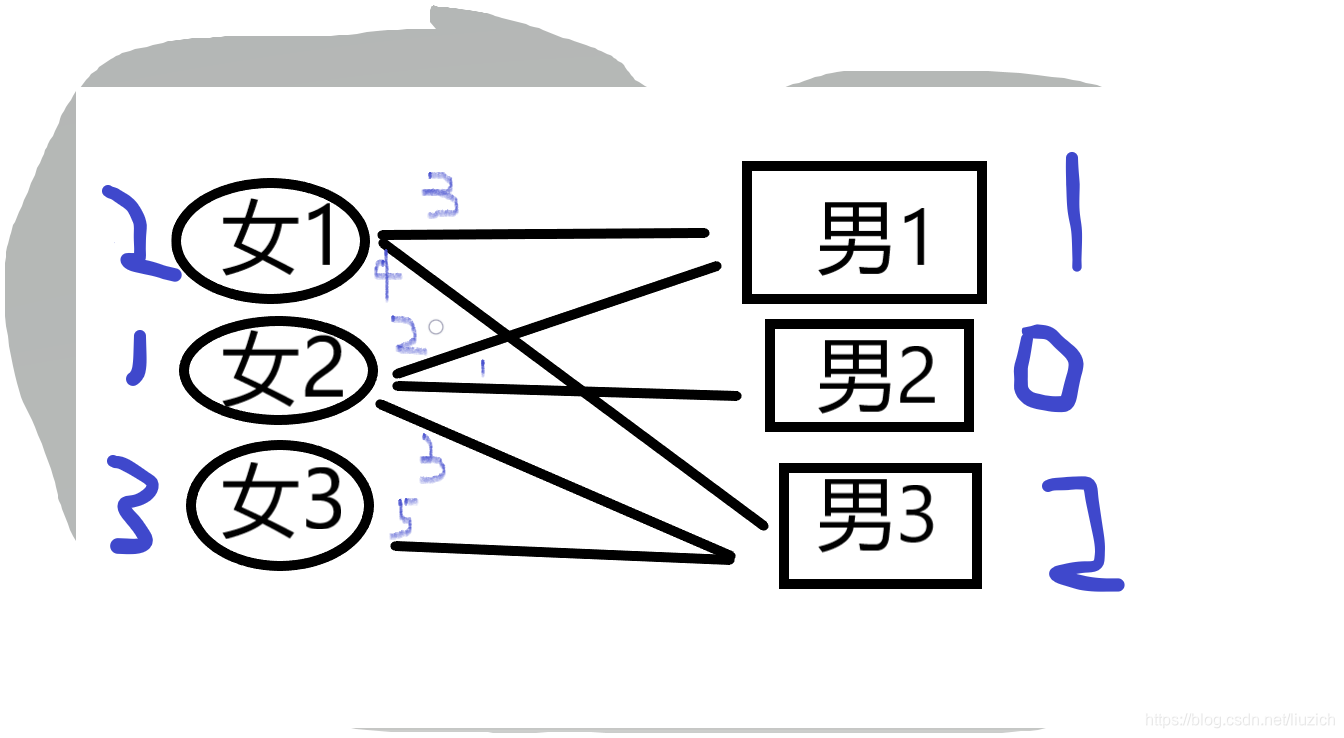
此时女3发现男3被女2占了，于是就勒索让女2降低期望值，于是女2降低1期望值，为了以后还能找男3，所以男3的期望值上升1，女3期望值也得随之降1。这时女1的期望值也得降低1，因为女1也要保持随时可以与男3配对。接着女2找上了男2，于是就跟男2配对。

此时三男三女都有了自己的对象了。~~（好开心，终于打完字了）~~

你以为这就结束了？
不可能，还有例题呢：

Description

小W在八中开了一个兼职中心。现在他手下有N个工人。每个工人有N个工作可以选择，于是每个人做每个工作的效率是不一样的。做为CEO的小W的任务就是给每个人分配一个工作，保证所有人效率之和是最大的。N<=200

Input

第一行给出数字N
接下来N行N列，代表每个人工作的效率。

Output

一个数字，代表最大效率之和

Sample Input

4
62 41 86 94
73 58 11 12
69 93 89 88
81 40 69 13

Sample Output

HINT

这就是km算法的模板题（虽然跟我举的例子有点出入，但本质上还是相同的）。
代码有点长，慢慢看啊
版本1：

#include<bits/stdc++.h>
using namespace std;
const int N=205;
int w[N][N];
int la[N],lb[N];
bool va[N],vb[N];
int match[N];
int delta,n;
void read() {
   
   
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            scanf("%d",&w[i][j]);
}
bool dfs(int x) {
   
   
    va[x]=1;
    for(int y=1;y<=n;y++)
        if(!vb[y])
            if(la[x]+lb[y]-w[x][y]==0) {
   
   
                vb[y