KingbaseAnalyticsDB 学习之madlib图计算能力

kadb在已经安装完maidlib扩展的情况下测试madlib.graph_sssp。

madlib.graph_sssp单源最短路径函数
        该函数使用Bellman-Ford算法实现。
（1）语法
graph_sssp( vertex_table,
            vertex_id,
            edge_table,
            edge_args,
            source_vertex,
            out_table
          )
（2）参数
        vertex_table：TEXT类型，包含图中顶点数据的表名。
        vertex_id：TEXT类型，缺省值为‘id’，vertex_table表中包含顶点的列名。顶点列必须是INTEGER类型，并且数据不能重复，但不要求连续。
        edge_table：TEXT类型，包含边数据的表名。边表必须包含源顶点、目标顶点和边长三列。边表中允许出现回路，并且构成回路的权重可以不同。
        edge_args：TEXT类型，是一个逗号分隔字符串，包含多个“name=value”形式的参数，支持的参数如下：
src （INTEGER）：边表中包含源顶点的列名，缺省值为‘src’。
dest （INTEGER）：边表中包含目标顶点的列名，缺省值为‘dest’。
weight （FLOAT8）：边表中包含边长的列名，缺省值为‘weight’。
        source_vertex：INTEGER类型，算法的起始顶点。此顶点必须在vertex_table表的vertex_id列中存在。
        out_table：TEXT类型，存储单源最短路径的表名，表中的每一行对应一个vertex_table表中的顶点，具有以下列：
vertex_id：目标顶点ID，使用vertex_id入参的值作为列名。
weight：从源顶点到目标顶点最短路径的边长合计，使用weight入参的值作为列名。
parent：在最短路径上，本顶点的上一节点，列名为‘parent’。

1. 创建测试表；

create table vertex(

id int

);

create table edge(

src int,

dest int,

weight float default 1.0

);

1. 导入测试数据；

gunzip amazon0601.txt.gz

注：解压的文件要去除头部信息。

copy edge(src,dest) from '/home/mppadmin/amazon0601.txt';

insert into vertex select vertex from (select distinct(src) as vertex from edge union select distinct(dest) as vertex from edge ) as x order by vertex;

1. 查找顶点所有邻居；

select src, concat(ts.set, td.set) from (select src, string_agg(dest::text, ',') as set from edge group by src) as ts,

(select dest, string_agg(src::text, ',') as set from edge group by dest) as td where src = dest limit 10;

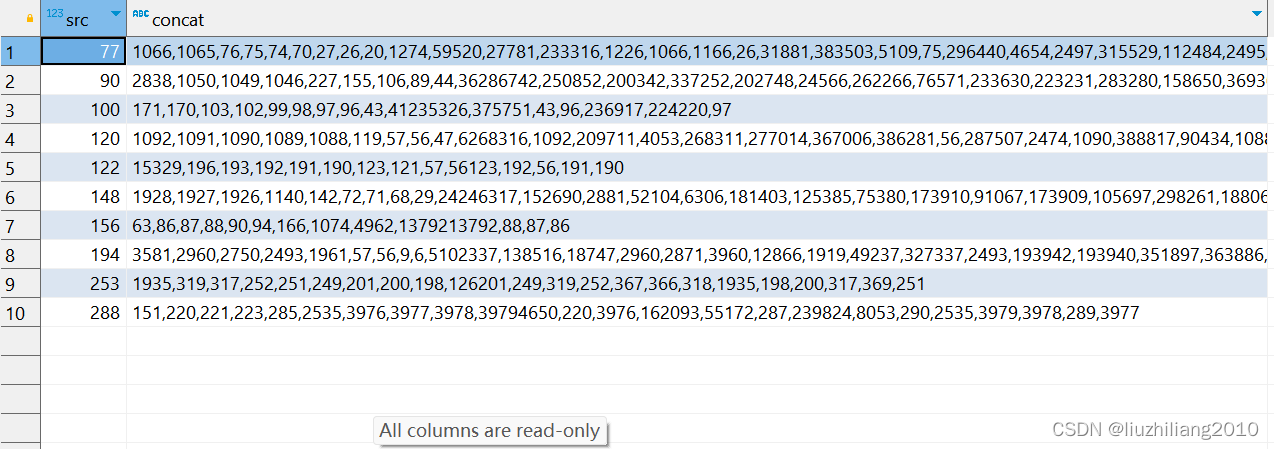
2.输出所有边的顶点；

select * from edge;

3.查找指定顶点和100个其他顶点间的最短路径；

create table spv as select * from vertex order by id limit 101;

select madlib.graph_sssp( 'spv', '', 'edge', '', 0, 'sssp', '');

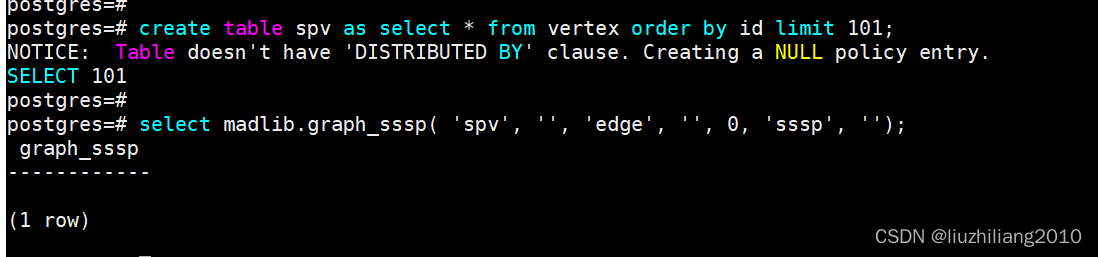
4.获取1-3度关系内全部顶点

degree = 1:

select distinct(dest) from edge where src = 0 union select distinct(src) from edge where dest = 0;

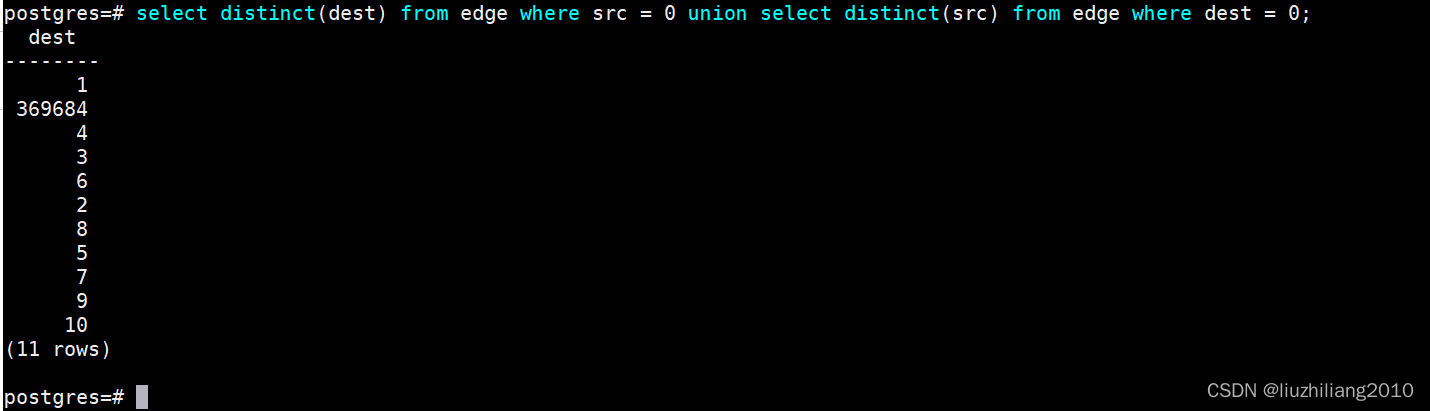
degree = 2:

with t (dest) as (select distinct(dest) from edge where src = 0 union select distinct(src) from edge where dest = 0) select distinct(dest) from edge where src in (select dest from t) union select distinct(src) from edge where dest in (select dest from t);

degree = 3:

with t (dest) as (with t (dest) as (select distinct(dest) from edge where src = 0 union select distinct(src) from edge where dest =0) select distinct(dest) from edge where src in (select dest from t) union select distinct(src) from edge where dest in (select dest from t))    select distinct(dest) from edge where src in (select dest from t) union select distinct(src) from edge where dest in (select dest from t);