冒泡排序和选择排序的区别

一、冒泡排序

冒泡排序的时间复杂度为O(n^2)，冒泡排序法是最简单基础的一种排序方法，但是它的时间复杂度较大，排序一组数组比较的次数较多。

• 冒泡排序的具体操作过程：

1. 比较相邻的元素。如果第一个比第二个大，就交换他们两个。

       2. 对每一对相邻元素做同样的工作，从开始第一对到结尾的最后一对。这一趟比较完后，最后的元素会是最大的数。

       3. 针对所有的元素重复以上的步骤，除了最后一个。（排好序的数不再进行比较）

       4. 持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

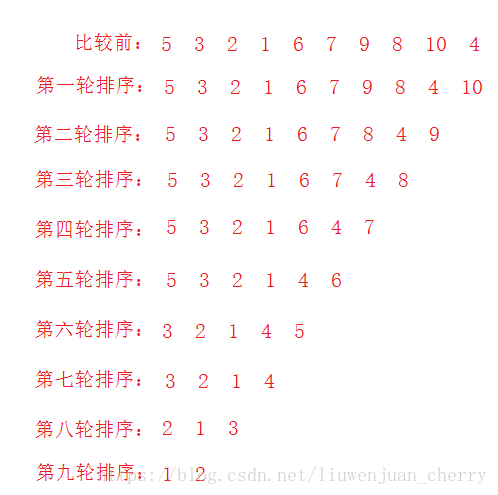
每一趟排序都会使最大的数交换到最后的位置上面。

void Bubble_sort(int *arr, int size)
{
       int i = 0;
       int j = 0;
       for (i = 0; i < size - 1; i++)//控制比较的趟数
       {
              for (j = 0; j < size - i - 1; j++)//控制每一趟需要比较的次数
              {
                     if (arr[j]>arr[j + 1])
                     {
                           int tmp = arr[j];
                           arr[j] = arr[j + 1];
                           arr[j + 1] = tmp;
                     }
              }
       }
}

冒泡排序的外层循环总共循环size-1次，内层循环总共循环size-i-1次，所以冒泡排序的时间复杂度为O(n^2)，它的空间复杂度为O（1）。

二、选择排序法

1. 将要排序的数组分成两个数组，一个是有序数组一个是无序数组，再定义一个最值和遍历下标
2. 假定有序数组是数组的第一个元素，这个最值也假定为数组的第一个数，遍历下标从第一个数开始
3. 然后将有序数组中的数和遍历下标指向的数进行比较， 如果无序数组中的数大于或小于有序数组中的数，那么将最大值或者最小值的下表更新为无序数组中那个值的下标
4. 然后再将新的最大值或者最小值的下标和有序数组中的数比较，若大于或者小于，那就将它们两的值进行交换。

void SelectSort(int *pSLD,int size)
{
       int minpos = 0;//将数组分为两个：有序数组和无序数组，将有序数组中的值和无序数组中的值比较，不断更新有序数组
       int i = 0;//有序数组的下标
       int j = 0;//无序数组的下标
       for (i = 0; i < size; i++)
       {
              minpos = i;
              for (j = i + 1; j <size; j++)
              {
                     if (pSLD[minpos] > pSLD[j])
                           minpos = j;
              }
              if (pSL[minpos] < pSLD[i])
                     Swap(&pSLD[i], &pSLD[minpos]);
       }
}

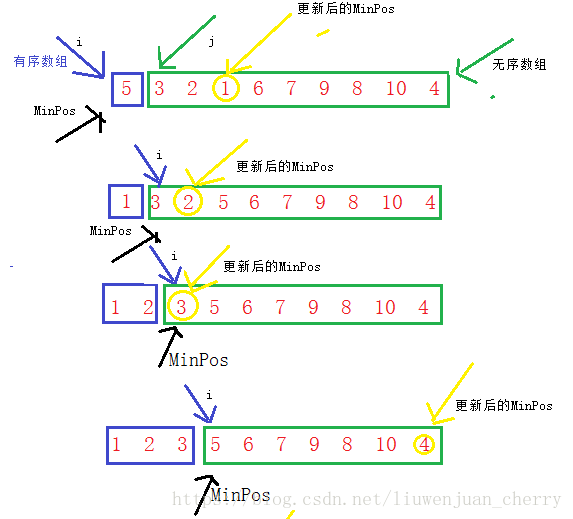
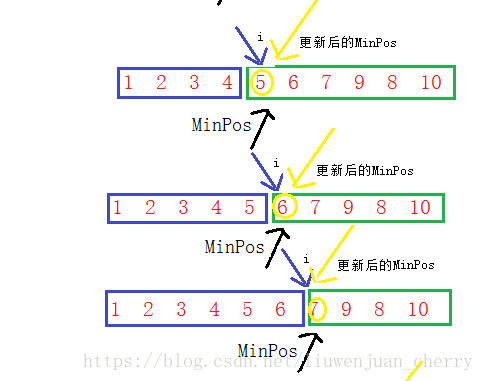
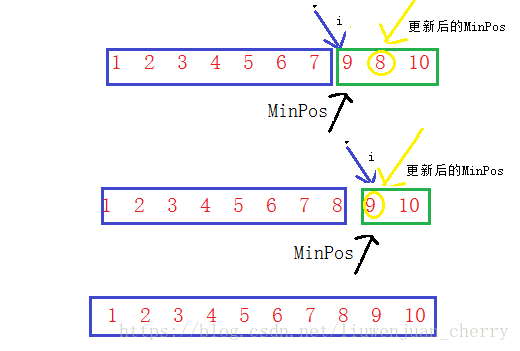
选择排序是每次从无序数组中选出最值，放到有序数组中，它的时间复杂度为O（n^2），空间复杂度为O(1)。