本文详细介绍了单调栈在解决每日温度问题中的应用，有效括号的验证方法，以及单调队列在求解队列最大值问题中的巧妙运用。此外，还探讨了栈和队列以及优先队列在处理滑动窗口最大值和数据流中第K大元素问题的解决方案，揭示了这些基础数据结构在算法设计中的重要性。
文章目录
单调栈算法
739. 每日温度（单调栈算法）
给定一个整数数组 temperatures ，表示每天的温度，返回一个数组 answer ，其中 answer[i] 是指在第 i 天之后，才会有更高的温度。如果气温在这之后都不会升高，请在该位置用 0 来代替。
class Solution {
public int[] dailyTemperatures(int[] temperatures) {
if (temperatures == null) {
return null;
}
int len = temperatures.length;
if (len <= 0) {
return null;
}
int[] res = new int[len];
// 从底向上 递增 的 单调栈
Stack<Integer> incrStack = new Stack<>();
for (int i = 0; i < temperatures.length; i++) {
while (!incrStack.isEmpty() && temperatures[i] > temperatures[incrStack.peek()]) {
// 计算 之前栈中堆积的元素的第 i 天数
res[incrStack.peek()] = i - incrStack.peek();
incrStack.pop();
}
// 还需要把当前的 index 推入 栈中
incrStack.push(i);
}
return res;
}
}
- 时间：O(n)
- 空间：O(n)
20. 有效的括号
https://leetcode-cn.com/problems/valid-parentheses/
class Solution {
public boolean isValid(String s) {
if (s == null) {
return false;
}
int n = s.length();
// 奇数直接返回 false
if ((n & 1) == 1) {
return false;
}
Map<Character, Character> pairs = new HashMap<Character, Character>() {{
put(')', '(');
put(']', '[');
put('}', '{');
}};
Stack<Character> stack = new Stack<>();
for (int i = 0; i < s.length(); i++) {
char ch = s.charAt(i);
if (pairs.containsKey(ch)) {
// 右 字符
if (stack.isEmpty() || stack.peek() != pairs.get(ch)) {
return false;
}
stack.pop();
} else {
//左字符 直接入栈
stack.push(ch);
}
}
return stack.isEmpty();
}
}
- 时间：O（n）
- 空间：O（n）
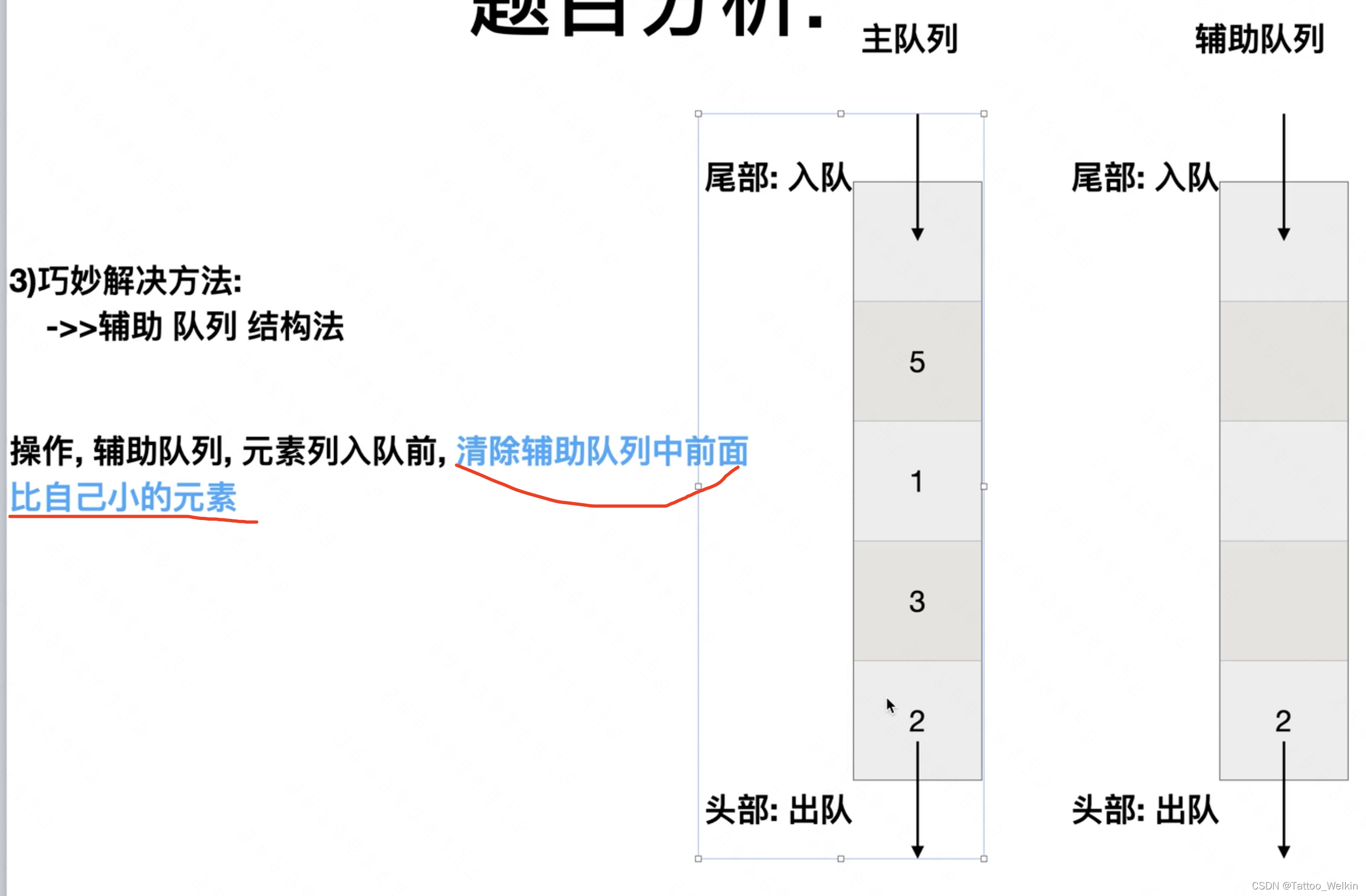
剑指 Offer 59 - II. 队列的最大值（单调队列类问题）
思路：
public class MaxQueue {
//主队列
Queue<Integer> queue;
//辅助队列
Deque<Integer> deque;
public MaxQueue() {
queue = new LinkedList<Integer>();
deque = new LinkedList<Integer>();
}
public int max_value() {
if (deque.isEmpty()) {
return -1;
}
//直接出队头即可
return deque.peekFirst();
}
public void push_back(int value) {
queue.offer(value);
//注意这里判断的是 last 即队尾
while (!deque.isEmpty() && deque.peekLast() <= value) {
deque.pollLast();
}
deque.offerLast(value);
}
public int pop_front() {
if (queue.isEmpty()) {
return -1;
}
int ans = queue.peek();
if (ans == deque.peekFirst()) {
deque.pollFirst();
}
return queue.poll();
}
public static void main(String[] args) {
MaxQueue obj = new MaxQueue();
int param_1 = obj.max_value();
int param_3 = obj.pop_front();
}
}
- 时间：O(1)
- 空间：> O(n)
栈和队列以及优先队列
1.栈的压入、弹出序列
输入两个整数序列，第一个序列表示栈的压入顺序，请判断第二个序列是否可能为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如序列1,2,3,4,5是某栈的压入顺序，序列4,5,3,2,1是该压栈序列对应的一个弹出序列，但4,3,5,1,2就不可能是该压栈序列的弹出序列。（注意：这两个序列的长度是相等的）
思路：
- 将 pushed 队列中的每个数都 push 到栈中，同时检查这个数是不是 popped 序列中下一个要 pop 的值，如果是就把它 pop 出来。
最后，检查不是所有的该 pop 出来的值都是 pop 出来了。时间复杂度O(n)，空间复杂度O(n)
class Solution {
public:
bool validateStackSequences(vector<int>& pushV, vector<int>& popV) {
if (pushV.empty() || popV.empty() || pushV.size() != popV.size())
return true;
std::stack<int> QQ;
int index = 0;
// 遍历的是 push 序列
for (const auto &it : pushV)
{
QQ.push(it);
//栈不空 数组下标不越界 （如果不相等就继续把 push 序列的数字压入栈中）
while (!QQ.empty() && index < pushV.size() && QQ.top() == popV[index])
{
QQ.pop();
index++;
}
}
return index == pushV.size();
}
};
2. 返回滑动窗口中的最大值
https://leetcode-cn.com/problems/sliding-window-maximum/
解法一：
使用优先队列，维护一个k个元素的 大顶堆（Java中是使用一个完全二叉树实现）。
public class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
if (nums == null || k <= 0 || nums.length <= 0) {
return null;
}
// 创建一个大顶堆，需要自定义比较器
PriorityQueue<Integer> priorityQueue = new PriorityQueue<Integer>(k, new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return o2 - o1;
}
});
for (int i = 0; i < k; i++) {
priorityQueue.add(nums[i]);
}
int[] result = new int[nums.length - k + 1];
result[0] = priorityQueue.peek();
// 每轮要移除的元素(滑动窗口最左边的一个元素,注意是 nums[0],而不是 队列首元素)
int last = nums[0];
for (int i = k; i < nums.length; i++) {
// 移除滑动窗口之外的元素
priorityQueue.remove(last);
// 添加新元素
priorityQueue.add(nums[i]);
// 取优先队列的最大首元素
result[i - k + 1] = priorityQueue.peek();
// 记录每轮要移除的元素（滑动窗口最左边的元素）
last = nums[i - k + 1];
}
return result;
}
}
- 时间复杂度：O(nlogn)，其中 nn 是数组 \textit{nums}nums 的长度。在最坏情况下，数组 \textit{nums}nums 中的元素单调递增，那么最终优先队列中包含了所有元素，没有元素被移除。由于将一个元素放入优先队列的时间复杂度为 O(\log n)O(logn)，因此总时间复杂度为 O(n \log n)O(nlogn)。
- 空间复杂度：O(n)O(n)，即为优先队列需要使用的空间。这里所有的空间复杂度分析都不考虑返回的答案需要的 O(n)O(n) 空间，只计算额外的空间使用。
解法二：
使用一个双端队列
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
if (nums == null || k <= 0 || nums.length <= 0) {
return null;
}
Deque<Integer> deque = new LinkedList<Integer>();
for (int i = 0; i < k; i++) {
// 双向队列 保存当前窗口最大值的数组位置 保证队列中数组位置的数值按从大到小排序
while (!deque.isEmpty() && nums[i] >= nums[deque.peekLast()]) {
deque.pollLast();
}
//数组下标：放到双端队列最后
deque.offerLast(i);
}
int[] result = new int[nums.length - k + 1];
// 取队列的最大首元素
result[0] = nums[deque.peekFirst()];
for (int i = k; i < nums.length; i++) {
while (!deque.isEmpty() && nums[i] >= nums[deque.peekLast()]) {
deque.pollLast();
}
deque.offerLast(i);
while (deque.peekFirst() <= i - k) {
deque.pollFirst();
}
result[i - k + 1] = nums[deque.peekFirst()];
}
return result;
}
}
-
时间复杂度：O(n)O(n)，其中 nn 是数组 \textit{nums}nums 的长度。每一个下标恰好被放入队列一次，并且最多被弹出队列一次，因此时间复杂度为 O(n)O(n)。
-
空间复杂度：O(k)O(k)。与方法一不同的是，在方法二中我们使用的数据结构是双向的，因此「不断从队首弹出元素」保证了队列中最多不会有超过 k+1k+1 个元素，因此队列使用的空间为 O(k)O(k)。
3. 返回数据流中的第K大元素
思路：
class KthLargest {
PriorityQueue<Integer> pq;
final int k;
public KthLargest(int k, int[] nums) {
this.k = k;
pq = new PriorityQueue<Integer>();
for (int x : nums) {
add(x);
}
}
public int add(int val) {
//如果还不是一个K的最小堆的话，就先添加上去，直接返回堆顶
if (pq.size() < k) {
pq.add(val);
}
// 现在绝对是一个K的最小堆，那么按照逻辑判断即可
else if(val > pq.peek()){
pq.poll();
pq.add(val);
}
return pq.peek();
}
}
- 时间复杂度：O(n*log(k))
- 空间复杂度：O(k)
扫一扫
2978
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
