图

1.图的介绍

图是一种数据结构，其节点可以有零个或多个相邻的元素，两个节点相连称为边。
顶点（也就是节点）vertex
边edge
路径
无向图：顶点之间的连接没有方向
有向图：顶点之间的连接有方向
带权图：边上带有权值，也叫网。
图的表示方式
邻接矩阵（二维矩阵）

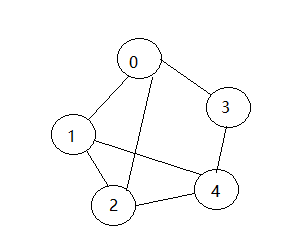
邻接矩阵为

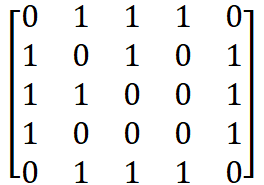
邻接表
邻接表只关心存在的边，相较于邻接矩阵而言不关心不存在的边，因此没有空间的浪费，邻接表由数组和链表组成。

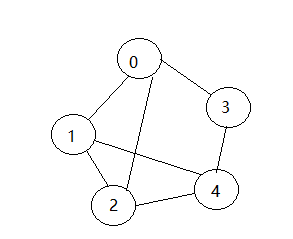
邻接表为

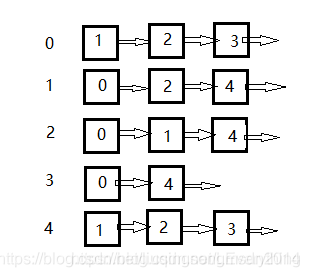
标号为0的节点相关联节点为1，2，3；。。。。。

一 图数据类型

邻接矩阵存储

typedef VTYPE int;

typedef struct
{
	VTYPE v[N];
	int matrix[N][N];
}Graph;

Graph *create_graph()
{
	G = 分配空间
	初始化顶点
	for(i = 0; i < N;i ++)
	{
		G->v[i] = i;
	}

	return G;
}


int input_edge(Graph *G)
{
	int i = 0,j = 0;

	//(V0,V1) (V0,V2) .... a
	while(scanf("(V%d,V%d)",&i,&j) == 2)
	{
		//吃掉空格字符
		getchar();
		G->matrix[i][j] = G->matrix[j][i] = 1;
	}

	//吃掉非法字符
	while(getchar() != '\n');

	return 0;
}

//输出顶点和邻接矩阵
void printf_graph(Graph *G)
{

}

2.图 instance analysis

#include <stdio.h>
#include <string.h>
#include <stdlib.h>

#define N 5

typedef int VTYPE;

typedef struct 
{
	VTYPE v[N];
	int matrix[N][N];
}Graph;

Graph *create_graph()
{
	int i = 0;
	Graph *G;

	G = (Graph *)malloc(sizeof(Graph));
	memset(G,0,sizeof(Graph));

	for(i = 0;i < N;i ++)
	{
		G->v[i] = i;
	}

	return G;
}

int input_edge(Graph *G)
{
	int i,j;
	
	//(V0,V1) (V0,V2) ... a
	while(scanf("(V%d,V%d)",&i,&j) == 2)
	{
		//吃掉空格字符
		getchar();
		G->matrix[i][j] = G->matrix[j][i] = 1;
	}
	
	//吃掉非法字符
	while(getchar() != '\n');

	return 0;
}

int printf_graph(Graph *G)
{
	int i,j;

	for(i = 0;i < N;i ++)
	{
		printf("V%d ",G->v[i]);
	}
	printf("\n");

	for(i = 0;i < N;i ++)
	{
		for(j = 0;j < N;j ++)
		{
			printf("%d ",G->matrix[i][j]);
		}
		printf("\n");
	}

	return 0;
}

int main(int argc, const char *argv[])
{
	Graph *G = create_graph();

	printf("Input edge : ");
	input_edge(G);

	printf_graph(G);
	
	return 0;
}

https://zhuanlan.zhihu.com/p/240717040
https://zhuanlan.zhihu.com/p/74472146