CSP考级辅导NOIP竞赛辅导专题计算机等级考试辅导提高组普及组复赛辅导计划
资料目录：
https://download.youkuaiyun.com/download/liuning940307/89319041目录：
1 各类数据范围
1.1 0x3F3F3F3F的来源
1.2 数组可以开多大
2 优化技巧
3 并查集
3.1 模板
3.2 练习题
4 链式前向星
5 STL
5.1 栈、队列、优先队列、双端队列
5.2 map容器
5.3 string操作
5.4 vector向量
5.5 set
6 贪心算法
6.1 活动安排问题
6.2 最小区间覆盖问题
6.3 练习题
7 归并排序
7.1 归并排序求逆序数
8 前缀和
8.1 简介
8.2 题目
9 差分数组
9.1 定义
9.2 性质
9.3 例题
10 树状数组
10.1 简介
10.2 实现
10.3 树状数组扩展
10.4 二维树状数组
10.5 题目练习
10.6 总结
11 字典树
11.1 字典树可以解决的问题
11.2 一题入门
11.3 练习题
12 DP入门
13 DP强化
13.1 钱币找零问题
14 二进制优化DP
15 单调队列优化DP
16 多路DP
16.1 例题
17 区间DP
18 数位DP
19 二分答案
20 二进制操作
21 状态压缩DP
22 树形DP
23 期望/概率DP
23.1 概率模型
23.2 入门题目
23.3 赠券收集问题
23.4 概率/期望DP-高难度
24 DP优化总结
25 单调栈
25.1 简介
25.2 应用
25.3 练习题
26 组合数学
26.1 N个球放入M个盒子问题
26.2 整数拆分
27 数论数学
27.1 逆序数
28 最优思想
28.1 无序数组的最大差值
29 数据结构
1、各类数据范围
1.1 0x3F3F3F3F的来源
（1）int类型的最大值:
MAX = 0x7fffffff; MIN = 0x8fffffff;
MAX = (1<<31) – 1; MIN = -(1<<31);
十进制：MAX 约为 2*10^9,如果超过了10^9,就需要long long存储。
用上述的方法表示最大和最小很多场景下不能使用，比如：
1）无穷大加一个常数还是无穷大的情况。
if(d[u] + w[u][v] < d[v]) d[v]=d[u]+w[u][v]; 最短路径算法的松弛操作。
2）无穷大加无穷大还是无穷大的情况。
如何解决？
很多人喜欢用0x3f3f3f3f来表示最大值，下面给出原因。
1）0x3f3f3f3f的十进制是1061109567，也就是10^9级别的（和0x7fffffff一个数量级），而一般场合下的数据都是小于10^9的，所以它可以作为无穷大使用而不致出现数据大于无穷大的情形。
2）由于一般的数据都不会大于10^9，所以当我们把无穷大加上一个数据时，它并不会溢出，这就满足了“无穷大加一个有穷的数依然是无穷大”，如果多个相加则这种方法也不可以，最好的方法是用某个东西代替无穷大，这又增加了编程难度。
3）如果我们想要将某个数组清零，我们通常会使用memset(a,0,sizeof(a))这样的代码来实现（方便而高效）。但是当我们想将某个数组全部赋值为无穷大时，就只能自己写循环来初始化，因为memset是按字节操作的，它能够对数组清零是因为0的每个字节都是0，现在我们将无穷大设为0x3f3f3f3f，0x3f3f3f3f的每个字节都是0x3f，所以要把一段内存全部置为无穷大，我们只需要memset(a,0x3f,sizeof(a))。
所以在通常的场合下，0x3f3f3f3f真的是一个非常棒的选择。
（2）long long最大值
MAX = (1<<63)-1; MIN = -(1<<63);
MAX = 9*10^18;
1.2 数组可以开多大
没有确切的答案，全局变量最好开10^6以内
int a[1000000];
有时候确定数组大小很麻烦
因此用vector是一个很好的选择。
2、输入优化
2 优化技巧
输入优化
https://blog.youkuaiyun.com/Lj_victor/article/details/81590816
3、并查集
并查集（Union/Find）从名字可以看出，主要涉及两种基本操作:合并和查找。初始时并查集中的元素是不相交的，经过一系列的基本操作(Union)，最终合并成多个集合。
在每次合并之前，或者合并之后，最基本的就是判断两个元素是否在一个集合中，这就涉及到查找操作。
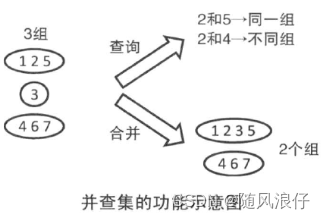
模板：
（1）简单并查集
int f[MAXN]; //并查集数组
//查询节点属于哪个集合
int find(int x){
while(f[x] != x){//一直找到根
x = f[x];
}
return x;
}
//合并两个节点,合并前需要自己判断是否属于同一集合
void merge(int x,int y) {
x = find(x);
y = find(y);
f[x] = y;
}
//main函数中需要进行初始化
for(int i = 1; i <= n; i++)
f[i] = i; //开始是各个节点成一个集合
对应上图来理解。
（2）启发式合并+路径压缩优化
int find(int x){
int temp = x;//保存子节点，为路径压缩使用
while(f[x] > 0){//一直找到根
x= f[x];
}
//路径压缩
int t;
while(temp != x){
t = f[temp];
f[temp] = x;
temp = t;
}
return x;
}
void union(int x,int y) {
int fx = find(x);
int fy = find(y);
if(fx != fy){
//启发式合并，少的往多的合并
if(-f[fx] < -f[fy]){
f[fy] += f[fx];
f[fx] = fy;
}else{
f[fx] += f[fy];
f[fy] = fx;
}
}
}
练习题：
入门级：
HDU1232畅通工程
Kruscal 最小生成树算法
POJ 1182 食物链
https://blog.youkuaiyun.com/niushuai666/article/details/6981689
并查集+DP：
http://blog.youkuaiyun.com/acm_cxlove/article/details/8092799
高级：
NOIP2010提高组关押罪犯 自己敌人的敌人与自己合并。
[NOI2001]食物链
带权并查集、映射并查集、种类并查集、异或并查集
HDU 3172 Virtual Friends
4、链式前向星
前向星是以存储边的方式来存储图，先将边读入并存储在连续的数组中，然后按照边的起点进行排序，这样数组中起点相等的边就能够在数组中进行连续访问了。它的优点是实现简单，容易理解，缺点是需要在所有边都读入完毕的情况下对所有边进行一次排序，带来了时间开销，实用性也较差，只适合离线算法。
图一般有两种存储方式，邻接矩阵和邻接表；其中邻接表用链表存储的话如下所示。
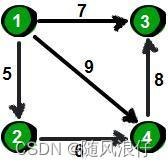
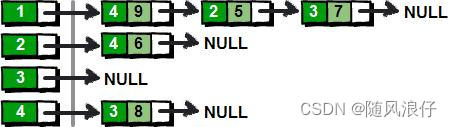
对于不喜欢使用链表的同学，可以使用数组模拟链表实现邻接表，基本思想是一致的。
链式前向星和邻接表类似，也是链式结构和线性结构的结合，每个结点i都有一个链表，链表的所有数据是从i出发的所有边的集合（对比邻接表存的是顶点集合），边的表示为一个四元组(u, v, w, next)，其中(u, v)代表该条边的有向顶点对，w代表边上的权值，next指向下一条边。
具体的，我们需要一个边的结构体数组 edge[MAXM]，MAXM表示边的总数，所有边都存储在这个结构体数组中，并且用head[i]来指向 i 结点的第一条边。i节点剩下的边就通过next访问，直到访问到-1或0。
模拟一遍代码即可明白。
/********************start链式前向星***************/
const int MAXN = 101;
const int MAXM = 200;
struct Edge{
int next;//边指针，指向下一条边的内存地址
int u,v,w;
}edges[MAXM];
int head[MAXN], cnt = 1; //head[]=0时遍历完
void addEdge(int u,int v,int w){
//三二一法（三个设置值，两个更新指针，一个自增）
edges[cnt].u = u;
edges[cnt].v = v;
edges[cnt].w = w;
edges[cnt].next = head[u];
head[u] = cnt;
cnt++;
}
/********************end链式前向星*****************/
访问：
//得到节点1的所有边，到地址为0结束，到零结束的原因是head[MAXN]全
//局变量置为0了，自己赋成-1用-1判断也一样。
for(int i = head[1]; i != 0; i = edge[i].next) {
cout<<"1->"<<edge[i].v<<" "<<edge[i].w<<endl;
}
5、STL
5.1 栈、队列、优先队列、双端队列的实用
更多内容可下载PDF资料学习：https://download.youkuaiyun.com/download/liuning940307/89319041
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
