<think>我们将实现两个同型NumPy矩阵的对应元素相乘（逐元素乘法）。这种操作在NumPy中非常高效，可以直接使用运算符或函数实现。注意：两个矩阵必须具有相同的形状，否则会引发ValueError。对应元素相乘的数学定义：C[i,j]=A[i,j]*B[i,j]我们将提供两种方法：使用运算符*和使用np.multiply函数。同时，我们也会考虑广播机制（虽然题目要求同型，但广播机制允许在某些维度不同但可广播的情况下操作）。不过，题目要求同型矩阵，所以我们将重点放在同型上。此外，我们还会展示如何处理数据类型、避免不必要的复制以及进行原地操作。代码示例：</think>
要实现两个同型NumPy矩阵的对应元素相乘（逐元素乘法），有以下几种高效方法：
### 核心实现方法
```python
import numpy as np
# 创建示例矩阵
a = np.array([[1, 2, 3],
[4, 5, 6]])
b = np.array([[2, 3, 4],
[5, 6, 7]])
# 方法1: 使用 * 运算符
result_operator = a * b
# 方法2: 使用 np.multiply 函数
result_multiply = np.multiply(a, b)
# 方法3: 使用原地操作
a_original = a.copy() # 保留原始矩阵
a_original *= b # 原地修改a_original
# 输出结果
print("矩阵 A:\n", a)
print("矩阵 B:\n", b)
print("使用 * 运算符的结果:\n", result_operator)
print("使用 np.multiply 的结果:\n", result_multiply)
print("原地操作后的 a_original:\n", a_original)
```
### 数学原理
矩阵对应元素相乘（Hadamard积）的数学定义：
```
Cᵢⱼ = Aᵢⱼ × Bᵢⱼ (其中 i=1..m, j=1..n)
```
其中：
- A 和 B 是同维矩阵
- C 是结果矩阵，形状与A、B相同
### 高级用法
#### 1. 处理不同数据类型
```python
int_matrix = np.array([[1, 2], [3, 4]])
float_matrix = np.array([[0.5, 1.5], [2.5, 3.5]])
# 混合类型会自动提升为高级类型
result_mixed = int_matrix * float_matrix
print("混合数据类型结果 (float):\n", result_mixed)
# 强制指定结果类型
result_int = np.multiply(int_matrix, float_matrix, dtype=np.int32)
print("强制转换为整数的结果:\n", result_int)
```
#### 2. 处理布尔矩阵
```python
bool_a = np.array([[True, False], [True, True]])
bool_b = np.array([[False, True], [True, True]])
# 布尔矩阵逐元素相乘相当于逻辑AND
result_bool = bool_a * bool_b
print("布尔矩阵相乘 (逻辑AND):\n", result_bool)
```
#### 3. 带掩码的条件乘法
```python
data = np.array([[10, 20], [30, 40]])
mask = np.array([[1, 0], [0, 1]], dtype=bool) # True的位置才计算
# 只对mask为True的位置相乘
conditional_result = np.multiply(data, 5, where=mask)
print("带掩码的条件乘法结果:\n", conditional_result)
```
#### 4. 稀疏矩阵乘法
```python
# 使用稀疏矩阵节省内存
from scipy.sparse import lil_matrix
sparse_a = lil_matrix((3, 3))
sparse_a[0, 0] = 1
sparse_a[1, 2] = 2
sparse_b = lil_matrix((3, 3))
sparse_b[0, 0] = 3
sparse_b[1, 2] = 4
sparse_result = sparse_a.multiply(sparse_b) # 保持稀疏格式
print("稀疏矩阵逐元素乘:\n", sparse_result.toarray())
```
### 重要特性解释
1. **广播机制**：
当矩阵形状不完全相同但满足广播规则时，也能自动对齐计算：
```python
matrix = np.array([[1, 2], [3, 4]])
vector = np.array([10, 100])
# 广播：vector自动扩展为[[10,100],[10,100]]
print("广播乘法:\n", matrix * vector)
```
2. **性能优化**：
- 就地操作（`a *= b`）节省内存，原矩阵修改
- `np.multiply`相比普通运算符更灵活（支持dtype、where等参数）
3. **维度兼容性**：
- 处理任意维度数组，无需修改代码
```python
3d_array = np.ones((2, 3, 4))
print("三维数组乘法:\n", (3d_array * 3).shape) # 输出(2,3,4)
```
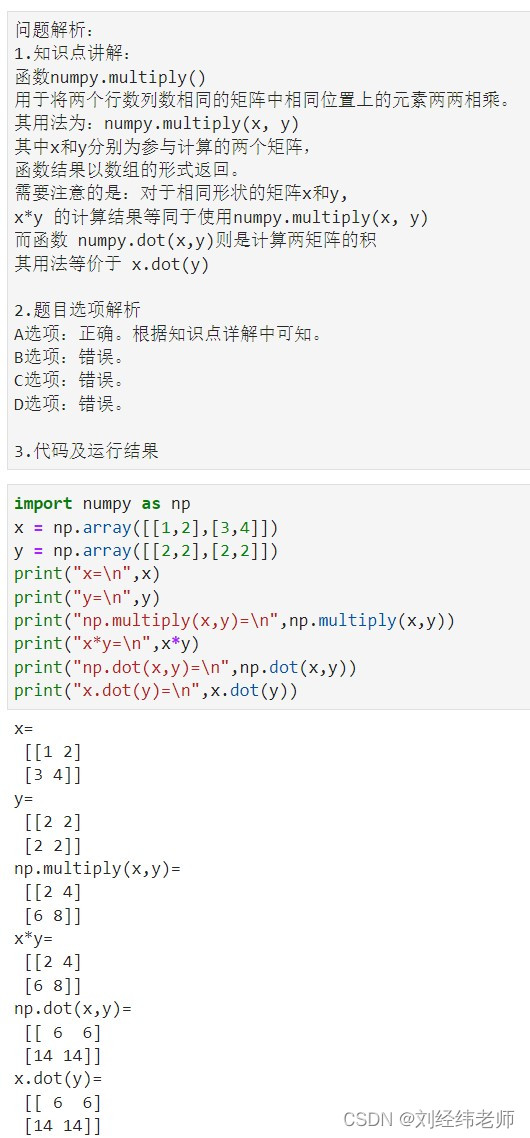
本文介绍了Python程序员如何使用numpy库实现矩阵乘法，并通过实例演示了np.multiply()函数在两个矩阵对应元素相乘中的应用。通过对比选项，解析了代码执行结果为A选项[[24][68]]的过程。
扫一扫
441
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
