强化学习导论 -章4 动态规划

强化学习中的动态规划方法

通过上一章的学习，我们已经了解了DP方法是如何进行价值函数的动态规划的

1. 动态规划概述

动态规划(Dynamic Programming, DP)是求解强化学习问题的基础方法之一。它要求我们有完整的环境模型(MDP模型)，包括状态转移概率 $P(s^{\prime }|s,a)$ 和奖励函数 $R(s,a,s^{\prime })$。

基本元素包括：

• 策略 $\pi (a|s)$
• 状态价值函数 $V_{\pi }(s)$
• 动作价值函数 $Q_{\pi }(s,a)$
• 贝尔曼方程

贝尔曼期望方程

状态价值函数的贝尔曼方程：

$V_{\pi }(s)={\sum }_a\pi (a|s){\sum }_{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma V_{\pi }(s^{\prime })]$

动作价值函数的贝尔曼方程：

$Q_{\pi }(s,a)={\sum }_{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma {\sum }_{a^{\prime }}\pi (a^{\prime }|s^{\prime })Q_{\pi }(s^{\prime },a^{\prime })]$

2. 策略评估

也称为预测问题，目标是计算某个策略 $\pi$ 的价值函数。显然，任何一个策略的评估函数是收到的回报期望，很显然，根据我们上一章的情况，对于一个动作策略不变的情况下，动作选择的概率不发生改变，对价值函数进行多次迭代会收敛到不动点，叫做：期望更新 此时是这个策略的状态价值函数
迭代更新公式：

$V_{k+1}(s)={\sum }_a\pi (a|s){\sum }_{s^{\prime }}{P}_{s{s}^{\prime }}^a[R_{s{s}^{\prime }}^a+\gamma V_k(s^{\prime })]$
通常，我们使用就地更新，直接用新值覆盖原值，可以收敛的更快

3. 策略改进及迭代

3.1 策略改进

很显然，基于之前的动作策略更新到的价值函数并不是最优解，例如我完全可以在任意一个状态s选择返回值最高的动作，显然最高的动作一定优于当前的加权的平均期望，所以一定是一个更好的策略

整体来说，如果在$\pi$策略下，使用新的策略的动作产生的动作价值，高于当前状态的在$\pi$的策略的状态价值，则认为是更好
$q_{\pi }(s,{\pi }^{\prime }(s))>=V_{\pi }(s)$

一个好的策略改进策略，定理保证了新策略的价值不会变差：

${\pi }^{\prime }(s)={\mathrm{argmax}}_a{\sum }_{s^{\prime }}{P}_{s{s}^{\prime }}^a[R_{s{s}^{\prime }}^a+\gamma V_{\pi }(s^{\prime })]$

3.2 策略迭代

策略迭代主要包含两个主要步骤：

1. 策略评估
2. 策略改进

这两个已经讲过了，基于刚刚已经更新了策略的情况下，那么对新的策略进行策略评估，从而继续完成优化的循环过程，直到所有的策略的动作都不在发生改变的时候

3.3 杰克租车问题

杰克租车的问题其实很复杂，原文中并没有详细说明杰克租车的问题的全部的规则和流程，实际的状态20*20，可以选择的动作也是20，是一个计算量很大的操作，实际计算机跑完这个过程的时间可能是按照分钟计算的，使用了time的模块，可以看到策略的评估和改进使用的时间分别如下
策略评估: 735.83 秒
策略改进: 89.69 秒

经过电脑多轮的策略迭代以后得到的策略图如下，颜色使用seaborn来生成热点图，

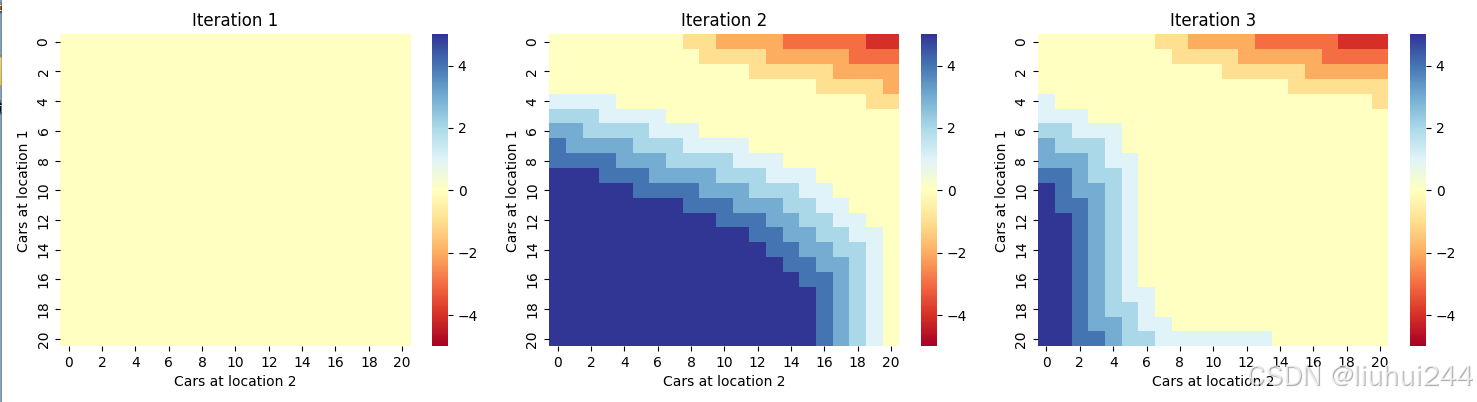
经过5轮迭代以后本地结果如图

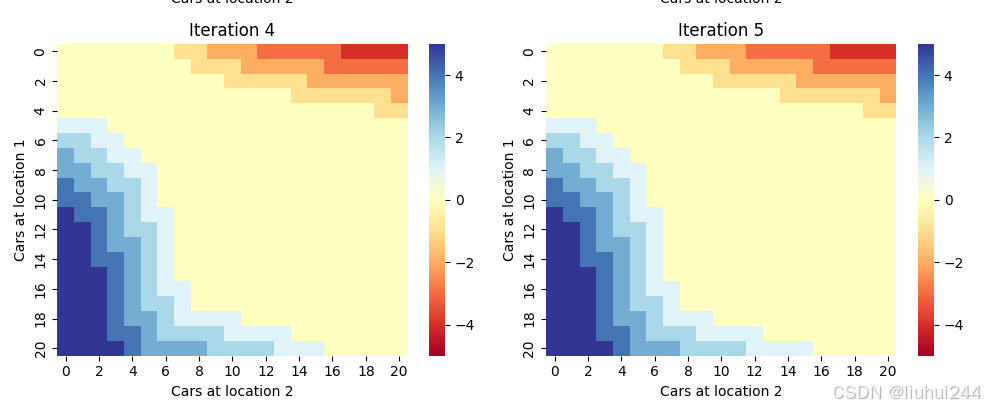
4. 价值迭代

价值迭代直接使用贝尔曼最优方程进行迭代，注意前面的策略评估是用的是期望值，这里直接使用了max来进行优化，如同前面使用映射压缩定理的证明，我们一样可以证明这是一个可以收敛到不动点的更新方式

$V_{k+1}(s)={\max }_a{\sum }_{s^{\prime }}{P}_{s{s}^{\prime }}^a[R_{s{s}^{\prime }}^a+\gamma V_k(s^{\prime })]$

当完成了价值迭代以后获取到的价值函数以后，那么最优策略可以通过如下的公式直接得出

${\pi }_{\ast }(s)={\mathrm{argmax}}_a{\sum }_{s^{\prime }}{P}_{s{s}^{\prime }}^a[R_{s{s}^{\prime }}^a+\gamma V_{\ast }(s^{\prime })]$

使用了价值迭代解决杰克租车的问题的整体耗时大约只有策略迭代的1/7，
总执行时间: 101.83 秒
初始化: 0.00 秒 (0.0%)
价值迭代: 92.13 秒 (90.5%)

5. 异步动态规划

为什么要有异步动态规划，如同我们前面介绍，所有的s都会在一次迭代的过程中被更新，但是一个强化问题可能超多的s状态，如果我们每个都更新将会损失很大的计算能力，我们可以任何一步都值更新一个函数值，只要保证序列序列无限长，那么可以认为一样会收敛到最后的不动点

异步动态规划的特点：

• 状态更新不需要严格的顺序
• 可以选择性地更新某些状态
• 其他状态的旧值仍然可用

异步动态规划的思想会在后面的章节里面大量使用到，用于从在线或者离线的经验中动态的学习和更新那些真实发生的过程和动作

6. 广义策略迭代(GPI)

广义策略迭代是策略评估和策略改进的概念框架，需要说明的是，总得来说，就是不停的使用更好的动作来使得当前价值更高，使用更好的价值来优化当前的动作，直到最后的收敛状态

• 评估当前策略(完全或部分)
• 根据当前价值改进策略
• 两个过程相互作用直至收敛

策略评估：
$V_{\pi }(s)\leftarrow {\mathbb{E}}_{\pi }[R_{t+1}+\gamma V_{\pi }(S_{t+1})|S_t=s]$

策略改进：
$\pi (s)\leftarrow {\mathrm{argmax}}_{a}Q(s,a)$

是否需要我进一步展开某个具体部分的内容，或者添加更多的数学公式和细节？