一、逻辑回归问题 Logistic Regression Problem
logistic regression多用于预测疾病。一个心脏病预测的例子:根据患者的年龄、血压等信息来预测患者是否会有心脏病。是否二字已向我们表名这是一个二分类问题,它的输出结果为{+1,-1}。
比较常用的情形是探索某疾病的危险因素,根据危险因素预测某疾病发生的概率。二元分类多数情况下,ideal target fuction f(x)>0.5,则判断为正类;若f(x)<0.5,判断为负类-1。
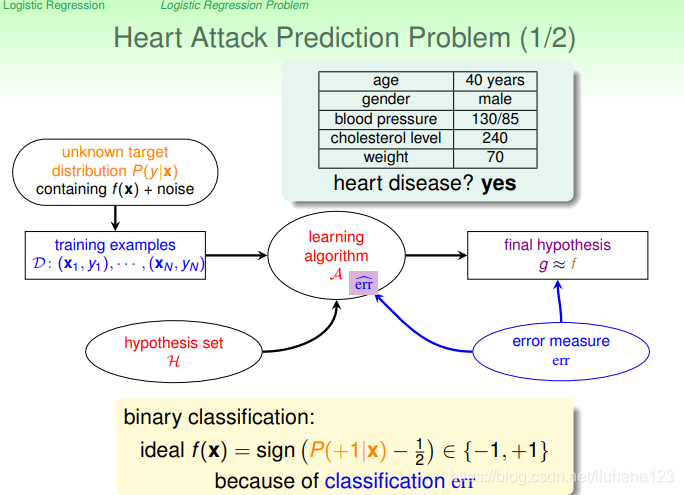
上面是我们想要的理想函数,f(x)会得到+1或-1的结果,作为是否有心脏病的结果。
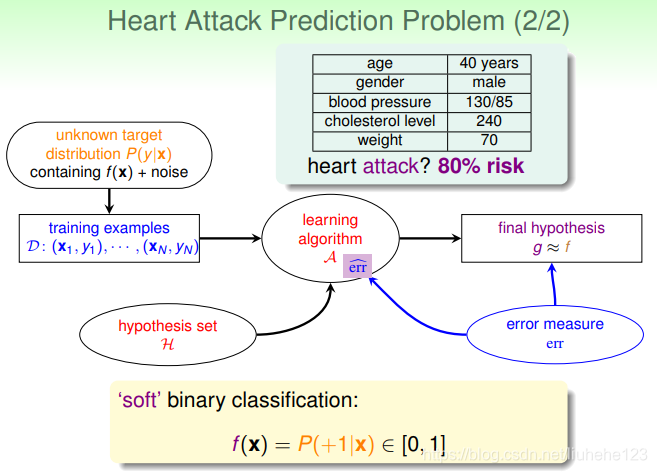
那么对于上面这种情况,我们想知道的不再是患者是否而是有多大几率是心脏病。几率则说明我们关心的值,及目标函数的值分布在0-1之间,其实我们更关心正类的概率,即患有心脏病的概率。这与我们平常所说的二分类问题不太一样,我们称这种问题为软(柔)性二分类问题(soft's binary classfication)。这个值越是接近1表示正类可能性越大,越接近0表示负类可能性越大。

![f(x) = P(+1|x) \epsilon [0,1]](https://i-blog.csdnimg.cn/blog_migrate/62e0f0298f10c84fc4b07983a030476b.png) 条件概率在已知(样本)x 的情况下得到+1的概率。我们想要的立项数据是分布在[0,1]之间的值,但是实际上我们在生活中只可能获得一个人是否患有心脏病,而对于他有多大概率则很难获得,即实际的数据只可能是0或者1。
条件概率在已知(样本)x 的情况下得到+1的概率。我们想要的立项数据是分布在[0,1]之间的值,但是实际上我们在生活中只可能获得一个人是否患有心脏病,而对于他有多大概率则很难获得,即实际的数据只可能是0或者1。

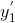 = 0.9 是极有可能患有心脏病的(正类-->1),
= 0.9 是极有可能患有心脏病的(正类-->1), 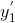 = 0.2则患心脏病风险相对很低(负类---> -1)。
= 0.2则患心脏病风险相对很低(负类---> -1)。
那么问题来了,如果我们理想的目标函数是:![f(x) = P(+1|x) \epsilon [0,1]](https://i-blog.csdnimg.cn/blog_migrate/62e0f0298f10c84fc4b07983a030476b.png) 的话,我们该如何找到一个好的Hypothesis来跟这个目标函数接近呢?即找到一个较好的h作为我们的
的话,我们该如何找到一个好的Hypothesis来跟这个目标函数接近呢?即找到一个较好的h作为我们的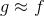 。
。
我们能够拿到心脏病患者的很多相关特征,有了这些特征我们可以进行加权处理,得到的结果s,称为risk score。
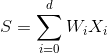 加权得到的结果加权和
加权得到的结果加权和,这样我们前进了一步,得到一个相关式子,但是我们想要的结果是将值限定在[0,1]之间。常用的一个方法就是使用sigmod function,记为
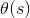 。于是我们的目标就是找到一个最好的hypothesis:
。于是我们的目标就是找到一个最好的hypothesis: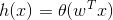 。
。

Sigmod Function的形式为,它满足
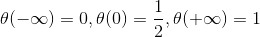 。这个函数是平滑的、单调的s型函数。那么对于我们的逻辑回归问题,hypothesis就是这样的形式:
。这个函数是平滑的、单调的s型函数。那么对于我们的逻辑回归问题,hypothesis就是这样的形式:
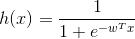
接下来我们的目标就是求出这个预测函数h(x), 使它逼近我们要的目标函数f(x)。
二、逻辑回归的错误衡量 Logistic Regression Error
线性分类可以通过0/1 err找到h(x), 线性回归可以通过square err找到自己的h(x),那逻辑回归给的误差err是啥呢?我们发现它的目标函数形式是![f(x) = P(+1|x) \epsilon [0,1]](https://i-blog.csdnimg.cn/blog_migrate/62e0f0298f10c84fc4b07983a030476b.png) 这样的,等式的右边是P 概率问题,我们要找的又是最接近f(x) 的hypothesis,这些条件我们可以应用极大似然来解决。极大似然就是找到一个与我们目标函数最相似(接近)的hypothesis, 这个hypothesis能和产生和目标函数一样的数据集D,包含y,那么这个hypothesis就是极大似然likelihood。
这样的,等式的右边是P 概率问题,我们要找的又是最接近f(x) 的hypothesis,这些条件我们可以应用极大似然来解决。极大似然就是找到一个与我们目标函数最相似(接近)的hypothesis, 这个hypothesis能和产生和目标函数一样的数据集D,包含y,那么这个hypothesis就是极大似然likelihood。

我们又称Sigmod function为logistic function: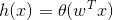 ,它满足一个性质:
,它满足一个性质:。
这里的性质用到:
关于某点中心对称: 两点横坐标的平均数等于对称中心的横坐标,两点纵坐标的平均数等于对称中心的纵坐标。
对于sigmod 函数对称中心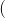
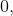

,
.
那应用上面的性质,我们说h(x)和f(x)非常的接近,则:

那么我们的似然性h:
![]()
性质:
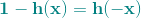
P(n)被写成灰色,是因为对于所有h来说,都是一样的,P(x)是先验概率,我们可以忽略它。我们得到的logistic h正比于,我们的目标就是让似然函数的乘积最大化,找到最接近的函数。
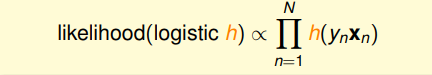

我们称为交叉熵误差(Cross-Entropy Error)。
需要解释的一点是,我们为什么在 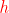 中要加入
中要加入 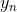 。 你看我们使用的数据集 D,如果他今天是个
。 你看我们使用的数据集 D,如果他今天是个(正类),我们就是
,如果他今天是
(负类),我们就是
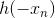 ,
, 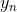 对应着+1、-1。这与我们上面的likelihood
对应着+1、-1。这与我们上面的likelihood正负对应。
我们已经知道: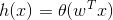
下面将权重w带入:
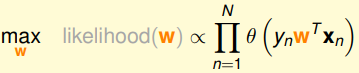
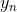 代表正负,
代表正负,可以放在
前面。
在求最大似然函数时,我们常常会用 In 函数将连乘问题转化连加问题,进而简化运算。
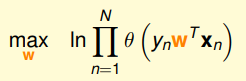
一下子就简单了好多,然后我们在将求最大值问题转化为求最小值问题,最小值问题更方便我们求解,添加一个符号就OK了,然后我们再求平均,引入1/N:
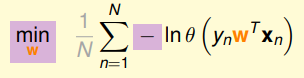
最后我们将我们的logistic function的表达式带入上式,我们的问题就有如下形式:
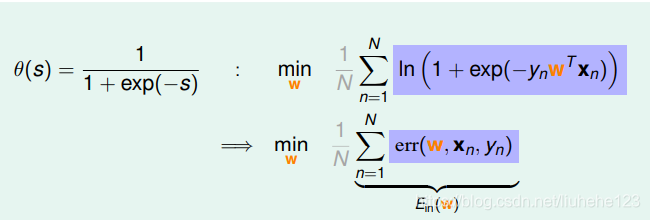
最终,我们也得到了logistic function的err function,即交叉熵误差:

三、逻辑回归错误的梯度衡量(Gradient of Logistic Regression Error)
我们已经推导了的表达式,那么接下来的任务就是找到合适的向量w,让
最小。
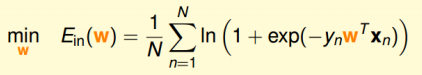
我们找到犯错的概率,让越小越好,这里的
是连续的、可微分的、二次可微的凸曲线(开口向上),我们先尝试一步登天求出
时的w,那么我们可以根据之前的线性回归的思路,先计算出
的梯度为零时的w,就是我们要找的最优解。
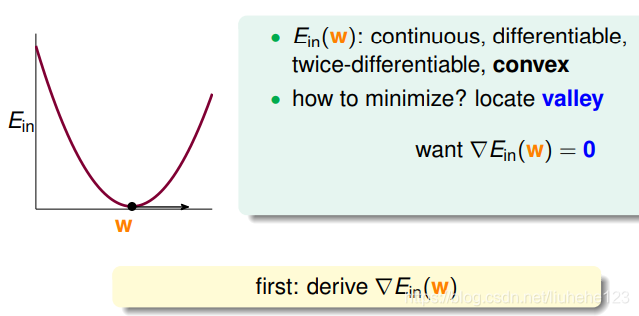
即我们对求关于w的微分:

得到的梯度表达式:
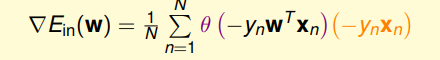 用一列高高的向量表示,而不是表达梯度里每一格是什么样子,
用一列高高的向量表示,而不是表达梯度里每一格是什么样子, 写成向量的形式。我们已经求得
微分后的表达式,接下来为了计算
最小值,我们就要求解
。
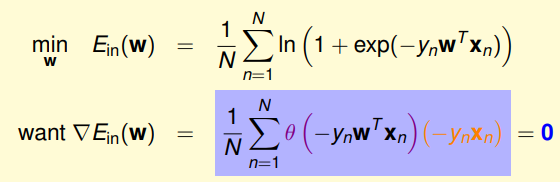
上面的式子,可以理解为是
的线性加权。这就要求
和
的线性加权和为0,其中一种情况就是先行可分的,如果
为0,就能保证
。
是sigmod 函数,根据该函数特性,只需
,即
,
说明对于所有的点,
与
都是同号的,这表示数据集D必须是全部线性可分的才能成立。
显然,这相当于已经提前预设条件了,假设所有点都是线性可分的,不过保证上面这种情况其实不太现实,总会有无法成立的情况,这就引出另一种情况了,非线性可分的情况,只能通过使加权和为0,来求解w。这种情况并不是封闭式解,这就与现行回归不同了,只能用迭代法进行求解了。

结果我们无法像线性回归那样一步登天求出w,我们可以想想有哪些算法是一步一步迭代求解的,我们之前看过的PLA算法,就是一步一步迭代进行的,每次对错误的点进行修正,不断更新w值。PLA的迭代优化过程:

我们首先找到错误,然后第二步进行修正,一步一步找到最后的w作为g。现在我们将两步合成一步。
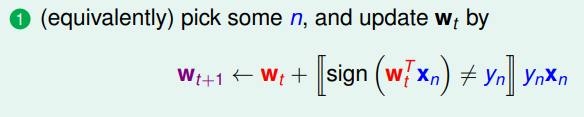
上面的意思是若这个点是错的就加上,是对的话前面就是加上0 *
,等于不做更新。

上面 代表我们每次更新的方向,
代表了每次更新的步长。参数
和终止条件决定了我们的迭代算法。
下面我们开始求解梯度下降算法。迭代算法让每次的w都有更新。

在这个过程,我们把曲线看成一个山谷,我们要求
最小,这就好比下山的过程,一直找到谷底就能得到
最小。下山有两个因素很重要,一个是下山的方向,如果走错方向就会事倍功半,还可能走不到谷底,另一个是下山的步长,如果不长总是太小,那么下山花费的时间就相当可观,如果太大,可能会使我们的下山过程看起来非常不稳定,甚至可能错过谷底。
分别代表了下山的单位方向和下山的步长。

我们要计算:。利用微分的思想,我们取一小段,即每次下山只前进一小步,即
很小,那么根据泰勒一阶展开式,可以得到:
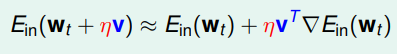
我们来详细写一下上面这个式子的计算过程:
首先我们要知道知识多元泰勒公式展开,有下面一些公式:
多元函数(n)在点处的泰勒展开式为:
把Taylor展开式写成矩阵的形式:
更多相关参考:多元泰勒展开式
首先我们的目标:
我们将 在
点展开,即取一小段,根据上面泰勒展开成矩阵的形式:
我们并没有写完全 所以才使用
我们进行迭代的目的就是让越来越小,即让
。
是标量,如果两个向量方向相反的话,那么他们的内积就最小(为负),也就是方向
如果和
方向相反的话,那么就能保证每次迭代都有
成立。那么我们另
与
方向相反,另外由于
又是单位向量,所有我们可以写出:
是单位向量,每次都沿着梯度的反方向走,也就是沿着导数不断变小的方向前进,这种方法称为梯度下降算法。
梯度:梯度的本意是一个向量(矢量),表示某一函数在该点处的方向导数沿着该方向取得最大值,即函数在该点处沿着该方向(此梯度的方向)变化最快,变化率最大(为该梯度的模)。 -----百度百科
迭代公式就可以写成:
我们已经看过了,现在来看看
的大小对迭代优化的影响:
如果太小的话,那么下降的速度就会很慢,
如果太大,那么使用泰勒展开的方法就不稳定了,我们使用泰勒是选取一小段,如果
步长太大,泰勒展开也就不准了,造成下降会很不稳定,甚至还会上升。所以要选一个合适的
,即在梯度较大的时候,
也会较大,在梯度较小的时候,
也很小,这样来看
正比于 梯度
。这样就保证能快速、稳定地得到最小值
。
。

我们用 来代替紫色的
于是有:
其中 :
我们上面的式子,当很大的时候,
就会很小,那么
正比于
,
也会很大,这样
就会增大步伐;当
很小的时候,
就会很大,那么
正比于
,
也会很小,这样
就会减小步伐。

这样,我们通过迭代可以求得最终的w。
注明:
文章参考:台湾大学林轩田机器学习基石课程学习笔记10 -- Logistic Regression





 本文深入探讨了逻辑回归在疾病预测中的应用,讲解了从硬性分类到软性分类的概念转变,介绍了Sigmoid函数及其在逻辑回归中的角色,以及如何通过极大似然法和梯度下降算法求解最优权重。
本文深入探讨了逻辑回归在疾病预测中的应用,讲解了从硬性分类到软性分类的概念转变,介绍了Sigmoid函数及其在逻辑回归中的角色,以及如何通过极大似然法和梯度下降算法求解最优权重。
















 1767
1767

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








