插入排序:
理念:在数组中,把一个数插入对应的位置,使得这个数组依然有序。
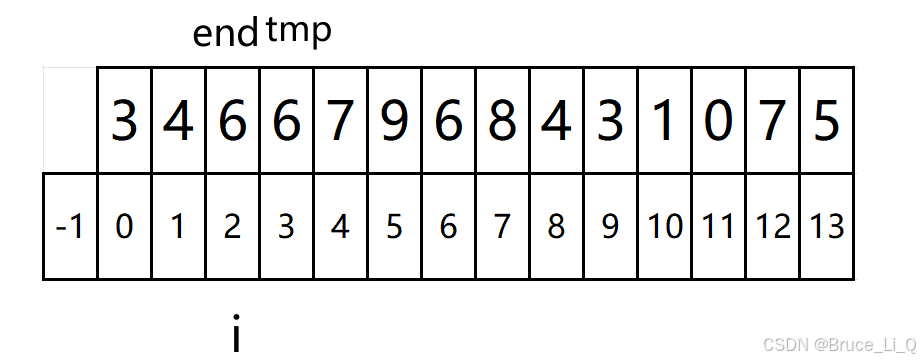
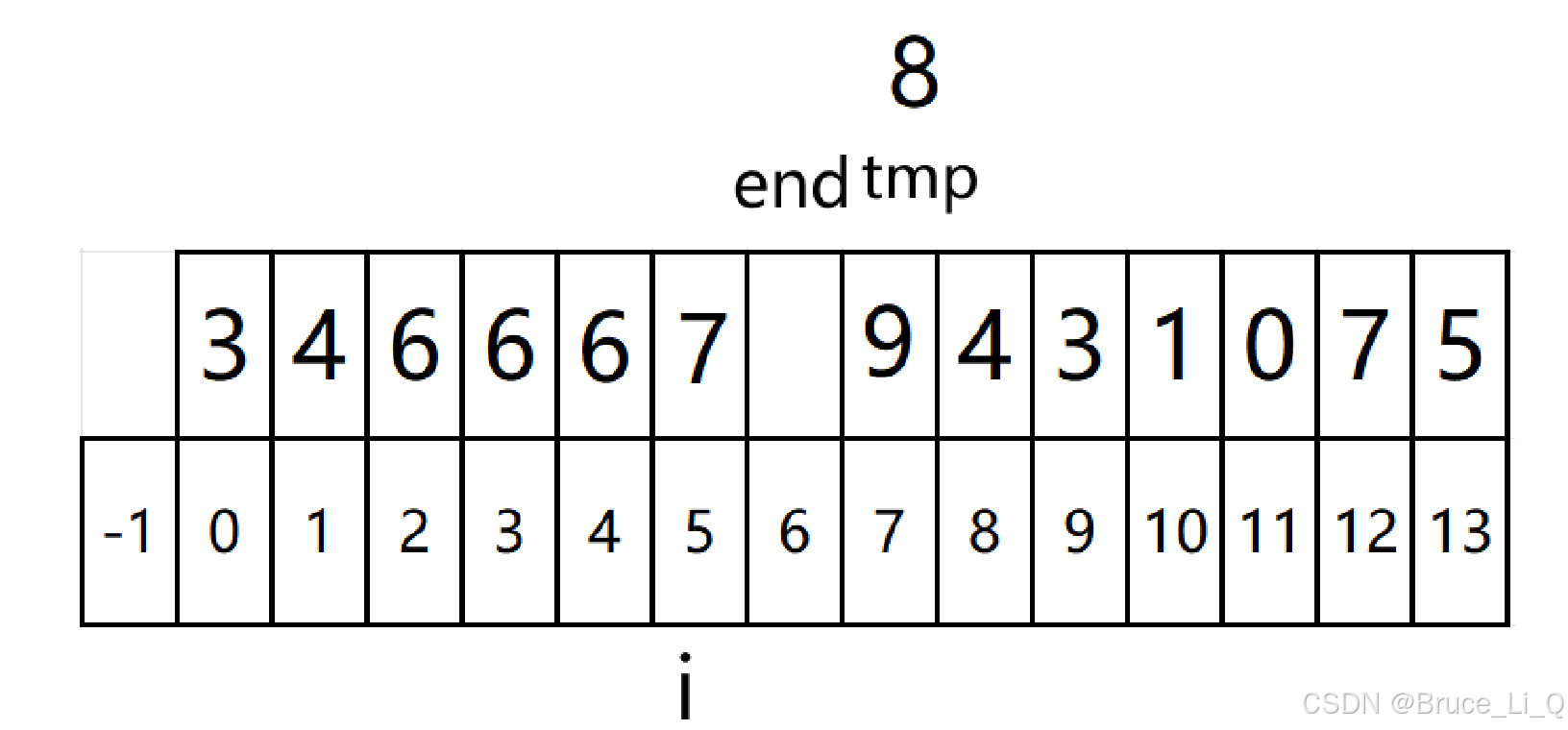
第一次进来 end =0;
判断 i 大于 tmp吗?不大于break , i+1= tmp ,不变
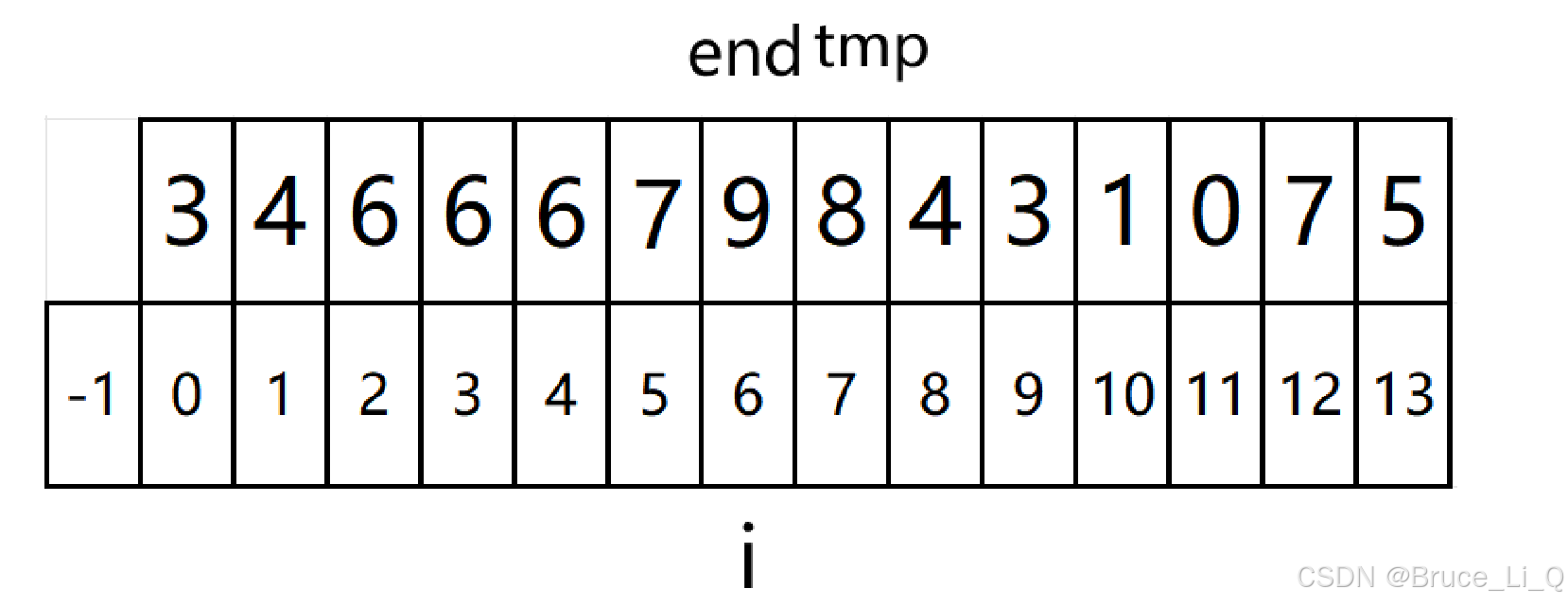
end++等于1 ,i 等于1,tmp=a[end+1]
i 大于 tmp , i + 1 赋值为 i , i 减减
再看 i 大于 tmp ,i + 1 = i , i减减
此时 i 已经不大于等于 0了,所以将 i+1 = tmp
随后 end++等于2,i = end,tmp =end+1(那个下标的元素).
由于没有大于的,所以end++等于3,i = end, tmp = end+1;
end=3也没有大的,我们直接来到 end=5
i 大于tmp,i + 1= i;i - -;
i 大于tmp i + 1 = i ; i - -;
i 不大于 tmp break,i + 1 = tmp;end++,i = end ,tmp = end+1;
i > tmp , i + 1 = i ; i - - ;
下面就是不大于将8 放入 i+1的位置,依次往后走就行。
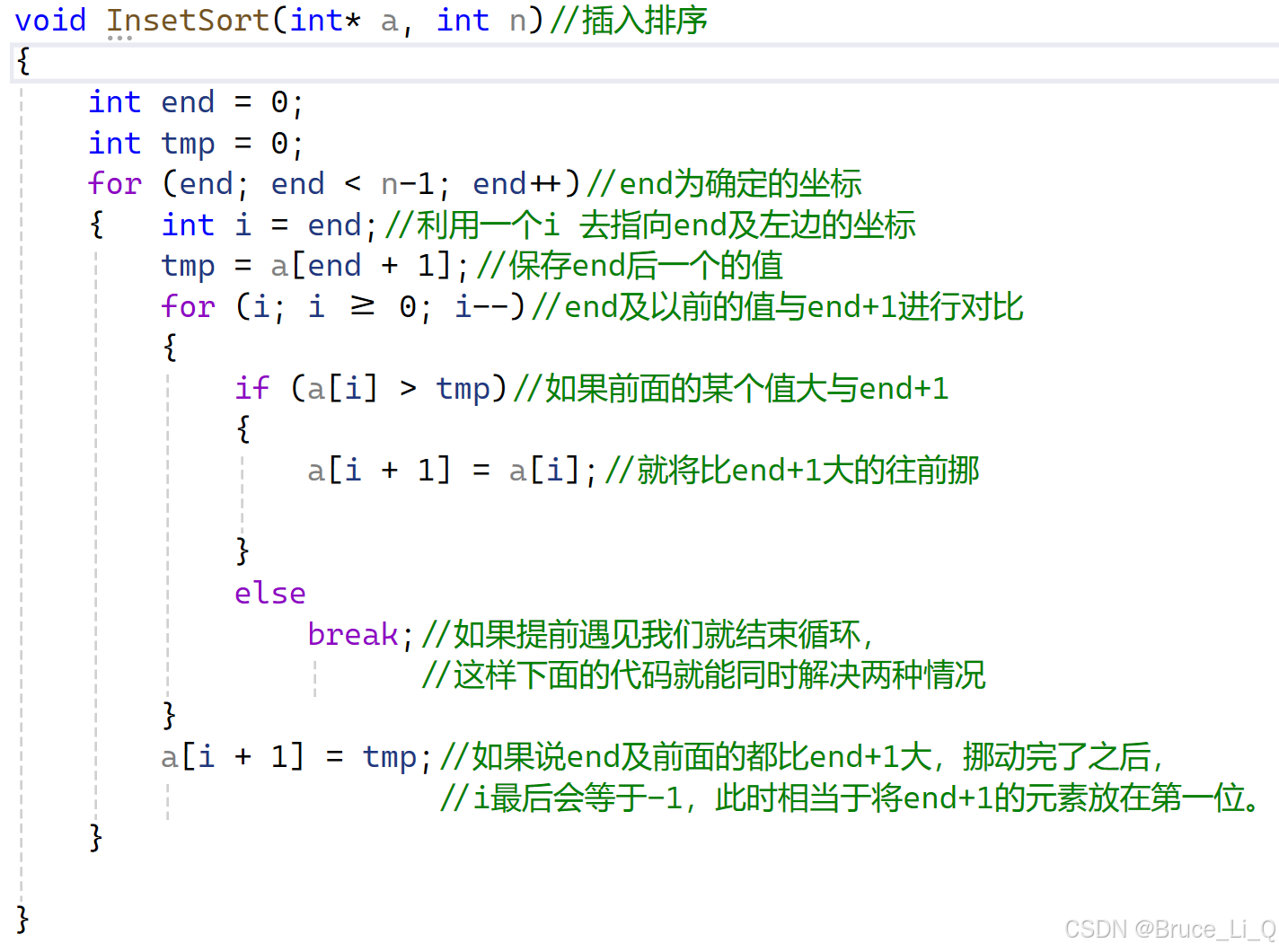
void InsetSort(int* a, int n)//插入排序 { int end = 0; int tmp = 0; for (end; end < n-1; end++)//end为确定的坐标 { int i = end;//利用一个i 去指向end及左边的坐标 tmp = a[end + 1];//保存end后一个的值 for (i; i >= 0; i--)//end及以前的值与end+1进行对比 { if (a[i] > tmp)//如果前面的某个值大与end+1 { a[i + 1] = a[i];//就将比end+1大的往前挪 } else break;//如果提前遇见我们就结束循环, //这样下面的代码就能同时解决两种情况 } a[i + 1] = tmp;//如果说end及前面的都比end+1大,挪动完了之后, //i最后会等于-1,此时相当于将end+1的元素放在第一位。 } }
希尔排序
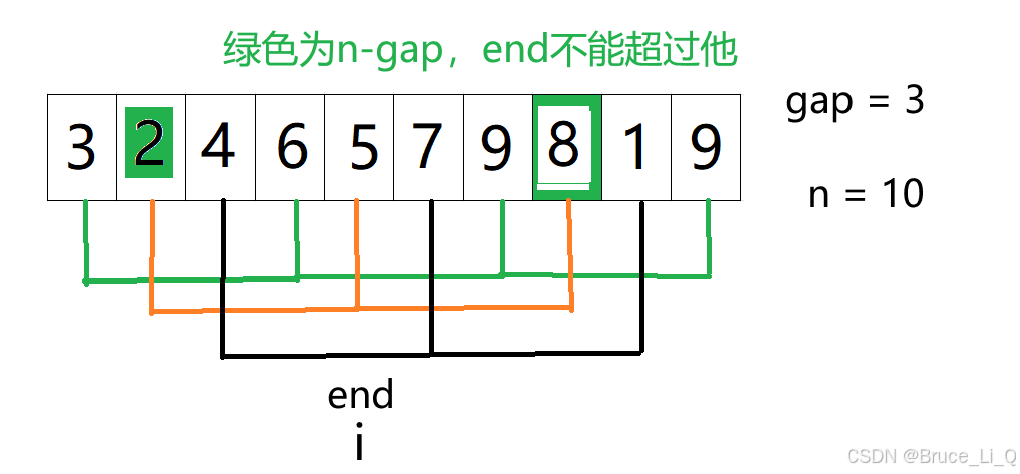
因为有gap的存在,使得当gap不为1的时候,能够预排序使得接近与有序,gap越大中间跳过的参数越多,也就越不准,当gap为1的时候就是插入排序了,此时,里面大概率已经很有序了。
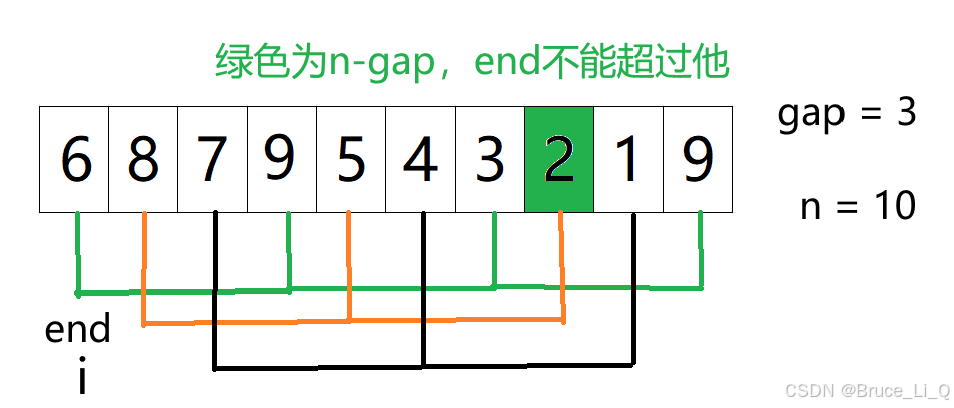
当end = 0, i = 0 ; 那么 i 是否大于 end + gap,大于,因为已经提前保存了 end +gap,
所以将 9,挪到 6的位置,随后i -= gap等于 -3,跳出循环,将 i +gap位置放入tmp(也就是end +gap),
end = 1,与上面一样
end = 2,也是一样
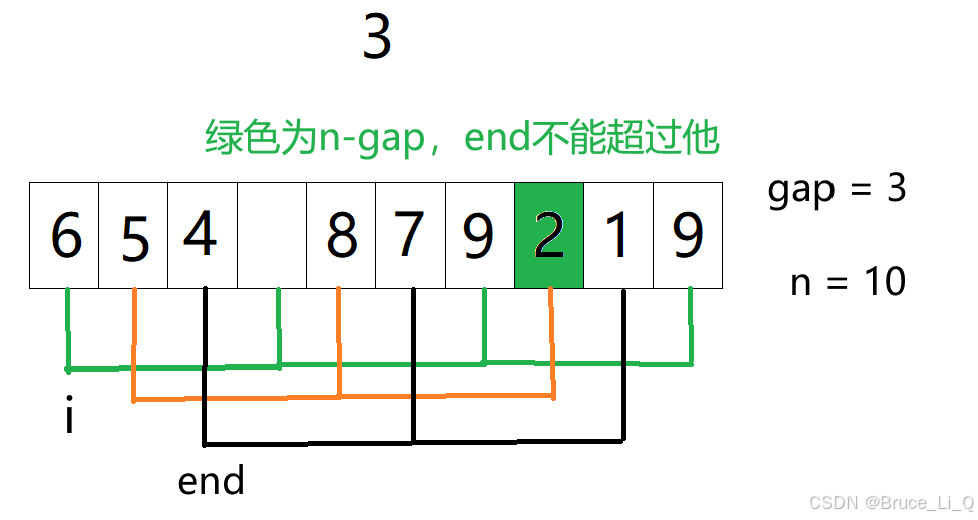
end = 3,这就不一样罗,首先保存 3 ,因为 9 大于 3,所以把 9 挪到 3的为位置随后
i -= gap等于0,
小差错,那个end 忘记调位置了,应该是在 空格位置
再比较 6 与 3 的大小,大于往前挪,此时i -= gap等于 -3跳出循环,可以将 3 放入 6的位置了。
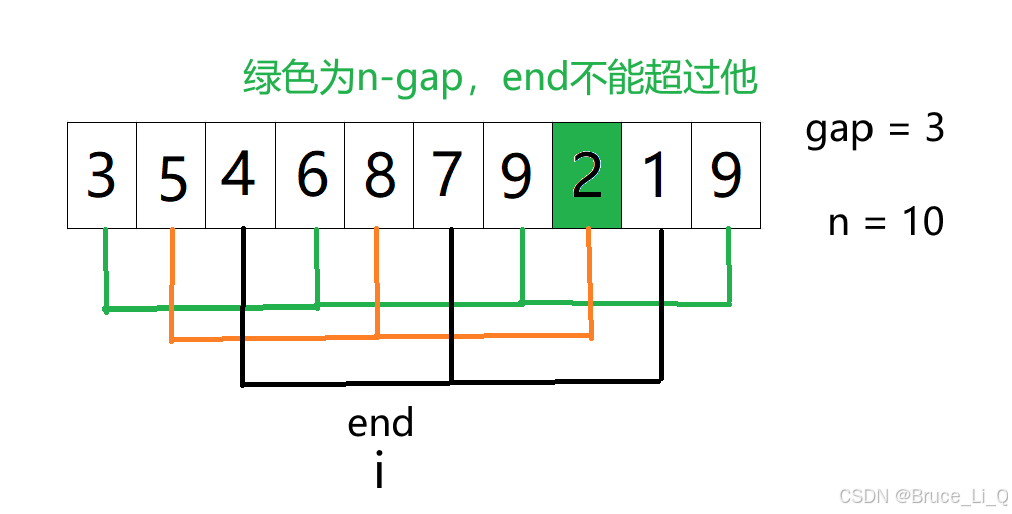
end = 4,8 和 5 都大于2,先将 8 挪到 2 的位置,再将 5 挪到 8 的位置,随后将 2 放入 5
完成后的顺序
顺序就是这么调整的,可参考图片对应代码食用。
void ShellSort(int* a, int n)//希尔排序 { int gap = n;//gap为确定下标的后gap个元素 for (gap; gap > 1; gap = gap / 2) { int end = 0;//确定下标的变量,每次gap刷新时下标再次来到0 for (end; end < n - gap; end++) //end < n - gap,当end走到n-gap-1时 //下方的tmp刚好等于最后一个元素,避免了越界 { int tmp = a[end + gap];//把确定下标的后gap个元素保存 int i = end;//拷贝一份end坐标 for (i; i >= 0; i -= gap)//把end以及前面end-gap的元素与end+gap的元素作比较 { if (a[i] > tmp)//如果大就往前挪动 { a[i + gap] = a[i]; } else break;//提前遇见终止 } a[i + gap] = tmp; } } }
堆排序
堆的结构
逻辑结构体是一个完全二叉树,物理结构体是数组
在一个数组里面,但是你得想象成是一个二叉树,根(下标为0)后面的两个元素是左子树(下标为1)和右子树(下标为2),到第四个(下标为3)和第五个(下标为4),就是第二个元素(下标为1)的左右子树,第六第七就是第三个元素(下标为2)的左右子树。
5,3就是4的左右子树,6,2就是5的左右子树,7,3就是3的左右子树。
下面为逻辑结构的样子。上面的是物理结构。
通过根找左右子树的的公式:
下标乘2再加一,为左子树下标
下标乘2再加二,右子树下标
通过左右子树找,根节点公式:
下标减一再除二,因为计算机的计算特性,比如,上图的 2(下标为3) 和 6 (下标为4),那么他们的根节点 5 (下标为1),不管你是 3 - 1除2,还是4 - 1除2,结果都为1.如果不一样那么说明根节点不一样。
向下调整算法:
目前是大堆,小堆的话只需要将红线中的符号变大于,运行逻辑在建堆那里。或者看注释
void Adjustdwon(int *a,int n,int root)//向下交换,特征是root 的左右子树都是满足大堆或者小堆的 { int parent = root;//parent 和 smallchild 均为下标 int smallchild = 0; while (parent <= (n-1-1)/2)//父节点不超过最后一个度不为0的节点 { //如果父节点的右子树在数组范围内,并且左子树小于右子树 if (parent * 2 + 2 < n && a[parent * 2 + 1] < a[parent * 2 + 2]) smallchild = parent * 2 + 2;//那么将孩子节点赋值为右子树 else smallchild = parent * 2 + 1;//如果说父节点的右子树不在范围,或者左子树大于右子树 //孩子节点赋值为左子树 //只要进入循环了,则表示父节点一定是有效的节点,一定有左右子树 if (a[parent] < a[smallchild])//如果父节点的元素小于孩子则交换 { int tmp = a[parent]; a[parent] = a[smallchild]; a[smallchild] = tmp; parent = smallchild;//将孩子节点赋值给父节点,这是为了能继续向下查找, //直到parent节点不在有效节点范围内,或者提前遇见了更大的数 } else//否则跳出循环,因为我们默认父节点的左右子树是满足大小堆的 break; } }
建堆
分为大堆和小堆:
大堆:根大于左右子树小堆:根小于左右子树
那么如何建呢?使得一个乱序的数组变成大小堆
以这幅图为列子,找到最后一个子树的根(绿色的3),让根与子树之间比较,小于就交换,然后去看绿色的7(这个去看的步骤为坐标减一),当我们的倒数第二层走完后,表示这一层都满足了根比子树小,只需要找到最后一个不为叶子的子树,然后判断交换,完了之后下标 减一,一直减到0下标,就是最后一次判断了。
一定要循环判断下去
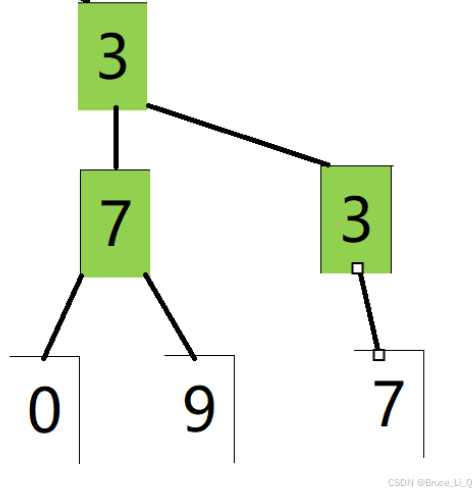
如果我们将,最上面的3改成10,
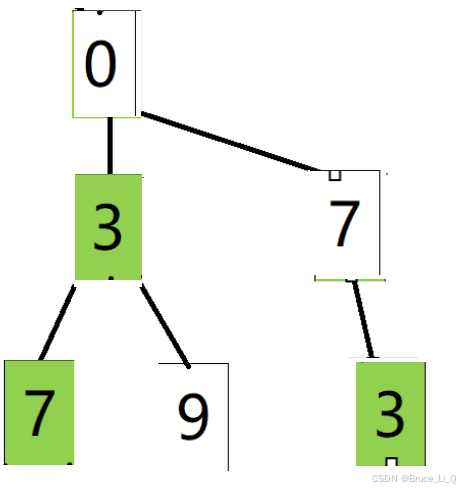
OK我们找到最后一个节点的根绿3,将他与7交换,
随后绿3- -,来到绿7,绿7与0交换,
减减,最上面是10,与0交换,10可不小7或者9,所以最好是能再次判断10与7 9的大小。
不直接将 绿3 改成10的原因就是有可能他是可以满足的。
调用上面的向下查找算法,从最后一个有效节点开始,就能实现建堆
排序
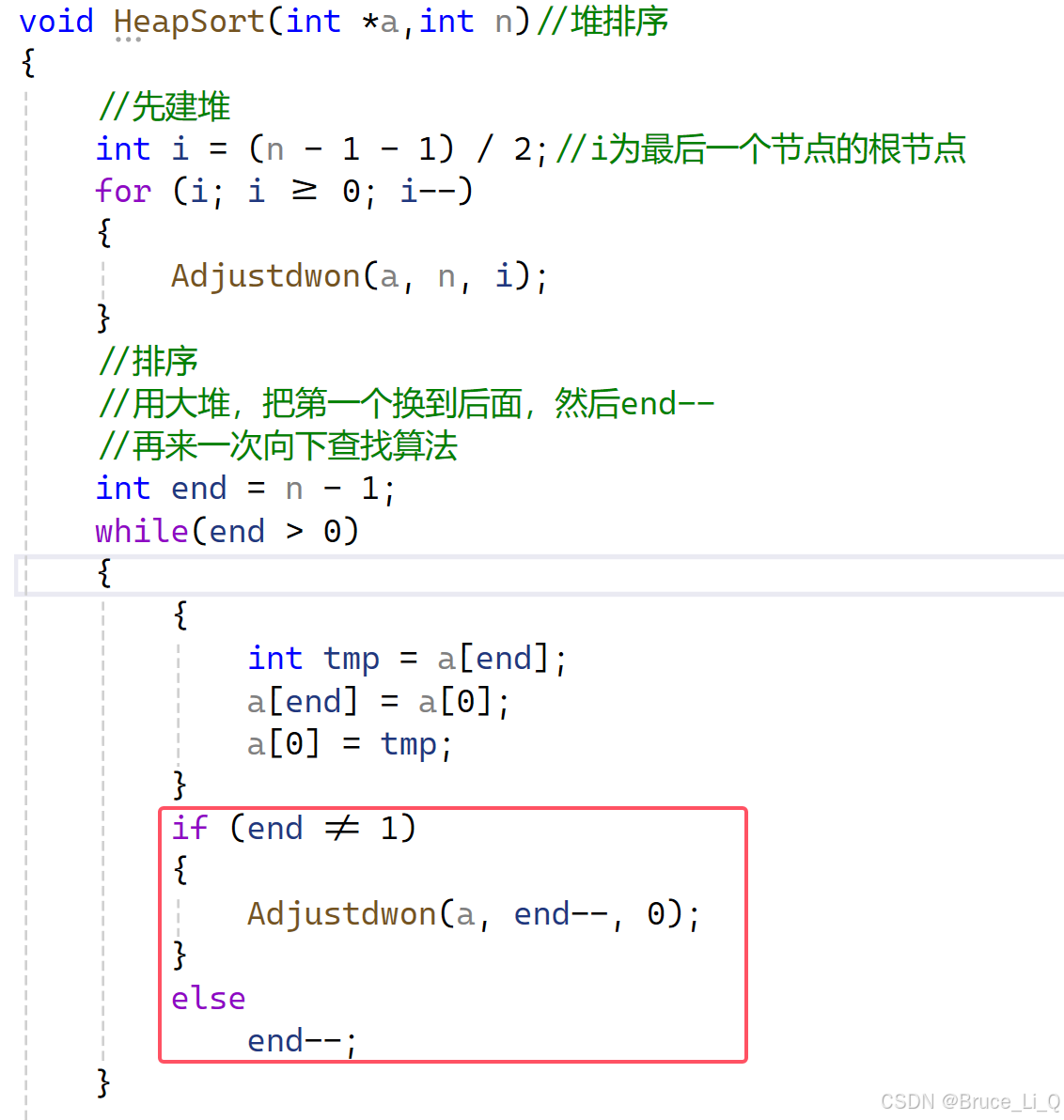
建完堆之后,将首尾交换,然后进入查找里面再找一个最大的数放在顶端,然后范围减一,继续交换,当范围等于1的时候,意味着还有两个数,这两个数交换之后就不用再进去找大数字放顶端了。
原因是:当范围是2的时候,还有三个数,一个根两个子节点,进来第一数就和第三个数交换,再 end 变成 2 之前,这三个数已经选出了最大数,所以进来交换,然后去看剩下的两个数谁大
,
end 还是 2 ,但是走到函数里面,右子树已经在范围内了,因为此时的右子树,是已经排好序的较大值。所以剩下 0,1比较,如果 “ 大 ” 会交换没有跳出。
此时,0 下标的数一定是大于 1 下标的数的。end - -等于1,while 循环条件满足,0 ,1交换,交换完之后所有数都有序了。不用再进去找最大数了。
那个If 语句也可以写成,如果等于1直接break,就行,不等与就进入
测试方法
双手请放在横向的数字键盘区,也就是字母区上面的数字区,然后快速的随便乱按,在那个数组里面。
然后用逗号将他们分开
最后运行检验结果,不放心的可以多试几次
直接选择排序
逻辑:两个变量,一个用来找最大值的坐标,一个用来找最小值的坐标,找出来之后,放在头和尾,随后头尾的坐标向中间靠拢。
有可能遇见起始坐标是最大值的情况,此时如果先将小的值放过去那么最大值就被覆盖了,即使是先换大值也有能遇见尾坐标是最小值,也会覆盖。两种情况选一种处理就行。
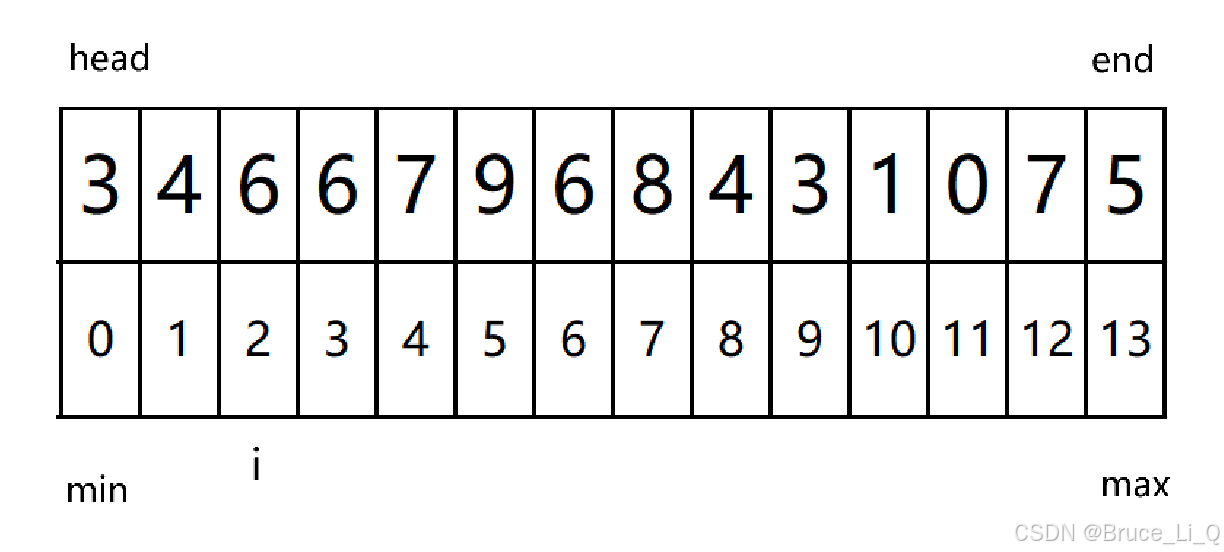
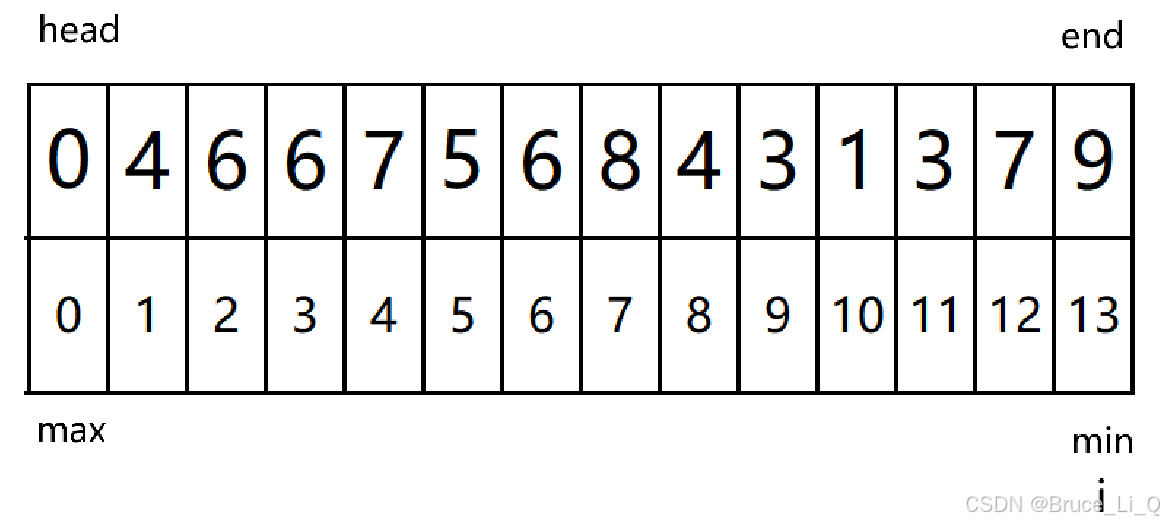
head 和end用来表示范围,min , max 最大最小值的下标,i 用来遍历
进入 i 的循环,i 小于 min 吗(i 下标和 min 下标的元素)?不小于,也不大于 max。
i++;
i 小于 min 吗?不小于同时也不大于
i++;
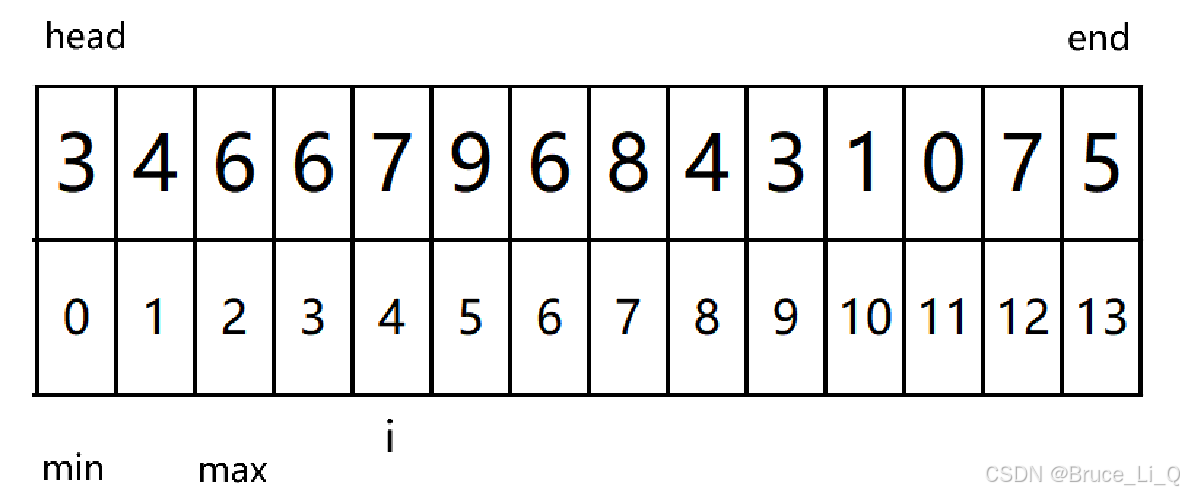
i 不小于 min 但是大于 max 所以 max = i(赋值的是下标);然后 i++;
i 不小于 min 也不大于max ,i++;
i 大于 max ,max = i; i++;
i 大于max , max = i ; i++;
max 已经是最大值了(就我们凭肉眼观察来说)。后面我就直接跳过使其 min 找到最小值。
之后 的 i++就没有操作了。来到交换,交换玩缩小范围
一般过程就是上述这样,接下来说一下特殊情况也就是这一段代码的由来
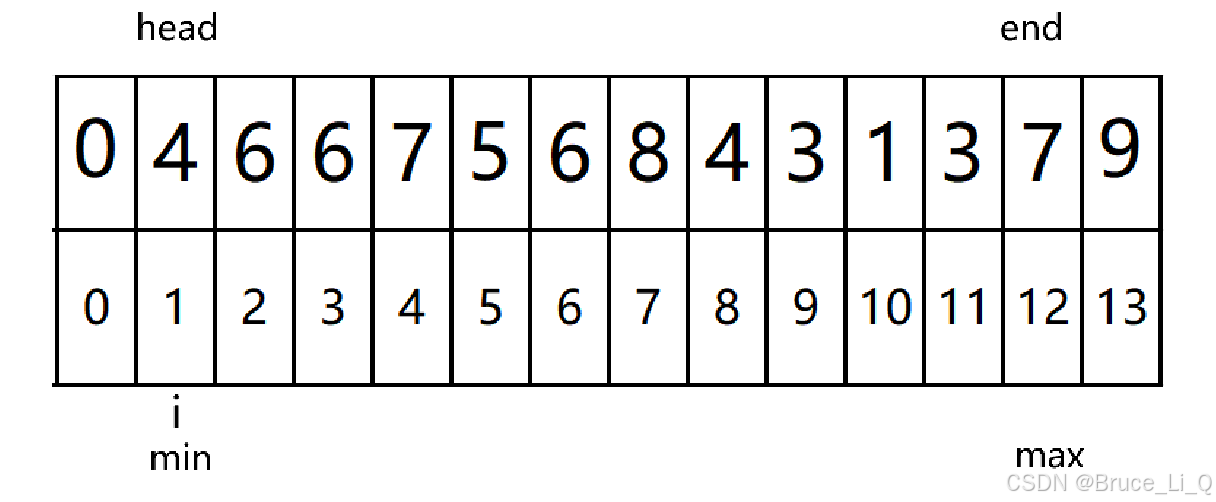
如果说确定 max 等于 head, end 等于 min ,ok 我们交换
head 与 min 先交换
然后, end与Max交换,就又交换回来了
所以当 head等于 Max 的时候,head 与 min 交换,此时min 指向的元素就是最大的那个 ,所以我们 max = min,就能解决。 min 不等于 end 也能解决
//直接选择排序 void SelectSort(int *a , int n) { int head = 0;//最小值放入的位置 int end = n - 1;//最大值放入的位置 while (head < end) { int i = head; int min = head; int max = end; while (i <=end) { if (a[i] < a[min])//i一直往后走,如果某个下标为i的元素小于第一个数,min = i; { min = i;//此时min 是当前最小值坐标 } //这两个 if 语句只会进来一个,说明当 i 既不小于最小的,又不大于最大的他就是中间值 //不用执行任何操作 if (a[i] > a[max])//如果 i 大于 max ,max 就是该坐标 { max = i; } i++;//可不能忘了写,要不然就死循环了 } {//最小值交换 int tmp = a[head]; a[head] = a[min]; a[min] = tmp; } //存在一个问题就是,head为最大值,交换完后,head 最小值 //此时max就是最小值,再交换的话,就将最小值移到最后面了 //head==max //end == min; if (head == max) max = min; {//最大值交换 int tmp = a[end]; a[end] = a[max]; a[max] = tmp; } {//缩小范围 head++; end--; } } }
快速排序
挖坑法
目标数组
函数主体
代码运行:
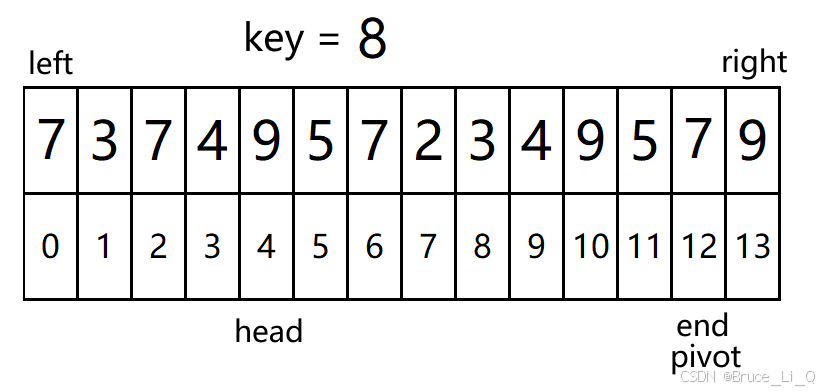
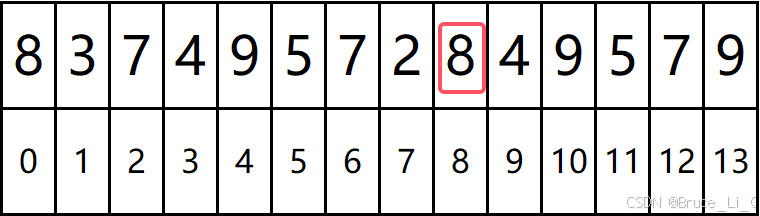
只讲一趟排序,将第一个 key 值放入正确的位置
对 挖坑函数调用,给他传首元素以及尾元素的地址
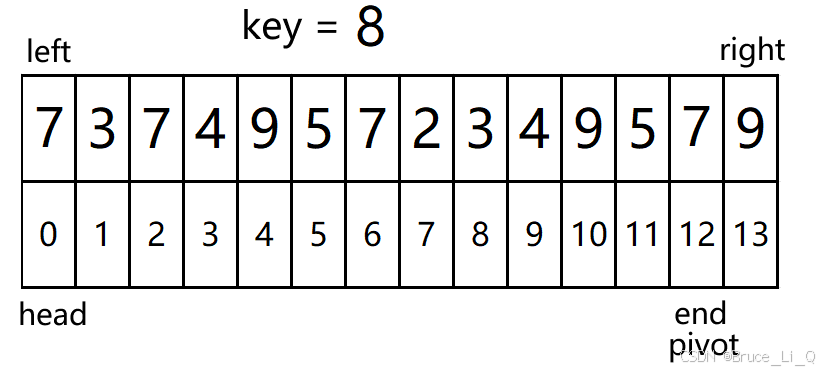
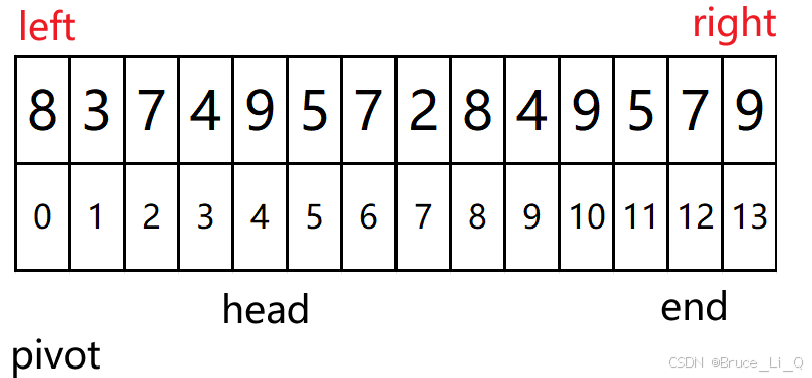
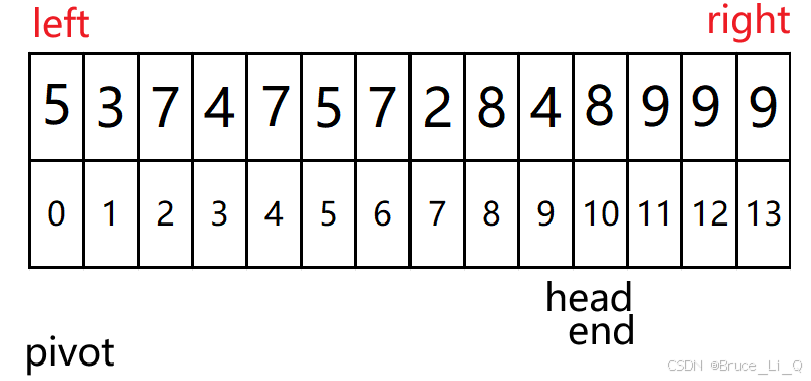
left = 0 ,right = 13
判断,left > = right ?,表达式为假,跳过
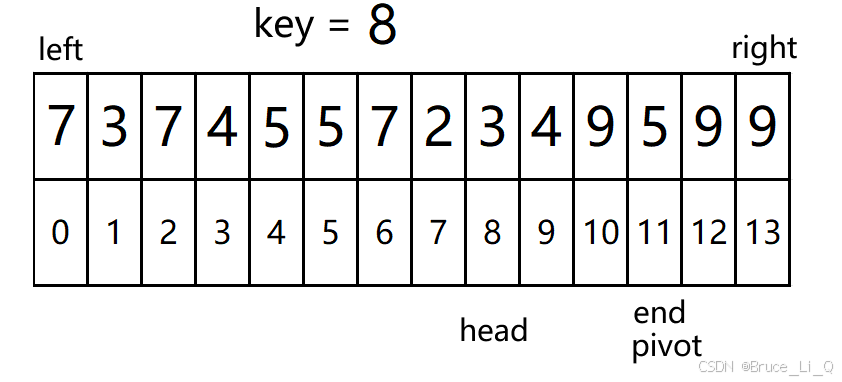
pivot(坑的坐标) = 0; key = 8 ; head = 0 ;end = 13;
进入外层循环 0(head) < 13(end),表达式为真
0 (head)< 13(end) && 9(a[end]) >= 8(key)?表达为真,end- -;
再次判断 0(head) < 12(end) && 7(a[end]) >= 8(key)?表达为假,循环结束;
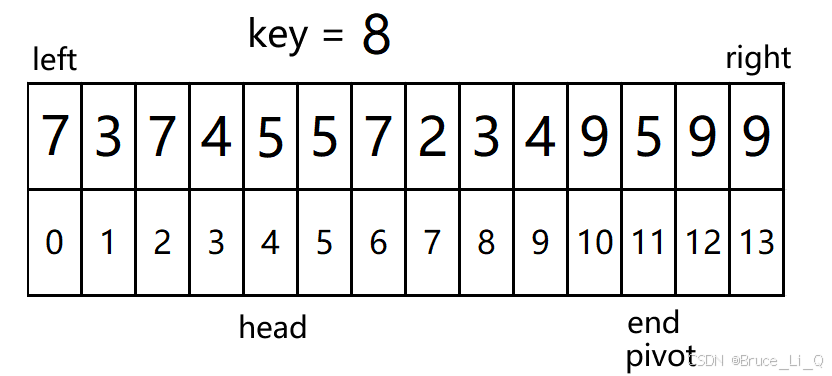
将 7 挪到 8的位置,然后pivot(坑)的坐标为 12
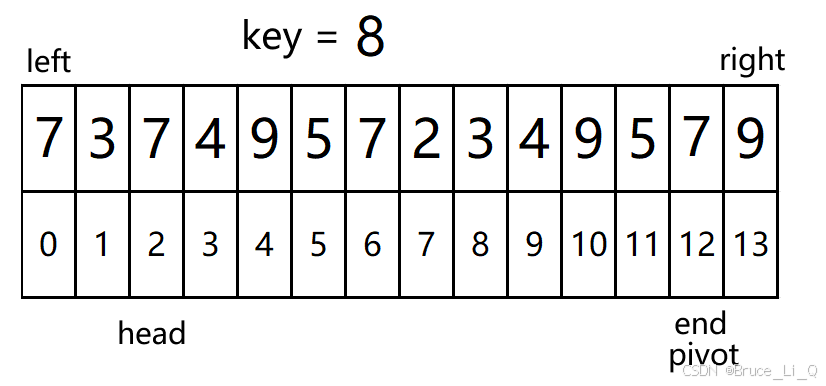
0(head) < 12(end) && 7(a[head]) <= 8(key)?表达式为真,head++;
再次判断 1(head) < 12(end) && 3(a[head]) <= 8(key) ,表达式为真 ,head++;
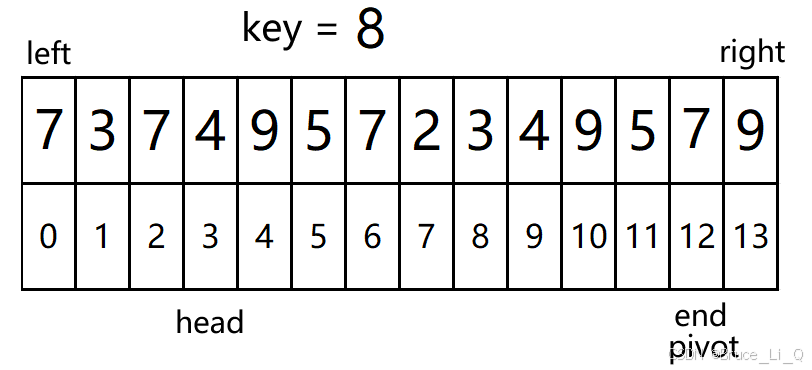
再次判断 2(head) < 12(end) && 7(a[head]) <= 8(key) ?表达式为真, head++
再次判断 3(head) < 12(end) && 4(a[head]) <= 8(key); 表达式为真head++
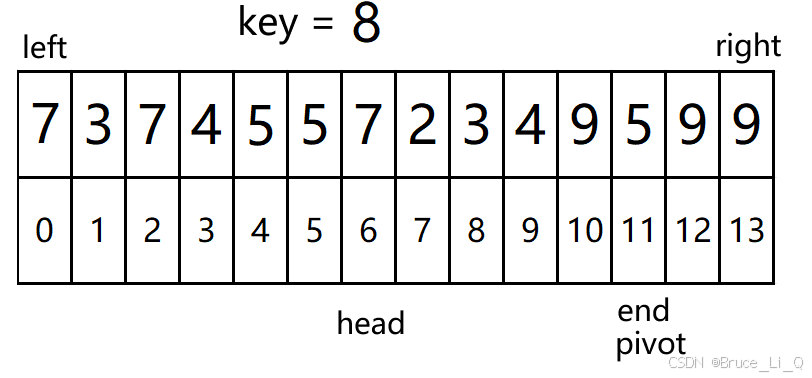
再次判断 4(head) < 12(end) && 9(a[head]) <= 8(key);?表达式为假 ,挪动 ,pivot = head;
head 判断结束,看一下 head与end 的关系,4 < 12表达式为真,进入
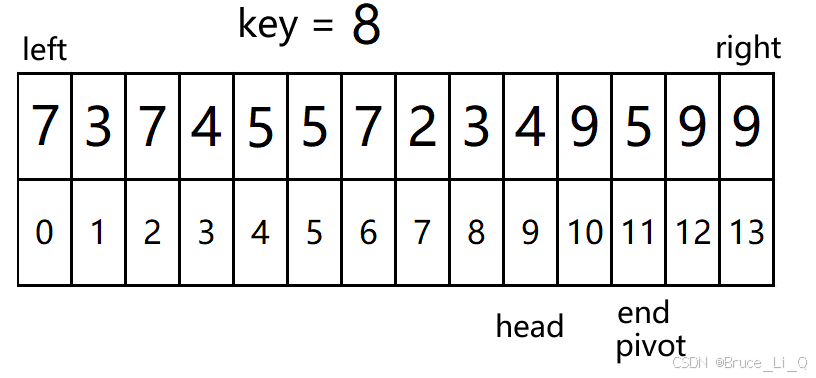
4(head) < 12(end) && 9(a[end]) > 8(key) ?表达式为真 ,end--;
再次判断, 4(head) < 11(end) && 5(a[end]) > 8(key) ? 表达式为假,循环跳出
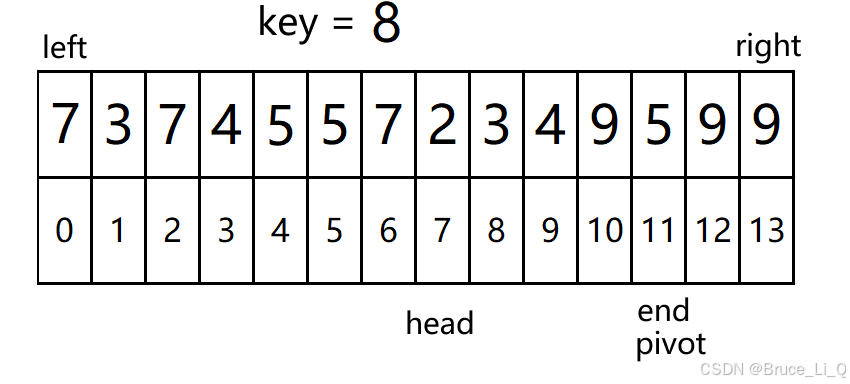
挪动 a[end ], pivot = end;
判断 4(head) < 11(end) && 5(a[head]) <= 8(key);?表达式为真,head++;
判断 5(head) < 11(end) && 5(a[head]) <= 8(key);?表达式为真,head++;
判断 6(head) < 11(end) && 7(a[head]) <= 8(key);?表达式为真,head++;
判断 7(head) < 11(end) && 2(a[head]) <= 8(key);?表达式为真,head++;
判断 8(head) < 11(end) && 3(a[head]) <= 8(key);?表达式为真,head++;
判断 9(head) < 11(end) && 4(a[head]) <= 8(key);?表达式为真,head++;
判断 10(head) < 11(end) && 9(a[head]) <= 8(key);?表达式为假,执行
判断
,10(head) < 11(end)为真进入
判断
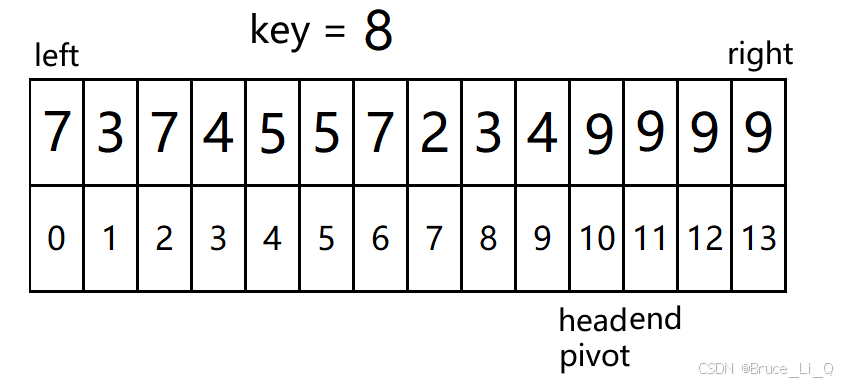
10(head) < 11(end) && 9(a[end]) >= 8(key) , 表达式为真,end --;
11(head) < 11(end) && 9(a[end]) >= 8(key) , 表达式为为假,执行
由于 pivto 和 end 在一个位置,不用交换了。
11(head) < 11(end) && 9(a[end]) >= 8(key) , 表达式为为假,执行
由于 pivto 和 head 在一个位置,不用交换了。
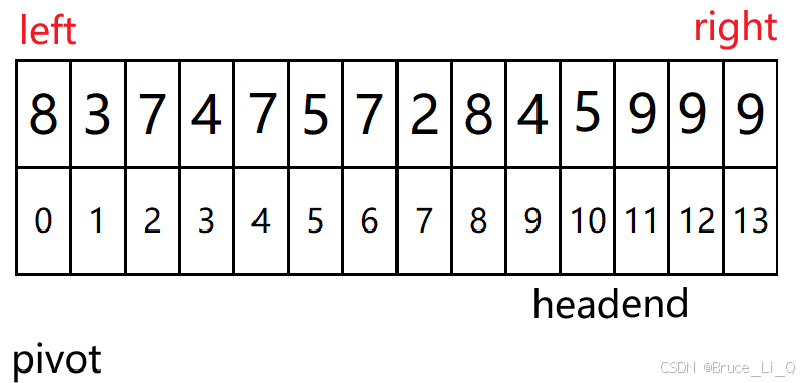
最后
,表达式为假,外层循环也结束了。
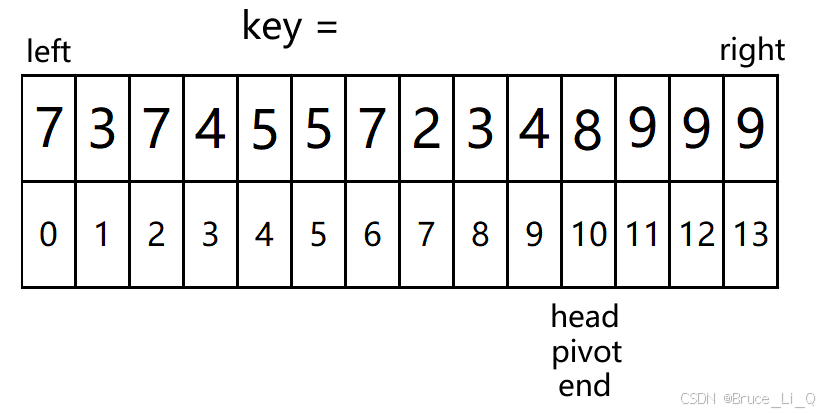
将 关键字放在坑的位置
这样关键字的坐标都是小于等于关键字的值,右边的都是大于等于关键字的。所以如果关键字相同数太多,第一趟结束后,你去观察,如果你不知道哪一个是具体的关键,可能会发现主观上的不对,其实是对的。
然后说一下区域的划分
左区域为
右区域为
依次递归下去,直到
这俩相等就开始返回
交换法
逻辑:head找大,end 找小,找到了之后,head 和 end 交换。
当他俩相等时,将 pivot 对应的值放入 他俩当中的任意一个坐标当中。
代码运行
这一把咱们加个8 进去
直接跳过一些步骤,直到左为大,右为小停止
然后对他俩交换
交换完之后,head < end 再次右找小,左找大,代码的顺序是,先右后左
然后交换
然后end--与head ,end = head ,他们俩再交换不变,相遇跳出循环
随后 pivot 与 head再交换
然后和挖坑法一样再分区域递归下去
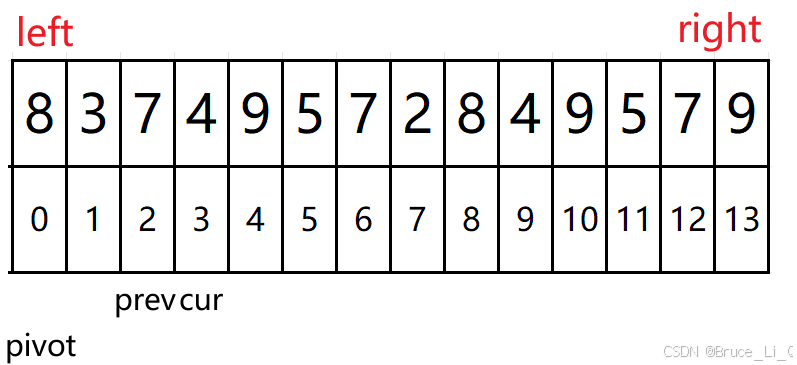
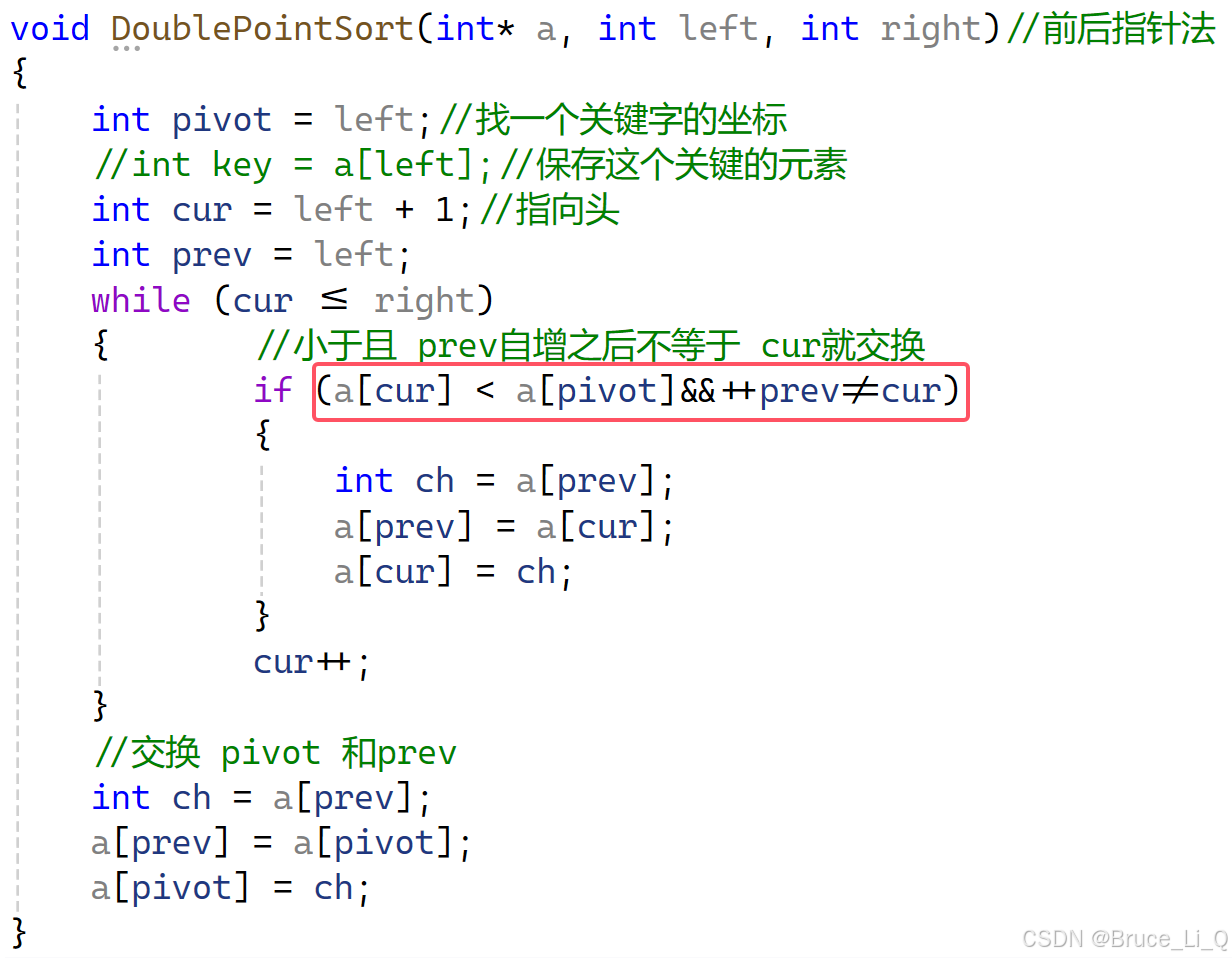
双指针法

判断,a[cur] 3 < a[pivot ] 8 && ++prev != cur ,前一个表达式满足,可 ++prev 等于 cur,不进入判断语句,然后
上来又判断
进来之后再次判断
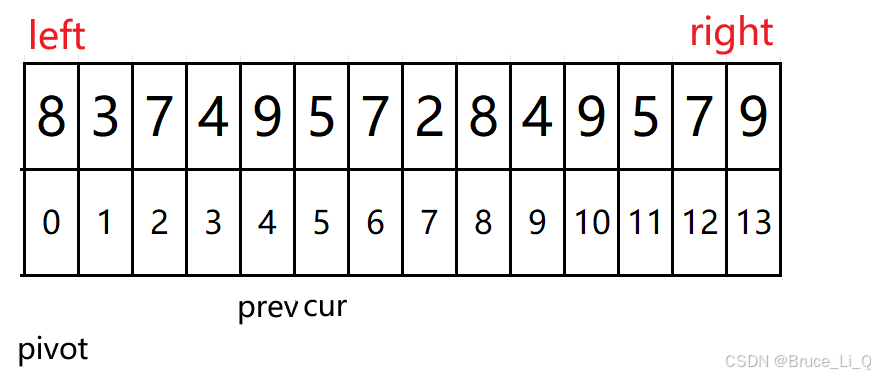
7 < 8 && 2 != 2 表达式为假,cur++
cur <= right 为真
4 < 8 && 3 != 3表达式为假 cur++;
cur < = right 为真
到了这里 ,先判断的 9 < 8为假此时后面的 ++ prev则不会执行了。
所以只会 cur++;
cur <= right
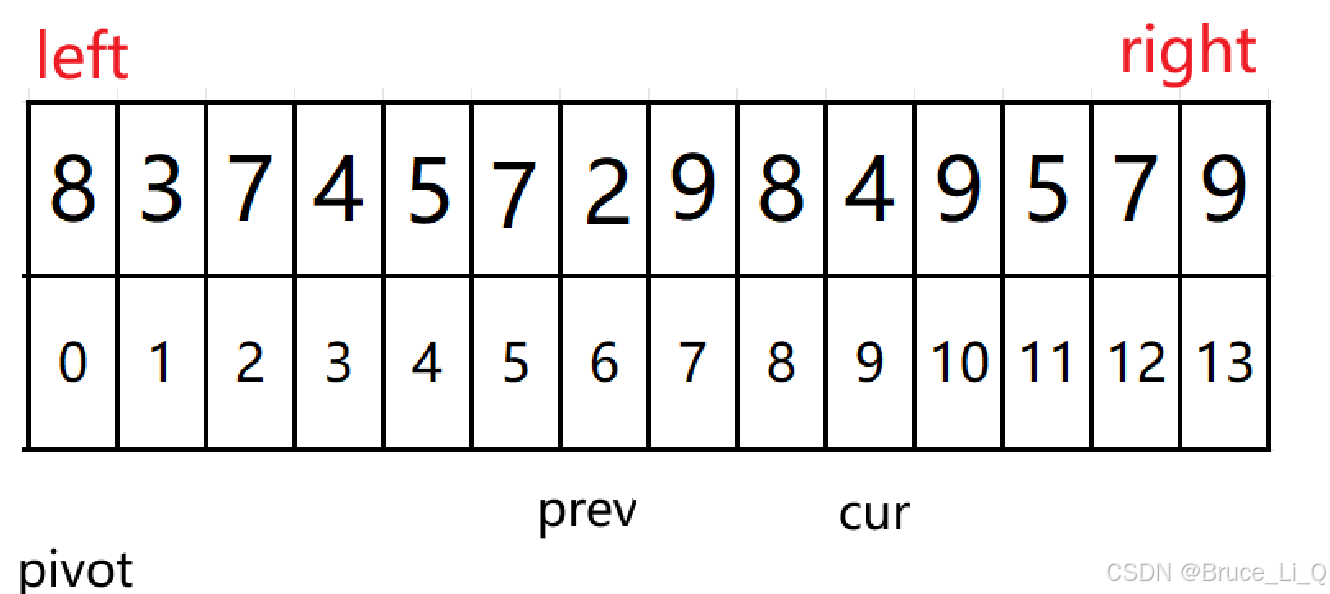
5 < 8 && 4 != 5 表达式位置呢执行
,交换prev 和cur 里面的值
然后 cur ++;
操作为 prev++;
交换
交换完之后 cur ++;
cur <= right
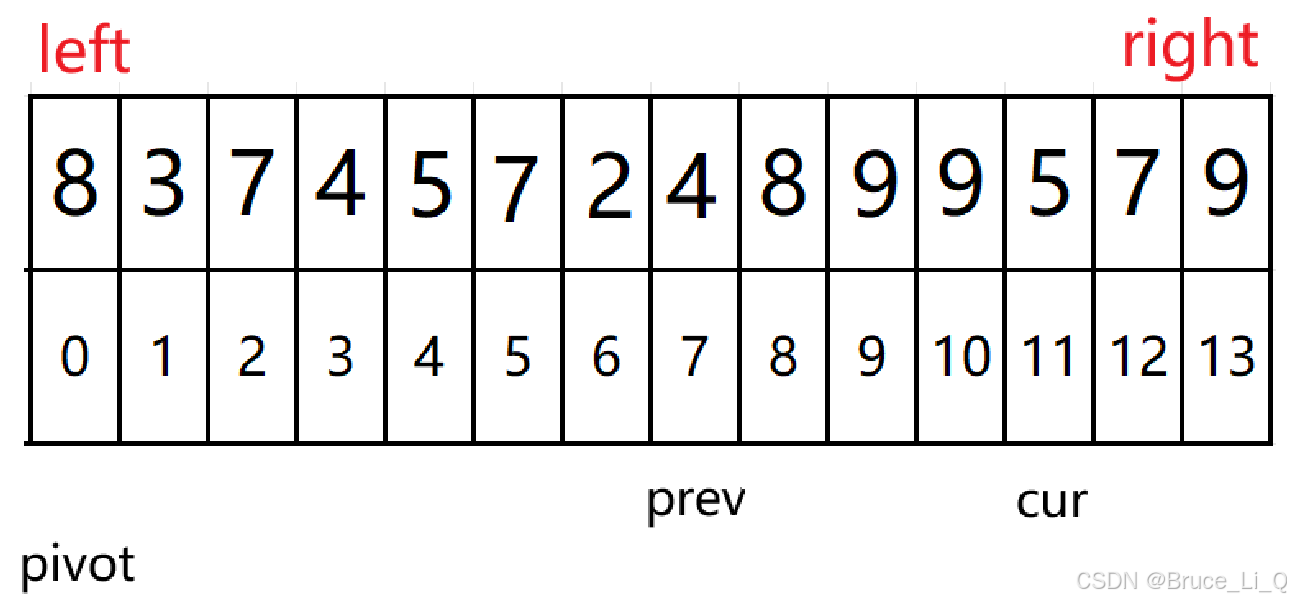
7 < 8 && 5 != 6,表达式为真 ,9 与 7交换 ,随后 cur ++;
cur <= right
2 < 8 && 6 != 7,表达式为真,9 与 2 交换 cur++;
cur <= right
8 < 8 表达式为假 cur ++
cur <= right
4 < 8 && 6 != 9 ,交换 cur ++;
cur <= right
9 < 8 表达式为假 cur ++;
cur <= right
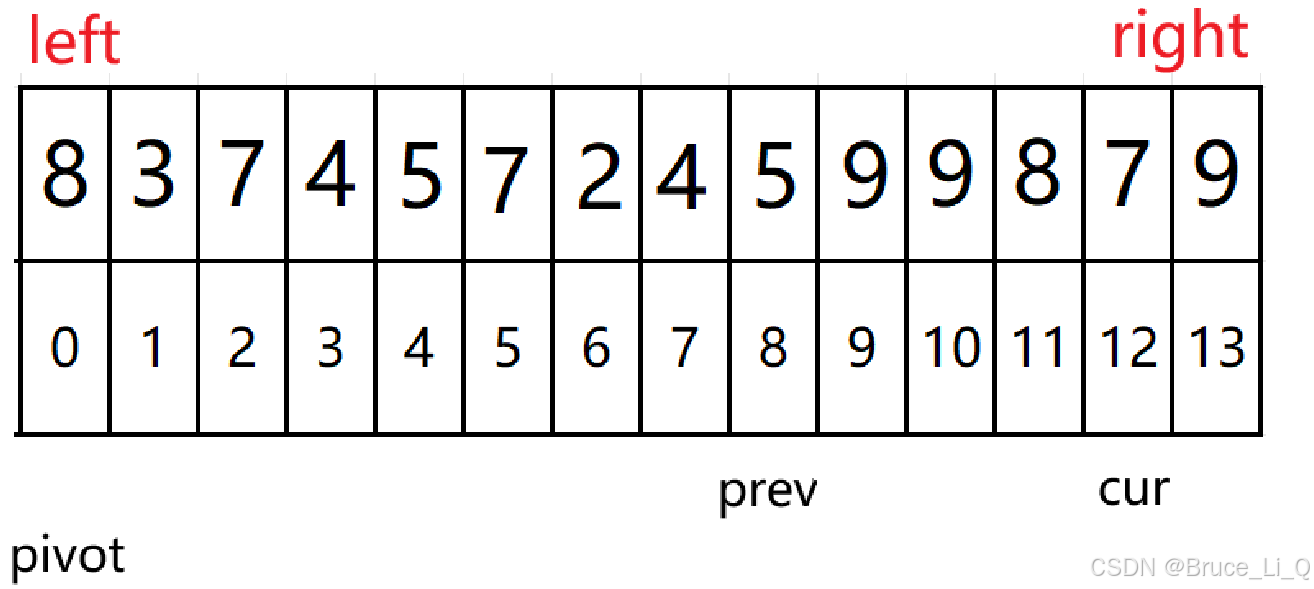
5 < 8 && 8 != 11 ,表达式为真 ,交换 cur++;
cur <= right
7 < 8 && 9 != 12 ,交换 cur++;
cur <= right
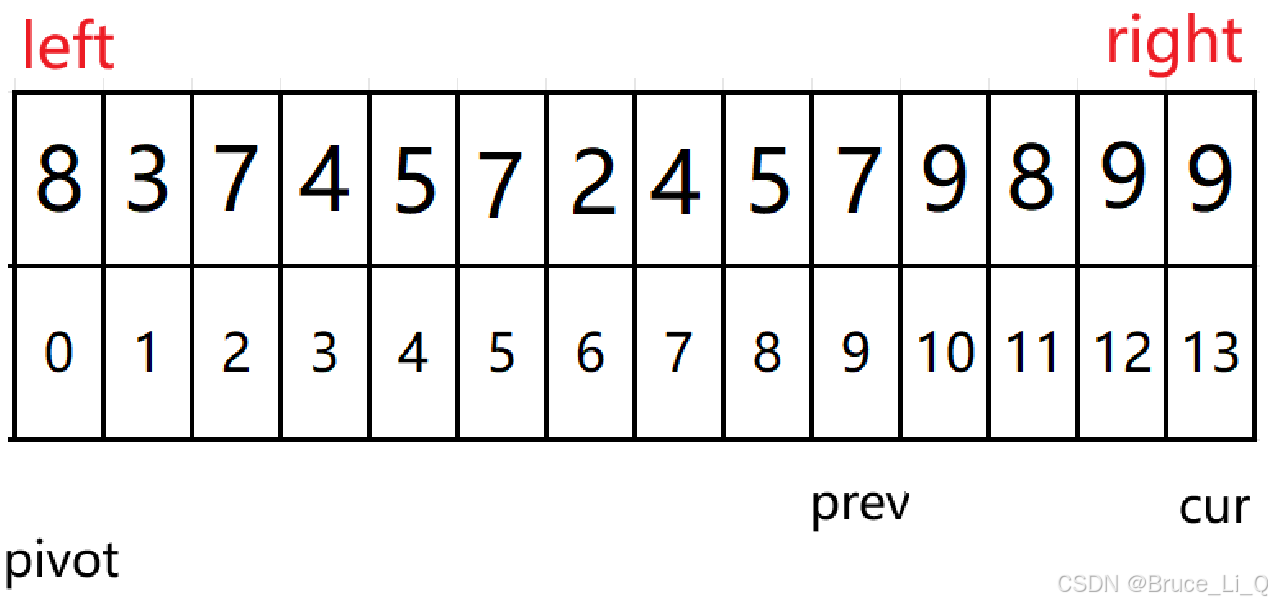
9 < 8 表达式为假 cur ++;
cur <= right
9 < 8 表达式为假,cur++;
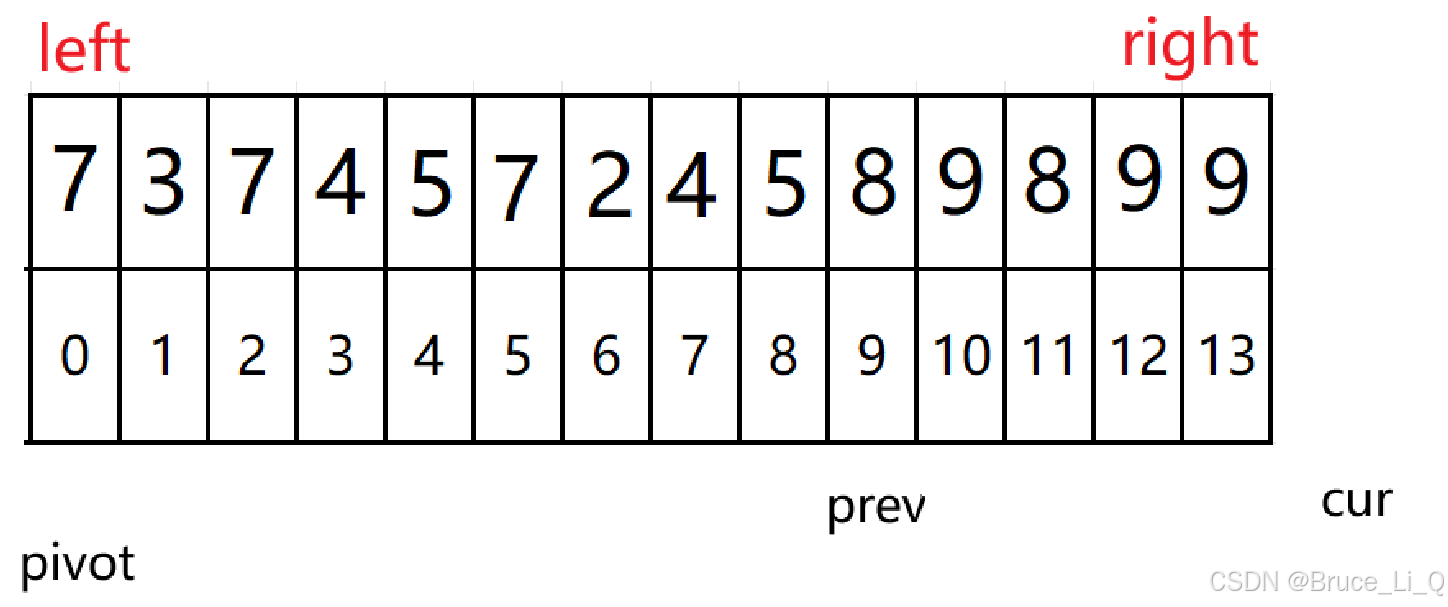
cur <= right 表达式为假 外层循环结束,交换 prev 与 关键值pivot
交换
最后来个逻辑推理:
根据这一段代码可知,每次发生交换的情况是 cur 指向的值小于 pivot 指向的值,cur 往前交换,能使得 prev 之前的值都小于 pivot 。最后 prev与pivot 交换,就能使得,关键值(pivot )之前的值都是小于,不用担心,最后 pivot 与 prev ,交换时,prev大于关键字 ,因为那个值经过 cur 的验证的,小于 prev才会指向








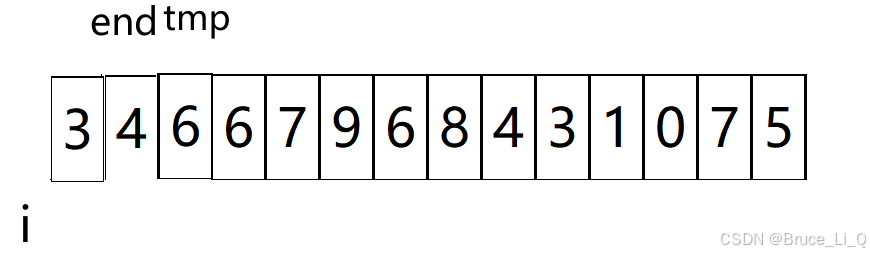
























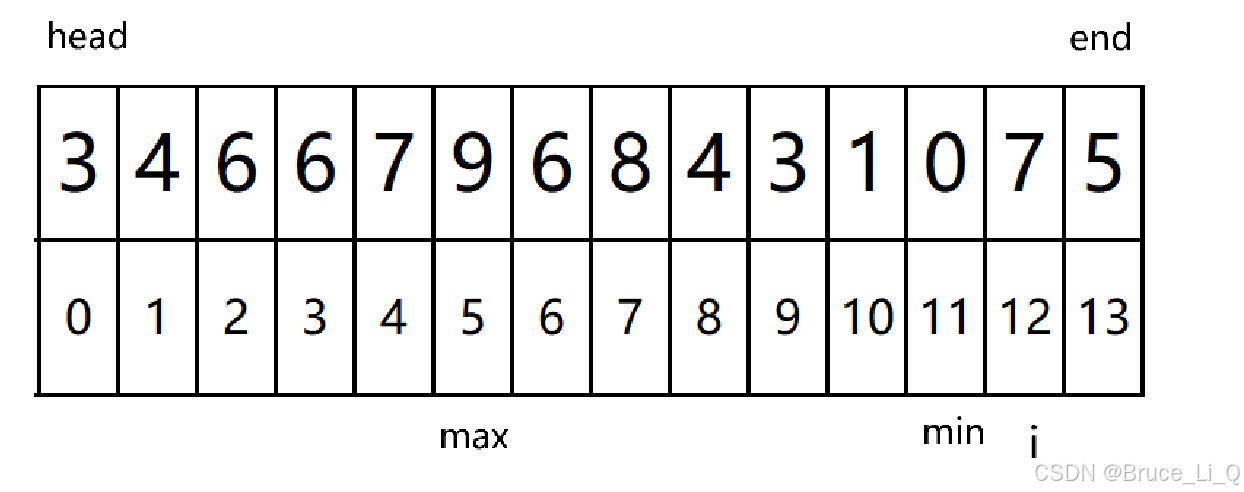




























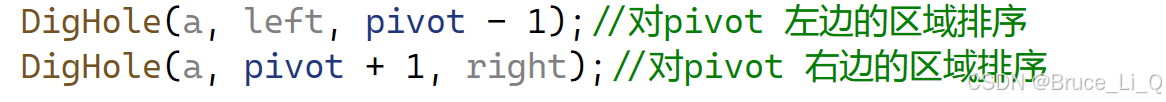








































 5157
5157

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








