背景
前提知识(线性代数、概率论)
- 特征值与特征向量
- 对称矩阵对角化、非负定矩阵
- 正交矩阵,矩阵的转置与逆
- 正交变换
- 协方差矩阵
引言
问题提出
在实际生活中,我们往往会用很多指标(又称属性、特征、因素)来尽可能的描述我们所要分析的对象,在数学上我们利用向量X=(x1,x2,...,xn)X=(x_1,x_2,...,x_n)X=(x1,x2,...,xn)来表示拥有nnn个特征的对象。假设我们要预测明天某只股票是跌还是涨,我们收集了这只股票一年内每一天的指标,比如当天开盘价、收盘价、前N天最高价、前N天最低价、前N天平均价、当天全国平均气温、当天全国人口出生数、当天全国人口死亡数等等一系列指标(为了说明问题,我这里举了一些影响不大的因素)。当然我们知道在这些指标中对研究对象的影响是不一样的,比如像平均气温、人口出生数与死亡数对股票涨跌影响弱,像开盘价与收盘价对股票涨跌影响强。所以我们能不能通过某种算法使得用更少的指标去描述股票涨跌这个现象,以便我们能够便利地进行数据处理?
问题解决
上文我们了解了每一个指标对股票涨跌的影响是不一样的,那我们能不能通过剔除掉那些对股票影响弱的指标来达到缩减指标的目的呢?答案是不能的,因为在我们收集指标时往往有些指标是比较“鸡肋”的:留下的话,感觉对股票涨跌影响不是很大,徒增数据处理压力;剔除掉,想想对股票的涨跌还是有一定的影响的。主成分分析正是很好的解决了这种问题,我们可以通过对这些指标一些线性组合yi=a1ix1+a2ix2+...+anixn,其中i=1,2,...,my_i=a_{1i}x_1+a_{2i}x_2+...+a_{ni}x_n,其中i=1,2,...,myi=a1ix1+a2ix2+...+anixn,其中i=1,2,...,m,m≤nm\leq nm≤n。最终我们就可以通过向量Y=(y1,y2,...,ym)Y=(y_1,y_2,...,y_m)Y=(y1,y2,...,ym)这m个指标来描述股票涨跌这个现象,所以我们可知,主成分分析主要解决的问题就是求解组合后的指标yiy_iyi,也就是求解(a1i,a2i,...,ani)这些组合系数,其中i=1,2,...,m(a_{1i},a_{2i},...,a_{ni})这些组合系数,其中i=1,2,...,m(a1i,a2i,...,ani)这些组合系数,其中i=1,2,...,m。
特征空间
在引言中我们知道股票涨跌现象可以用向量X=(x1,x2,...,xn)X=(x_1,x_2,...,x_n)X=(x1,x2,...,xn)来描述,这也构成了我们研究对象的特征空间。比如,下图就是一个n=2的特征空间:
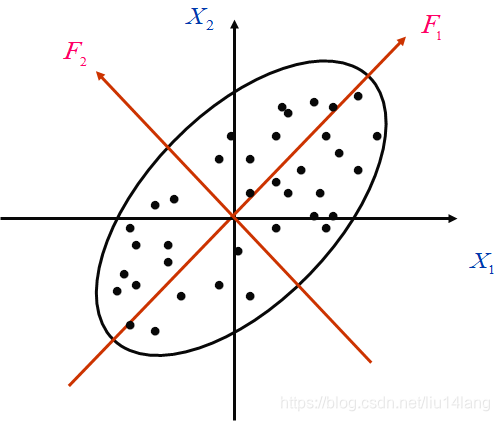
这时,由X1X_1X1和X2X_2X2的两个坐标轴构成了一个二维特征空间P1P_1P1。图上的黑点代表我们收集的样本,通过特征X1X_1X1和X2X_2X2表达在此图上,所以样本可以由空间P1P_1P1来描述。我们从图中可以看出X1X_1X1和X2X_2X2这两个特征对样本的描述影响程度差不多,貌似这两个特征缺一不可。
细心的同学已经发现了上图中还有F1F_1F1和F2F_2F2两个坐标轴,构成了另一个二维特征空间P2P_2P2,所以样本也可以由空间P2P_2P2描述。在空间P2P_2P2上,样本的F2F_2F2特征大多分布在一个比较小的范围内,有大量的样本的F2F_2F2值是相同的,不能很好的表示样本,相反F1F_1F1特征分布在一个比较大范围,大部分的y1值是不相等的,能够很好的表示样本。(这句话不好理解,可以这样想:如果只取F2F_2F2特征来描述样本发现很多样本是一样的,对样本表示的信息少,不好体现样本之间的差异;相反只取F1F_1F1特征来描述样本会发现大部分样本是不一样的,对样本表示的信息多,更好地体现样本之间的差异)。
恩~~~ 可以暂停思考一下。接下来我们取出所有样本的F1F_1F1值形成一个数列,并对其计算方差D1D_1D1,对F2F_2F2值也进行如此操作计算出D2D_2D2.我们可以通过比较D1D_1D1与D2D_2D2的大小,来决定特征F1F_1F1与F2F_2F2对样本影响程度(表示的信息)的大小,因为方差就是表示一组数据的离散程度,所以计算方差是合理的。当样本的特征空间为nnn时,我们也可以求出D=(D1,D2,...,Dn)D=(D_1,D_2,...,D_n)D=(D1,D2,...,Dn),对其进行排序,我们取出前mmm大的方差对应的特征来描述样本,这也是我们的主成分分析的思想。现在问题在于特征Y=(y1,y2,...,yn)Y=(y_1,y_2,...,y_n)Y=(y1,y2,...,yn)是如何求出来的。要是求出了YYY,问题也就迎刃而解了。
旋转变换
在求解YYY前,我们先来介绍下旋转变换。在图中,我们可以看出,空间P2P_2P2是可以通过空间P1P_1P1旋转变换得到的,并且这种坐标变换是正交变换的。变换公式如下:
[f1f2]=U′X+b=[cosθ−sinθsinθcosθ][x1x2]
\begin{bmatrix}f_1\\f_2\\\end{bmatrix}=U' X+b=\begin{bmatrix}cos\theta&-sin\theta\\sin\theta&cos\theta\\\end{bmatrix}\begin{bmatrix}x_1\\x_2\\\end{bmatrix}
[f1f2]=U′X+b=[cosθsinθ−sinθcosθ][x1x2]
其中U′=[cosθsinθ−sinθcosθ]U'=\begin{bmatrix}cos\theta&sin\theta\\-sin\theta&cos\theta\\\end{bmatrix}U′=[cosθ−sinθsinθcosθ]为旋转矩阵,并且是正交矩阵,即UU′=I,IUU'=I,IUU′=I,I称之为单位矩阵.[b122]\begin{bmatrix}b_1\\2_2\\\end{bmatrix}[b122]为位移矩阵。
主成分分析计算
变量假设
向量X=(x1,x2,...,xn)X=(x_1,x_2,...,x_n)X=(x1,x2,...,xn),其期望与协方差阵分别为μ=E(X),Σ=D(X)\mu=E(X),\Sigma=D(X)μ=E(X),Σ=D(X)
线性变换:yi=a1ix1+a2ix2+...+anixn=Ai′X,i=1,2,...my_i=a_{1i}x_1+a_{2i}x_2+...+a_{ni}x_n=A'_iX,i=1,2,...myi=a1ix1+a2ix2+...+anixn=Ai′X,i=1,2,...m
矩阵变换:Y=A′X,其中Y=(y1,y2,...,ym)′,A=(A1,A2,...,Am)Y=A'X,其中Y=(y_1,y_2,...,y_m)',A=(A_1,A_2,...,A_m)Y=A′X,其中Y=(y1,y2,...,ym)′,A=(A1,A2,...,Am)
算法步骤
(1)求解向量XXX的协方差Σ\SigmaΣ.
(2)求解Σ\SigmaΣ的特征值λ=(λ1,λ2,...,λm),其中λ1,λ2,...,λm都是Σ\lambda=(\lambda_1,\lambda_2,...,\lambda_m),其中\lambda_1,\lambda_2,...,\lambda_m都是\Sigmaλ=(λ1,λ2,...,λm),其中λ1,λ2,...,λm都是Σ矩阵的特征值,并且是依大至小排序。
(3)求解λi\lambda_iλi对应的单位化特征向量AiA_iAi.
(4)求解Yi=Ai′X,其中i=1,2,...,m。YiY_i=A'_iX,其中i=1,2,...,m。Y_iYi=Ai′X,其中i=1,2,...,m。Yi称为第iii主成分,其贡献率为ϕk=λk/∑k=1mλk\phi_k=\lambda_k/{\sum_{k=1}^m\lambda_k}ϕk=λk/∑k=1mλk,贡献率表示每个主成分对样本的表示程度,一般前几个主成分贡献率之和可以达到70%以上,故往后的主成分可以忽略。





















 1424
1424

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








