PTA_2019春_033_Tree Traversals Again

最新推荐文章于 2024-05-28 23:37:46 发布

原创最新推荐文章于 2024-05-28 23:37:46 发布

· 176 阅读

0 ·

版权

数据结构PTA 专栏收录该内容

26 篇文章

订阅专栏

该博客介绍了如何使用栈非递归地实现二叉树的中序遍历，并提供了一个具体的例子。给定一个6节点的二叉树及其对应的栈操作序列，任务是根据这些操作生成唯一的二叉树并输出其后序遍历序列。输入包含树的节点总数和一系列的栈操作，输出要求是相应二叉树的后序遍历序列。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

/*Tree Traversals Again */
/*思路：1.先将题中所给栈的步骤转化为树结构，然后对其进行后序遍历。
	2.感觉题目的本意是，给出中序遍历的出入栈操作，在这个基础上进行后序遍历非递归栈的实现。*/
/*2019/5/8 思路这么清晰的题目竟然也搞了挺久
           BUG竟然是我把\n 输成了/n 滑天下之大稽哉*/
#include<stdio.h> 
#include<stdlib.h>
#include<string.h>
typedef struct stackdata {
	char* operate;/*操作*/
	int num;        /*对象*/
	int label ;      /*标记，用于修改数组*/
}Stack;
/*树节点结构*/
typedef struct Treenode {
	int treedata;
	int right;
	int left;
	
}Tree;

/*后序，递归*/
void postordertraversal(int i,Tree * tree,int root);
int main() {
	int N;/*节点个数*/
	scanf("%d", &N);
	Stack* stack = (struct stackdata*)malloc(2 * N * sizeof(struct stackdata));
	for (int i = 0; i < 2 * N; i++) {
		stack[i].operate = (char*)malloc(5 * sizeof(char));
		scanf("%s", stack[i].operate);
		if (strlen(stack[i].operate)==4)  scanf("%d", &stack[i].num);
		else  stack[i].num = -1;
		stack[i].label=0;
	}/*输入完成*/

	/*下面修改结构体数组中 POP的NUM，为其输出的元素*/
	for (int i = 0; i < 2 * N; i++) {
		if (strlen(stack[i].operate) == 3) {   /*找到pop*/
			for (int j = i-1; j >= 0; j--) {
				if ((strlen(stack[j].operate) == 4) && stack[j].label == 0) { /*找到pop的对象*/
					stack[i].num = stack[j].num;
					stack[j].label = 1;/*标记已pop过*/
					break;
				}
			}
		}
	}/*修改结束*/

	/*下面创建原树，建树规则：遍历数组stack，若某元素的上一个为PUSH，则该元素为上一个元素的左子树
	                若上一个元素为POP则为上一个元素POP的元素的右子树*/
	Tree* tree = (struct Treenode*)malloc((N+1) * sizeof(struct Treenode)); /*用结构体数组表示树*/
	int root;  /*根节点*/ 
	for (int i = 1; i < N+1; i++) {
		tree[i].treedata=i;
		tree[i].left = -1;/*默认-1为空子节点*/
		tree[i].right = -1;
	}/*结构体初始化完成*/

    root = stack[0].num;
	for (int i = 1; i < 2 * N; i++) {
		if (strlen(stack[i].operate) == 4) {  /*找PUSH*/
			if (strlen(stack[i - 1].operate) == 4) {   /*上一个为PUSH，则当前的节点为上一个节点的左子树*/
			    
				tree[stack[i-1].num].left = stack[i].num;
			}
			else{                                    /*上一个为POP，则它为上一个POP对像的右子树*/
				tree[stack[i-1].num].right = stack[i].num;
			}
		}
	}/*建树完成*/        
	
	/*后序遍历树，递归*/
	postordertraversal(root, tree,root);
	return 0;
}
void postordertraversal(int i,Tree * tree,int root) {
	if (i != -1) {
		postordertraversal(tree[i].left,tree,root);
		postordertraversal(tree[i].right,tree,root);
		printf("%d", tree[i].treedata);
		if(i!=root) printf(" ");
	}
}

An inorder binary tree traversal can be implemented in a non-recursive way with a stack. For example, suppose that when a 6-node binary tree (with the keys numbered from 1 to 6) is traversed, the stack operations are: push(1); push(2); push(3); pop(); pop(); push(4); pop(); pop(); push(5); push(6); pop(); pop(). Then a unique binary tree (shown in Figure 1) can be generated from this sequence of operations. Your task is to give the postorder traversal sequence of this tree.

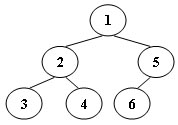
Figure 1

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive integer N (≤30) which is the total number of nodes in a tree (and hence the nodes are numbered from 1 to N). Then 2N lines follow, each describes a stack operation in the format: "Push X" where X is the index of the node being pushed onto the stack; or "Pop" meaning to pop one node from the stack.

Output Specification:

For each test case, print the postorder traversal sequence of the corresponding tree in one line. A solution is guaranteed to exist. All the numbers must be separated by exactly one space, and there must be no extra space at the end of the line.

Sample Input:

6
Push 1
Push 2
Push 3
Pop
Pop
Push 4
Pop
Pop
Push 5
Push 6
Pop
Pop

Sample Output:

3 4 2 6 5 1