DH 密钥交换原理

假设 q 为素数，对于正整数 a,x,y，有：

(a^x mod p)^y mod p = a^(xy) mod p

证明如下：

令 a^x = mp + n， 其中 m, n 为自然数， 0 <= n < p，则有
C = (a^x mod p)^y mod p
  = ((mp + n) mod p)^y mod p
  = n^y mod p
  = (mp +n)^y mod p
  = a^(xy) mod p

由于 xy = yx 所以公式可以变形为：

(a^x mod p)^y mod p = (a^y mod p)^x mod p = password

我们把 a^x mod p 记作 Ka，把 a^y mod p 记做 Kb

此时如果 Alice 和 Bob 在公网中，对 Ka，Kb，a，和 p 达成一致。Alice 持有 x 作为私有的，Bob 持有 y 作为私有的。双方都能计算出 password ，而无法知道对方实际持有的 x 和 y。只要 x，y 足够大，公网中传输的数据，也很难计算出 password

加密强度保证：（有限群的离散对数问题） 对于 a^x mod p = Ka , p很大时，由 Ka 和 p、a 很难计算出 x

如图：

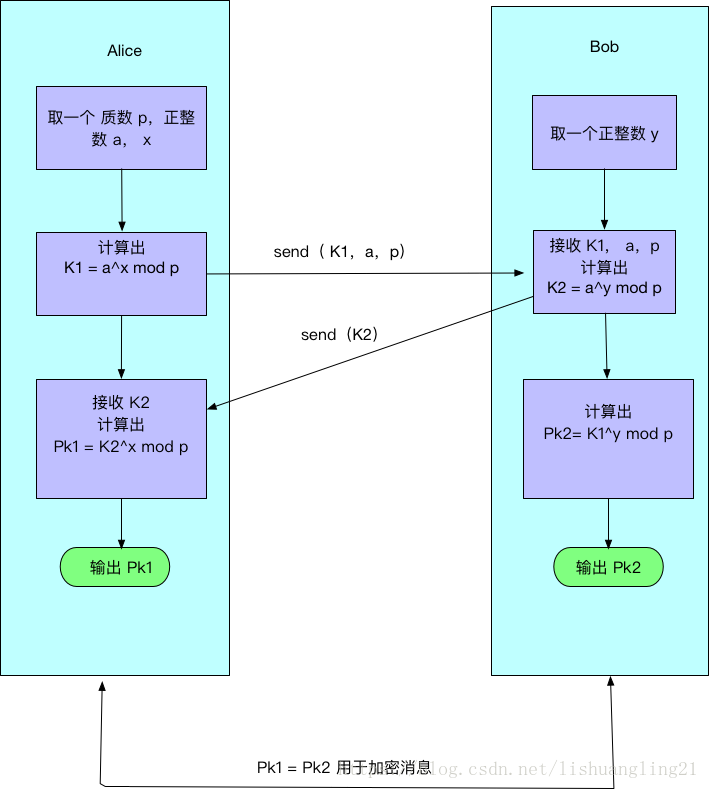
DH 无法防止中间人攻击

可能导致的现象： 攻击者假冒身份，和两边分别建立 DH，就可以实现中间人攻击了。